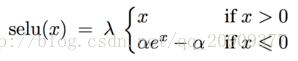深度前饋網路又稱多層感知機、前饋神經網路。即只有從x向y方向的傳播，最終輸出y。

主要包括輸入層、隱藏層和輸出層。神經網路的模型可以解決非線性問題。

計算網路的引數通過反向傳播；如果每一層隱藏層都只有wx+b的運算，則多層累加變為w1*(w2*(w3*x))+a = W*x +a,失去了非線效能力。故每一層後面會加上一個啟用層。

例項：學習XOR

單個線性函式無法解決XOR的問題，但是多個線性函式的組合，每個線性函式理解為一個神經元，就可以表示XOR運算。

這裡提到了RELU啟用函式g(x) = max{0,x}，也叫整流線性單元，是大多前饋神經網路的預設啟用函式。主要優勢運算簡單。後面有專門章節介紹和比較各個啟用函式。

基於梯度的學習：

代價函式：和其他機器學習使用方式類似。

使用最大似然學習條件分佈：

學習條件統計量：

輸出單元：

主要就是sigmoid 和softmax兩種,都存在飽和的問題，前者在輸入過大和過小時，後者在有某個預測特別大時。

sigmoid：主要用於二分類，或輸出概率。 這邊提到softplus:ζ(x)=ln(1+exp(x))

softmax：

輸出每個類可能的概率。多分類以及預測自然語言處理中預測下一句話之類時可以用到。但是如果可能性太多的話，運算過大，可以通過樹狀結構減少運算。

隱藏單元：

隱藏單元主要包括仿射變換 wx+b 和啟用函式g(x)，重點研究啟用函式：

下面介紹幾種常見啟用函式：

ReLU族

ReLU：整流線性單元 g(z0) = max(0,z)，最常用。

優勢：計算方便，大於0部分不存在梯度飽和。

計算時通常將仿射變換的b初始設定一個較小的正數，如0.1，這樣開始時大多數樣本都可以通過。

缺點：無法學習小於0的樣本。

針對上述缺點出現了很多變種：

LeakReLU:

這樣可以學習小於0的部分。

PReLU:同LeakReLU，但是a引數是根據資料確定的，而非事先指定

學習方式如下：

RReLU:

RReLU:訓練時是波動的，測試時就固定下來了。

ELU:

SReLU:

啟用後樣本均值為0，方差為1，相當於自歸一化，效果比batchnormlize好。

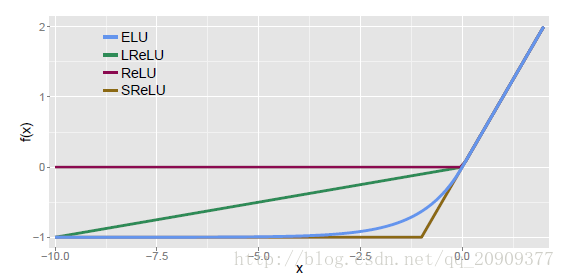
參考別人的一幅圖再。

補充一個softplus:

ζ(x)=ln(1+exp(x)):

softplus相當於平滑版的ReLU。

再回憶一下這些啟用函式的性質：

Sigmoid族

在整流線性單元之前，主要使用Sigmoid啟用函式和tanh啟用函式

Sigmoid:

將實數壓縮到0到1，適用於輸出概率

導數

tanh:g(z) = tanh(z) = 2(2z)-1

將實數壓縮到-1到1

導數

sigmoid函式容易飽和，不適合前饋神經網路中隱藏層的啟用。但是在諸如LSTM的網路中有用。

二分類問題，一般隱藏層用tanh。因為其均值為0，保持整個網路始終輸入0均值的資料，較易優化。

其他都不常用了。也沒有什麼優勢就不介紹了。

架構設計：

理論上深度學習網路可以近似實數空間中的所有函式，只要神經元足夠多。

深度學習之所以優越，就是因為同等的表達能力，深層網路需要的神經元小於淺層網路且相對不容易過擬合。

深度網路不單單是一層層的依次連結，後面章節會有介紹多種變種的深度學習網路。

反向傳播和其他的微分演算法：

從x到y時前向傳播，產生一個標量代價函式：

反過來從y計算梯度調整引數稱為反向傳播。

通過計算圖來看資料流向：

主要通過鏈式法則計算。

這裡花書的略深奧了，看了bilibili的一篇視訊很不錯，連結如下：

大概的意思如下：

反向傳播是一層層傳播的，比如最後一層往倒數第二層傳播，而後第二層繼續往第三層傳播。不是像我之前一個同事理解的，先計算最後一層相對倒數第二層的偏導，然後計算最後一層相對倒數第三層的偏導，即每次都是最後一層往上傳播，這個是不對的。

我們可以理解最後一層的輸出為,這個是經過神經網路後最後得到的輸出。而實際的輸出為y。那麼這裡的誤差就是,我們設他為Z。這裡的Z是輸出層所有輸出和預期的均方差之和。即：

這個是怎麼來的呢，就是經過前面一層所有的權重相乘後相加再加上偏移獲得：

這裡a1表示前一層和w1對應的那個權重在上一層得到的啟用值。

得到前面的Z，而後即可針對w,a,以及b分別求他們的偏導，更新他們的新的值。w和b更新為新的值，a的值可以認為是上一層的預期輸出，其差值正好可以作為再上一層的均方誤差進行訓練。

這裡每一次更新不是一個樣本，而是一個打亂的小批次，這就是隨機梯度下降。

這就是根據自己理解的反向傳播演算法了。