資料結構之排序
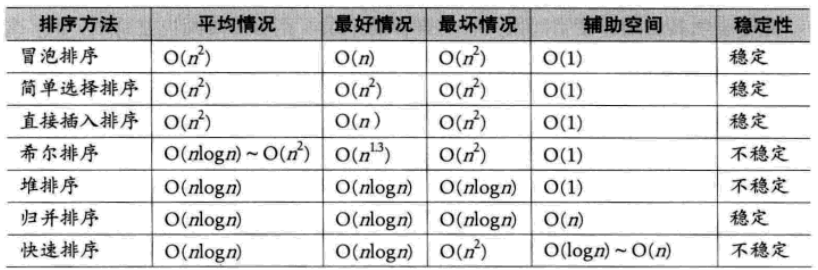
內排序是在排序整個過程中,待排序的所有記錄全部被放置在記憶體中。外排序是由於排序的記錄個數太多,不能同時放置在記憶體中,整個排序過程需要在內外存之間多次交換資料才能進行。這裡我們介紹內排序的幾種方法。

排序用到的資料結構:
#define MAXSIZE 10
/*定義順序表*/
typedef struct
{
int r[MAXSIZE+1];
int length;
}SqList;
/*交換L中陣列的值*/
void swap(SqList *L, int i, int j)
{
int temp=L->r[i];
L->r[i]=L->r[j];
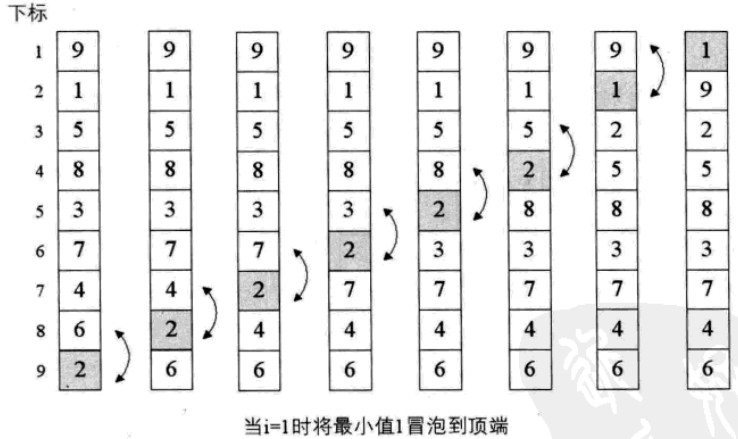
L->r[ 氣泡排序
- i=1:L->length,i++
- j=L->length-1:i,j–
- 若L->r[j]大於L->r[j+1],交換swap(L, j, j+1);
void BubbleSort(SqList *L)
{
int i,j;
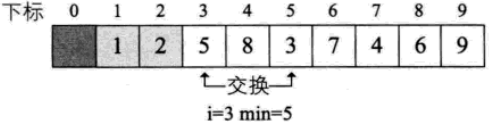
for(i=1;i<L->length; 選擇排序
i=1:L->length,每次選取最小的值填入L[i]。
void SelectSort(SqList *L)
{
int i,j,min;
for(i=1;i<L->length; 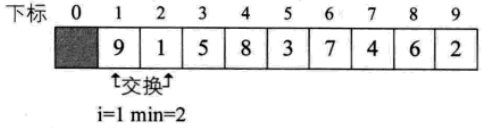
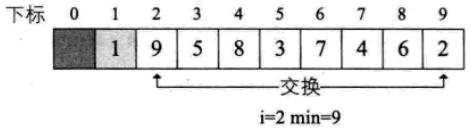
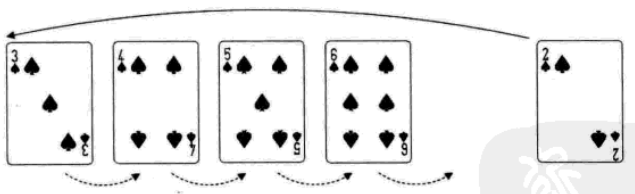
插入排序
將一個記錄插入到已經排好序的有序表中,從而得到一個新的、記錄數增1的有序表。
void InsertSort(SqList *L)
{
int i,j;
for(i=2;i<=L->length;i++)
{
if (L->r[i]<L->r[i-1]) /* 需將L->r[i]插入有序子表 */
{
L->r[0]=L->r[i]; /* 設定哨兵 */
for(j=i-1;L->r[j]>L->r[0];j--)
L->r[j+1]=L->r[j]; /* 記錄後移 */
L->r[j+1]=L->r[0]; /* 插入到正確位置 */
}
}
}
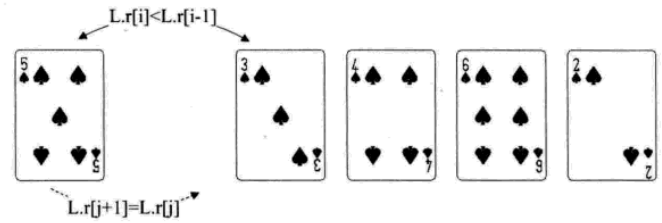
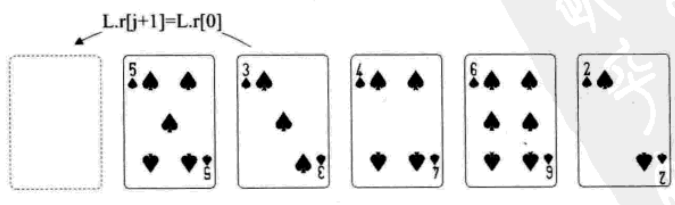
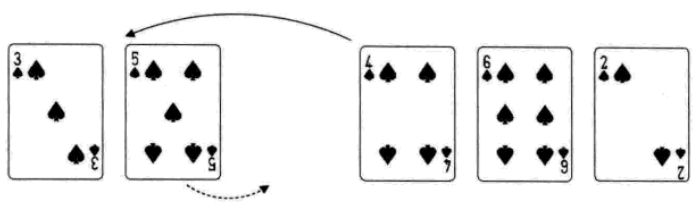
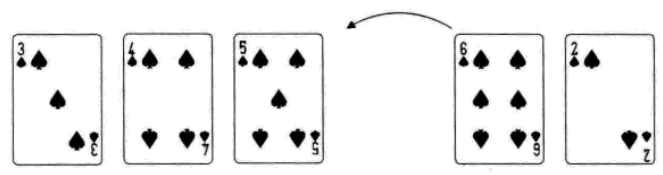
希爾排序
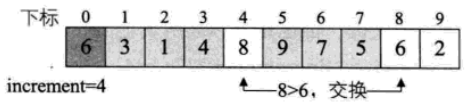
1. 增量:increment = increment/3+1=9/3+1=4;increament初始化為陣列長度9。
2. i=increment+1:L->length;比較L.r[i-increment]與L.r[i]的大小,把較小(大)值換到前面。

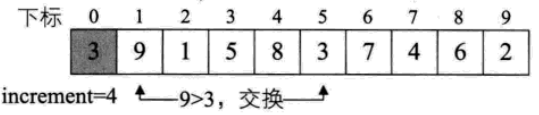
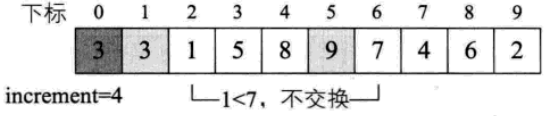
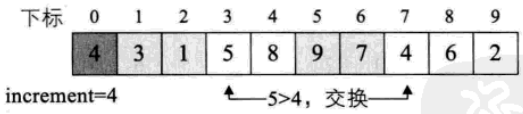
3. 當i-increment>increment時,還需要比較L.r[i-increment*2]與L.r[i]的大小。
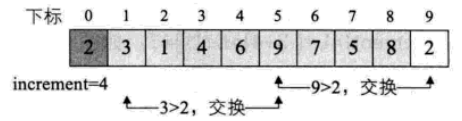
經過第一輪迴圈,陣列已經基本有序。

4. increment=increment/3+1=4/2+1=3,繼續迴圈。
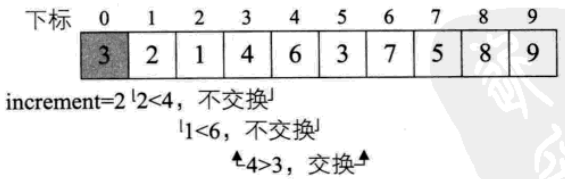
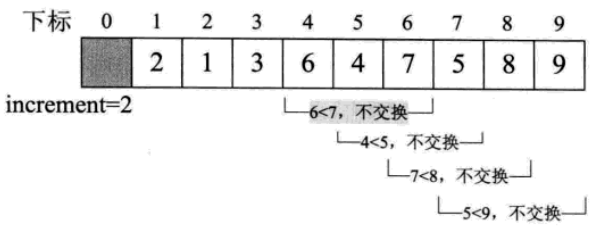
5. increment=increment/3+1=3/3+1=2,繼續迴圈。
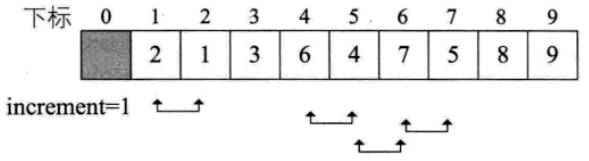
void ShellSort(SqList *L)
{
int i,j,k=0;
int increment=L->length;
do
{
increment=increment/3+1;/* 增量序列 */
for(i=increment+1;i<=L->length;i++)
{
if (L->r[i]<L->r[i-increment])/* 需將L->r[i]插入有序增量子表 */
{
L->r[0]=L->r[i]; /* 暫存在L->r[0] */
for(j=i-increment;j>0 && L->r[0]<L->r[j];j-=increment)
L->r[j+increment]=L->r[j]; /* 記錄後移,查詢插入位置 */
L->r[j+increment]=L->r[0]; /* 插入 */
}
}
printf(" 第%d趟排序結果: ",++k);
print(*L);
}while(increment>1);
}
堆排序
堆是具有下列性質的完全二叉樹:每個結點的值都大於或等於其左右孩子結點的值,稱為大項堆;或者每個結點的值都小於或者等於其左右孩子結點的值,稱為小項堆。
堆排序:
- 構造大項堆
- 將根結點(
最大值)與陣列末尾元素交換 - 然後剔除最大值(末尾結點),將剩餘序列重新構造成一個大項堆,得到
次小值 - 反覆執行,得到排序序列
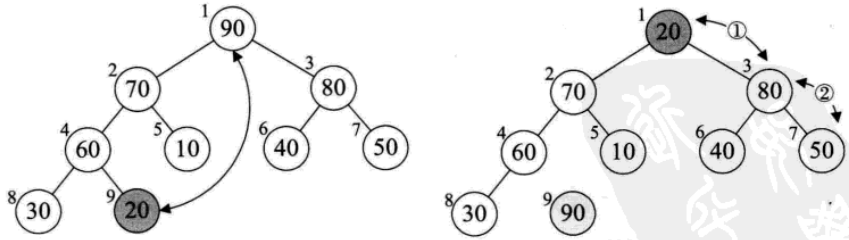
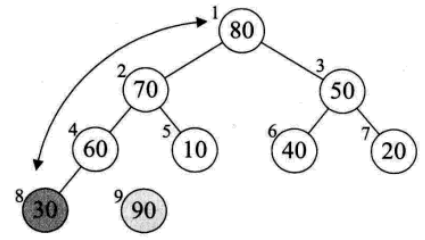
(1)i從4:1,因為1,2,3,4是有孩子的結點,將這些結點的子樹也構成大項堆(2)當前結點序號s,其左孩子一定是2s,右孩子一定是2s+1(二叉樹性質5)(3)通過比較結點和左右子樹的大小,保持結點數大於左右子樹(4)交換根結點與最後元素並剔除最大值後,重新構建大項堆
/* 已知L->r[s..m]中記錄的關鍵字除L->r[s]之外均滿足堆的定義, */
/* 本函式調整L->r[s]的關鍵字,使L->r[s..m]成為一個大頂堆 */
void HeapAdjust(SqList *L,int s,int m)
{
int temp,j;
temp=L->r[s];
for(j=2*s;j<=m;j*=2) /* 沿關鍵字較大的孩子結點向下篩選 */
{
if(j<m && L->r[j]<L->r[j+1])
++j; /* j為關鍵字中較大的記錄的下標 */
if(temp>=L->r[j])
break; /* rc應插入在位置s上 */
L->r[s]=L->r[j];
s=j;
}
L->r[s]=temp; /* 插入 */
}
/* 對順序表L進行堆排序 */
void HeapSort(SqList *L)
{
int i;
for(i=L->length/2;i>0;i--) /* 把L中的r構建成一個大根堆 */
HeapAdjust(L,i,L->length);
for(i=L->length;i>1;i--)
{
swap(L,1,i); /* 將堆頂記錄和當前未經排序子序列的最後一個記錄交換 */
HeapAdjust(L,1,i-1); /* 將L->r[1..i-1]重新調整為大根堆 */
}
}
歸併排序
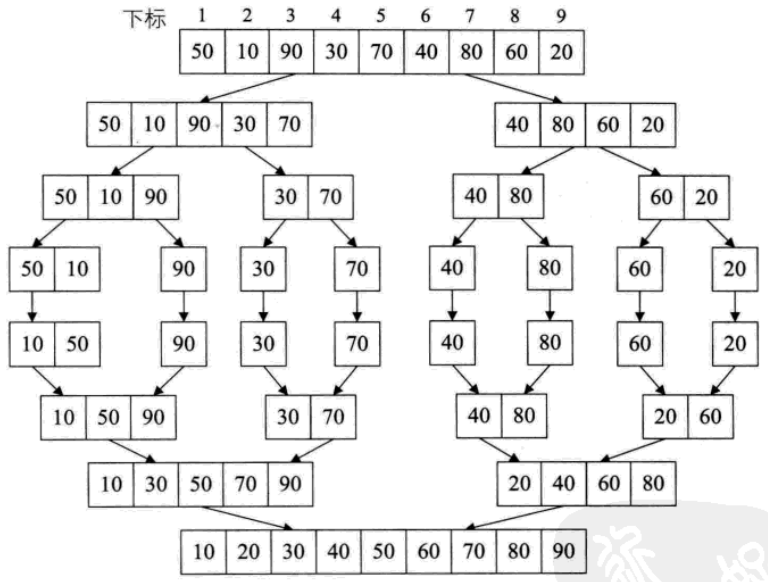
將長度為n的序列分解成n/1個長度為2或1的子序列,然後兩兩歸併,最終得到長度為n的有序序列為止。
void Merge(int SR[],int TR[],int i,int m,int n)
{
int j,k,l;
for(j=m+1,k=i;i<=m && j<=n;k++) /* 將SR中記錄由小到大地併入TR */
{
if (SR[i]<SR[j])
TR[k]=SR[i++];
else
TR[k]=SR[j++];
}
if(i<=m)
{
for(l=0;l<=m-i;l++)
TR[k+l]=SR[i+l]; /* 將剩餘的SR[i..m]複製到TR */
}
if(j<=n)
{
for(l=0;l<=n-j;l++)
TR[k+l]=SR[j+l]; /* 將剩餘的SR[j..n]複製到TR */
}
}
/* 遞迴法 */
/* 將SR[s..t]歸併排序為TR1[s..t] */
void MSort(int SR[],int TR1[],int s, int t)
{
int m;
int TR2[MAXSIZE+1];
if(s==t)
TR1[s]=SR[s];
else
{
m=(s+t)/2; /* 將SR[s..t]平分為SR[s..m]和SR[m+1..t] */
MSort(SR,TR2,s,m); /* 遞迴地將SR[s..m]歸併為有序的TR2[s..m] */
MSort(SR,TR2,m+1,t); /* 遞迴地將SR[m+1..t]歸併為有序的TR2[m+1..t] */
Merge(TR2,TR1,s,m,t); /* 將TR2[s..m]和TR2[m+1..t]歸併到TR1[s..t] */
}
}
/* 對順序表L作歸併排序 */
void MergeSort(SqList *L)
{
MSort(L->r,L->r,1,L->length);
}
歸併排序大量引用了遞迴,儘管在程式碼上比較清晰,容易理解,但這會造成時間和空間上的效能損耗,下面採用迭代的方法實現歸併排序:
void MergePass(int SR[],int TR[],int s,int n)
{
int i=1;
int j;
while(i <= n-2*s+1)
{/* 兩兩歸併 */
Merge(SR,TR,i,i+s-1,i+2*s-1);
i=i+2*s;
}
if(i<n-s+1) /* 歸併最後兩個序列 */
Merge(SR,TR,i,i+s-1,n);
else /* 若最後只剩下單個子序列 */
for(j =i;j <= n;j++)
TR[j] = SR[j];
}
/* 對順序表L作歸併非遞迴排序 */
void MergeSort2(SqList *L)
{
int* TR=(int*)malloc(L->length * sizeof(int));/* 申請額外空間 */
int k=1;
while(k<L->length)
{
MergePass(L->r,TR,k,L->length);
k=2*k;/* 子序列長度加倍 */
MergePass(TR,L->r,k,L->length);
k=2*k;/* 子序列長度加倍 */
}
}
快速排序
快速排序的基本思想是:通過一趟排序,使得序列分成兩部分,一部分關鍵字均比另一部分小,則可分別對這兩子序列繼續排序。
Partition函式要做的是選取一個關鍵字,比如50,想盡辦法給他安排一個位置,使得他的左邊都比他小,右邊都比他大,稱這個關鍵字為樞軸。比如序列{50,10,90,30,70,40,80,60,20},50為樞軸,變換為{20,10,40,30,50,70,80,60,90}。
1. 20比樞軸小,交換,使20在樞軸左邊,low++
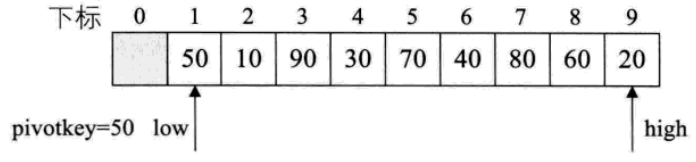
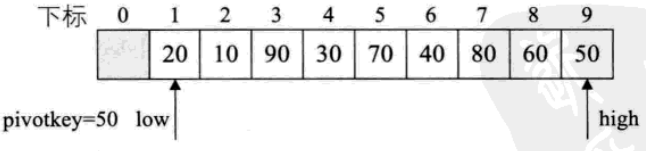
2. 90比樞軸大,交換,high--
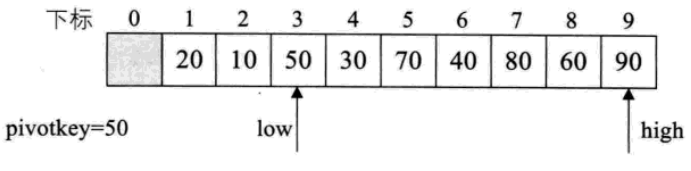
3. 直到high指向40,比樞軸小,交換,low++
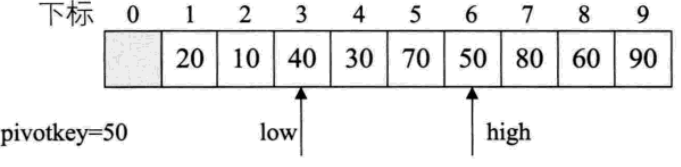
4. 遇到70比樞軸大,交換,high--
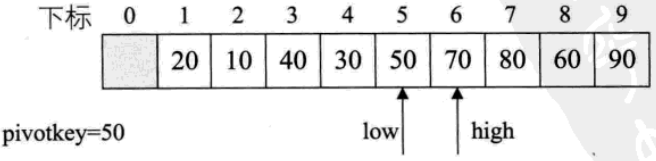
5. low=high=5,第一輪排序結束。
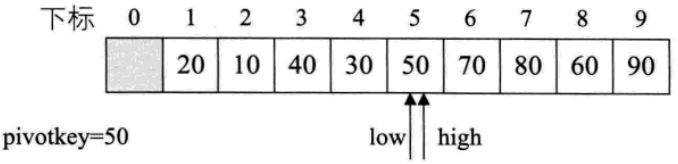
6. 再分別對樞軸兩邊的子序列進行排序。
/* 交換順序表L中子表的記錄,使樞軸記錄到位,並返回其所在位置 */
/* 此時在它之前(後)的記錄均不大(小)於它。 */
int Partition(SqList *L,int low,int high)
{
int pivotkey;
pivotkey=L->r[low]; /* 用子表的第一個記錄作樞軸記錄 */
while(low<high) /* 從表的兩端交替地向中間掃描 */
{
while(low<high&&L->r[high]>=pivotkey)
high--;
swap(L,low,high);/* 將比樞軸記錄小的記錄交換到低端 */
while(low<high&&L->r[low]<=pivotkey)
low++;
swap(L,low,high);/* 將比樞軸記錄大的記錄交換到高階 */
}
return low; /* 返回樞軸所在位置 */
}
/* 對順序表L中的子序列L->r[low..high]作快速排序 */
void QSort(SqList *L,int low,int high)
{
int pivot;
if(low<high)
{
pivot=Partition(L,low,high); /* 將L->r[low..high]一分為二,算出樞軸值pivot */
QSort(L,low,pivot-1); /* 對低子表遞迴排序 */
QSort(L,pivot+1,high); /* 對高子表遞迴排序 */
}
}
/* 對順序表L作快速排序 */
void QuickSort(SqList *L)
{
QSort(L,1,L->length);
}
快速排序優化
- 優化樞軸:樞軸的選取可採用隨機數、三個數排序取中間值、九數排序取中等方法。
- 優化不必要的交換:將樞軸放在r[0]處,將元素交換改成替換。
- 優化小陣列的排序:設定閾值,小陣列採用插入排序。
- 優化遞迴:將兩個遞迴(高、低子表遞迴排序)簡化為一個遞迴操作+while迴圈。
/* 快速排序優化演算法 */
int Partition1(SqList *L,int low,int high)
{
int pivotkey;
int m = low + (high - low) / 2; /* 計算陣列中間的元素的下標 */
if (L->r[low]>L->r[high])
swap(L,low,high); /* 交換左端與右端資料,保證左端較小 */
if (L->r[m]>L->r[high])
swap(L,high,m); /* 交換中間與右端資料,保證中間較小 */
if (L->r[m]>L->r[low])
swap(L,m,low); /* 交換中間與左端資料,保證左端較小 */
pivotkey=L->r[low]; /* 用子表的第一個記錄作樞軸記錄 */
L->r[0]=pivotkey; /* 將樞軸關鍵字備份到L->r[0] */
while(low<high) /* 從表的兩端交替地向中間掃描 */
{
while(low<high&&L->r[high]>=pivotkey)
high--;
L->r[low]=L->r[high];
while(low<high&&L->r[low]<=pivotkey)
low++;
L->r[high]=L->r[low];
}
L->r[low]=L->r[0];
return low; /* 返回樞軸所在位置 */
}
void QSort1(SqList *L,int low,int high)
{
int pivot;
if((high-low
相關推薦
資料結構之排序演算法(五)
// 索引堆
function swap(arr, x, y) { var temp = arr[x];
資料結構之排序篇——選擇排序 //交換第i下標與最小下標,只交換一次
首先在陣列的所有元素中找到一個最小的元素,
將該元素與陣列的第一個元素進行交換,
這樣交換之後,陣列的第一個元素就變成了陣列元素中的最小值,
再在除第一個元素外的其它陣列元素中,尋找最小的陣列元素,
將這個第二小的陣列元素與陣列
資料結構之排序篇——插入排序 //無序查詢有序位置,邊比較邊移動,有哨兵
typedef int DataType; void insert(DataType *a, int n) { for (int i = 1; i < n; i++) {
資料結構之排序篇——氣泡排序 //逆序則交換
typedef int DataType; void bubble(DataType* a, int n) { for (int i = 0; i < n - 1; i++) {
資料結構之排序演算法
JavaScript實現排序演算法
程式碼實現
const ArrayList = function() {
let array = [],
length = 0;
this.insert = function(item) {
資料結構之排序
內排序是在排序整個過程中,待排序的所有記錄全部被放置在記憶體中。外排序是由於排序的記錄個數太多,不能同時放置在記憶體中,整個排序過程需要在內外存之間多次交換資料才能進行。這裡我們介紹內排序的幾種方法。
排序用到的資料結構:
#define MAXSIZE 1
資料結構之排序篇——插入排序 //無序查詢有序位置,邊比較邊移動,有哨兵
typedef int DataType;
void insert(DataType *a, int n) {
for (int i = 1; i < n; i++) {
//把選擇的元素放在臨時變數中
Da
資料結構之排序演算法(五)-直接插入排序,希爾排序,直接選擇排序
直接插入排序:時間複雜度:O(n^2)
基本演算法思路是:把後面待排序的記錄按其關鍵字的大小逐個插入到一個已經排好序的有序序列中,直到所有記錄插完為止,得到一個新的有序序列。(無序插入前面有序)
演算
資料結構之排序(七)——歸併排序
歸併排序(Merging Sort):假設初始序列含有n個記錄,則可以看成是n個有序的子序列,每個子序列的長度為1,然後倆倆歸併,得到[n/2]([x]表示不小於x的最小整數)個長度為2或1的有序子序列;再倆倆歸併,....,如此重複,直至得到一個長度為n的有序序列為止,這
走進資料結構之排序(一)---直接插入排序
一、直接插入排序演算法分析
直接插入排序是假定前i個構成的子序列是處於已排序的情況下進行排序的,然後將第i個元素與前i個構成的子序列逆序進行比較,如果是要升序排序,則比較第i個元素是否比j=i-1(i-1需要>=0)的元素大,如果是則第i個元素的位置(即j+1的位置上
演算法與資料結構之排序演算法的相關知識,簡單易懂。
一、 氣泡排序
1) 概要
本章介紹排序演算法中的氣泡排序,重點講解氣泡排序的思想。
目錄
1. 氣泡排序介紹
2. 氣泡排序圖文說明
3. 氣泡排序的時間複雜度和穩定性
4. 氣泡排序實現
4.1 氣泡排序C實現
4.2 氣泡排序C++實現
4.
資料結構之排序:歸併排序
歸併排序(Merging Sort)是與插入排序、交換排序、選擇排序不同的另一類排序方法。歸併的含義時將兩個(二路歸併)或兩個以上(多路歸併)的有序表合併成一個新的有序表。此處只討論二路歸併。
基本思想
將待排序序列r[0]到r[n-1]看成是一個含有n個長
資料結構之排序(未完,待續)
//資料結構知識點總結
//插入排序
//主程式碼
#include<stdio.h>
void InsertSort(int * a, size_t n)//直接插入排序
{
assert(a != NULL);
int end =
排序演算法之選擇排序(關鍵詞:資料結構/演算法/排序演算法/選擇排序)
假定:有 1 個亂序的數列 nums ,其中有 n 個數。 要求:排好序之後是 從小到大 的順序。
選擇排序演算法
程式碼
from swap import swap
def select_sort(nums):
n = len(nums)
i = 0
while
排序演算法之插入排序(關鍵詞:資料結構/演算法/排序演算法/插入排序)
假定:有 1 個亂序的數列 nums ,其中有 n 個數。 要求:排好序之後是 從小到大 的順序。
插入排序演算法
程式碼
def insert_sort(nums):
i = 1
n = len(nums)
while i <= n-1:
j = i
排序演算法之氣泡排序(關鍵詞:資料結構/演算法/排序演算法/氣泡排序)
假定:有 1 個亂序的數列 nums ,其中有 n 個數。 要求:排好序之後是 從小到大 的順序。
氣泡排序演算法
程式碼
from swap import swap
def bubble_sort(nums):
n = len(nums)
for i in rang
資料結構之拓撲排序和關鍵路徑
拓撲排序
在一個表示工程的有向圖中,用頂點表示活動,用弧表示活動之間的優先關係,這樣的有向圖為頂點表示活動的網,稱為AOV網。 基本思路:從AOV網中選擇一個入度為0的頂點輸出,然後刪去此頂點,並刪除以此頂點為尾的弧,繼續重複此步驟,直到輸出全部頂點或者AOV網中不存在入度為0的頂
資料結構之氣泡排序
氣泡排序是一種極其簡單的排序演算法,也是我所學的第一個排序演算法。它重複地走訪過要排序的元素,依次比較相鄰兩個元素,如果他們的順序錯誤就把他們調換過來,直到沒有元素再需要交換,排序完成。這個演算法的名字由來是因為越小(或越大)的元素會經由交換慢慢“浮”到數列的頂端。
氣泡排序演算法的運作如下
資料結構之內部排序--希爾排序
概要
-IDE:Pycharm -Python版本:python3.x -演算法分類:內部排序->插入類排序->希爾排序
演算法思想
希爾排序又稱縮小增量排序法,是一種基於插入思想的排序方法。它利用了直接插入排序的最佳性質,首先,將待排序的關鍵字序列分成若干個較小的序列,對子序列進行直接的插
資料結構之內部排序--直接插入排序
概要
-IDE:Pycharm -Python版本:python3.x -演算法分類:內部排序->插入類排序->直接插入排序
演算法思想
直接插入排序是一種最基本的插入排序方法,其基本操作是將第$i$個記錄插到前面$i-1$個記錄中。然後將大於自身的記錄從後往前依次向後移一位. 例如:將第$