p1173 最大連續和

題目

描述 Description
給定N個數，求這N(1 <=N <= 100,000) 個數的某個連續子序列的累加和，保證這個連續子序列的累加和最大。
輸入格式 Input Format
第一行：一個整數N。(1 <=N <= 100,000)
接下來N行，每行一個整數P_i(-1,000 <= P_i <= 1,000)。表示第i個數。
輸出格式 Output Format
一個整數，表示子序列的最大連續累加和。
樣例輸入 Sample Input

7
-3
4
9
-2
-5
8
-3
樣例輸出 Sample Output

14
時間限制 Time Limitation
1s
註釋 Hint
(4, 9, -2, -5, 8) => 14.
子序列不能為空！！
來源 Source
usaco 2011 Jan

程式碼

#include<bits/stdc++.h>
using namespace std;
int a[100000];
int main()
{
	int n;
	cin>>n;
	int maxnum=-220000;
	int sum=0;
	for (int i=0;i<n;i++)
	{
		cin>>a[i];
		sum+=a[i];
		if (sum>maxnum) maxnum=sum;
		if (sum<0) sum=0;
	}
	cout<<maxnum<<endl;
	return 0;
}

p1174 最大連續子矩陣累加和

題目

描述 Description
給定一個正整數n（ n<=500），然後輸入一個N*N矩陣。求矩陣中最大加權矩形，即矩陣的每一個元素都有一權值，權值定義在整數集上。從中找一矩形，矩形大小無限制，是其中包含的所有元素的和最大 。矩陣的每個元素屬於[-1100,1100]
例：
0 –2 –7 0　　　　　　 在左下角： 9 2
9 2 –6 2　　　　　　　　　　　　-4 1　　
-4 1 –4 1　　　　　　　　　　 -1 8
-1 8 0 –2　　　　　　　　　　 和為15
輸入格式 Input Format
第一行：n，
接下來是n行n列的矩陣。
輸出格式 Output Format
一個整數，表示最大子矩陣的和。
樣例輸入 Sample Input

4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2

樣例輸出 Sample Output

15
時間限制 Time Limitation
1s
註釋 Hint
經典問題，考慮如何降維。
來源 Source
經典問題。
POJ1050

程式碼

#include<bits/stdc++.h>
using namespace std;
int sum[510][510];
int n,maxnum=-200000,temp[51000];
void init()
{
	scanf("%d",&n);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			scanf("%d",&sum[i][j]);
	for (int i=1;i<=n;i++)
		for (int j=1;j<=n;j++)
			sum[i][j]+=sum[i-1][j];//sum[i][j]表示第i列,前j行的累加和
}
void work()
{
	memset(temp,-1,sizeof(temp)); 
	for (int i=1;i<=n;i++)
		for (int j=1;j<=i;j++)
		{//temp[k]表示第k列從第i行到第j行的累加和
			for (int k=1;k<=n;k++) 
				temp[k]=sum[i][k]-sum[j-1][k];
			int s=0;
			for (int k=1;k<=n;k++)
			{
				s+=temp[k];
				if (s>maxnum) maxnum=s;
				if (s<0) s=0;
			}
		}	
}
void printf()
{
	cout<<maxnum<<endl;
}
int main()
{
	init();
	work();
	printf();		
	return 0;
}

p1164 立方體求和

題目

描述 Description
SubRaY有一天得到一塊西瓜,是長方體形的…
SubRaY發現這塊西瓜長m釐米,寬n釐米,高h釐米.他發現如果把這塊西瓜平均地分成mnh塊1立方厘米的小正方體,那麼每一小塊都會有一個營養值(可能為負,因為西瓜是有可能壞掉的,但是絕對值不超過200).
現在SubRaY決定從這mnh立方厘米的西瓜中切出mmnnhh立方厘米的一塊小西瓜(一定是立方體形,長寬高均為整數),然後吃掉它.他想知道他最多能獲得多少營養值.(0<=mm<=m,0<=nn<=n,0<=hh<=h.mm,nn,hh的值由您來決定).
換句話說,我們希望從一個mnh的三維矩陣中,找出一個三維子矩陣,這個子矩陣的權和最大.

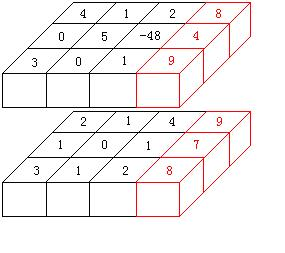
一個234的例子,最優方案為切紅色231部分
輸入格式 Input Format
首行三個數h,m,n(注意順序),分別表示西瓜的高,長,寬.
以下h部分,每部分是一個m*n的矩陣,第i部分第j行的第k個數表示西瓜第i層,第j行第k列的那塊1立方厘米的小正方體的營養值.
輸出格式 Output Format
SubRaY所能得到的最大營養值
樣例輸入 Sample Input

2 3 4
4 1 2 8
0 5 -48 4
3 0 1 9
2 1 4 9
1 0 1 7
3 1 2 8

樣例輸出 Sample Output

45
時間限制 Time Limitation
1s
註釋 Hint
對於30%的資料,h=1,1<=m,n<=10
對於全部的資料,1<=h<=32,1<=m,n<=50,保證h<=m,n

程式碼

#include<bits/stdc++.h>
#include<algorithm>
using namespace std;
int a[101][101][101],b[101][101],c[101],s,maxnum=-20000;
int main()
{
	memset(c,0,sizeof(c));
	int h,m,n;
	scanf("%d %d %d",&h,&m,&n);
	for (int i=1;i<=h;i++)
		for (int j=1;j<=m;j++)
			for (int k=1;k<=n;k++)
			{
				scanf("%d",&a[i][j][k]);
				a[i][j][k]+=a[i-1][j][k];
			}
	
	for (int i=1;i<=h;i++)
		for (int j=i;j<=h;j++)
		{
			for (int k=1;k<=m;k++)
				for (int l=1;l<=n;l++)
				{
					b[k][l]=a[j][k][l]-a[i-1][k][l];
					b[k][l]+=b[k][l-1];
				}
			
			for (int k=1;k<=n;k++)
				for (int l=k;l<=n;l++)
				{
					s=0;
					for (int x=1;x<=m;x++)
					{
						c[x]=b[x][l]-b[x][k-1];
						s+=c[x];
						if (s>maxnum) maxnum=s;
						if (s<0) s=0;
					}	
				}
		}
	printf("%d\n",maxnum);
	return 0;
}