Android PriorityQueue和PriorityBlockingQueue原始碼解析
阿新 • • 發佈:2018-12-12
尊重原創,轉載請標明出處 http://blog.csdn.net/abcdef314159
原始碼:\sources\Android-25
PriorityQueue通過名字也可以看的出來,是優先佇列,PriorityBlockingQueue是優先阻塞佇列,這兩個類其實方法都差不多,只不過PriorityBlockingQueue操作的時候會加鎖ReentrantLock,PriorityQueue操作的時候是沒有加鎖的,程式碼也不多,簡單看一下,主要以PriorityQueue中的方法為主,會有部分PriorityBlockingQueue類的方法先看一個構造方法
構造方法比較多,這裡只;列出了其中的一個,這個沒啥可說的,下面再看初始化集合的方法initElementsFromCollection/** * Creates a {@code PriorityQueue} with the specified initial capacity * that orders its elements according to the specified comparator. * * @param initialCapacity the initial capacity for this priority queue * @param comparator the comparator that will be used to order this * priority queue. If {@code null}, the {@linkplain Comparable * natural ordering} of the elements will be used. * @throws IllegalArgumentException if {@code initialCapacity} is * less than 1 */ public PriorityQueue(int initialCapacity, Comparator<? super E> comparator) { // Note: This restriction of at least one is not actually needed, // but continues for 1.5 compatibility if (initialCapacity < 1) throw new IllegalArgumentException(); this.queue = new Object[initialCapacity];//初始化空間 //比較器,可以為空,如果為空,queue中的元素要實現Comparable介面 this.comparator = comparator; }
這個方法是私有的,下面來看一個呼叫它的方法initFromCollection// 從集合c中初始化元素 private void initElementsFromCollection(Collection<? extends E> c) { Object[] a = c.toArray(); // If c.toArray incorrectly doesn't return Object[], copy it. //copy集合c到陣列a中 if (a.getClass() != Object[].class) a = Arrays.copyOf(a, a.length, Object[].class); int len = a.length; if (len == 1 || this.comparator != null) for (Object e : a) if (e == null)//不允許為null throw new NullPointerException(); this.queue = a;//copy的元素 this.size = a.length;//陣列的大小 }
/**
* Initializes queue array with elements from the given Collection.
*
* @param c the collection
*/
private void initFromCollection(Collection<? extends E> c) {
initElementsFromCollection(c);
//初始化完成之後,要重新建堆
heapify();
} /**
* Establishes the heap invariant (described above) in the entire tree,
* assuming nothing about the order of the elements prior to the call.
*/
@SuppressWarnings("unchecked")
private void heapify() {
//從插入元素的最後一個節點的父節點位置開始調整,這裡可能不太好理解的是i和size之間的關係,
//正常情況下父與子的關係left(i)=2i+1,right(i)=2i+2;(這裡的i是陣列下標),這裡的size是陣列的
//長度,這裡從i開始調整有個好處,就是下面的每次調整都會讓父節點成為最小的,所以到後面的時候不需要
//每次都迴圈到葉子節點,大大減少了迴圈的次數,如果從0開始,就不會有這樣的好處了
for (int i = (size >>> 1) - 1; i >= 0; i--)
siftDown(i, (E) queue[i]);
} /**
* Increases the capacity of the array.
*
* @param minCapacity the desired minimum capacity
*/
//增加空間
private void grow(int minCapacity) {
int oldCapacity = queue.length;
// Double size if small; else grow by 50%
//如果原來空間小於64,則增加2,否則擴大一倍
int newCapacity = oldCapacity + ((oldCapacity < 64) ?
(oldCapacity + 2) :
(oldCapacity >> 1));
// overflow-conscious code
if (newCapacity - MAX_ARRAY_SIZE > 0)// 如果太大,則要重新調整
newCapacity = hugeCapacity(minCapacity);
queue = Arrays.copyOf(queue, newCapacity);
}grow是根據傳進來的最小空間來初始化陣列大小,其中hugeCapacity表示如果初始化空間太大,則需要重新調整size的大小。繼續看下面的方法,add,其實他呼叫的是offer方法,下面看一下offer方法
/**
* Inserts the specified element into this priority queue.
*
* @return {@code true} (as specified by {@link Queue#offer})
* @throws ClassCastException if the specified element cannot be
* compared with elements currently in this priority queue
* according to the priority queue's ordering
* @throws NullPointerException if the specified element is null
*/
public boolean offer(E e) {//插入元素
if (e == null)
throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length)//如果空間太小
grow(i + 1);//增加空間
size = i + 1;//size加1
if (i == 0)
queue[0] = e;//如果原來沒有元素,則直接新增
else
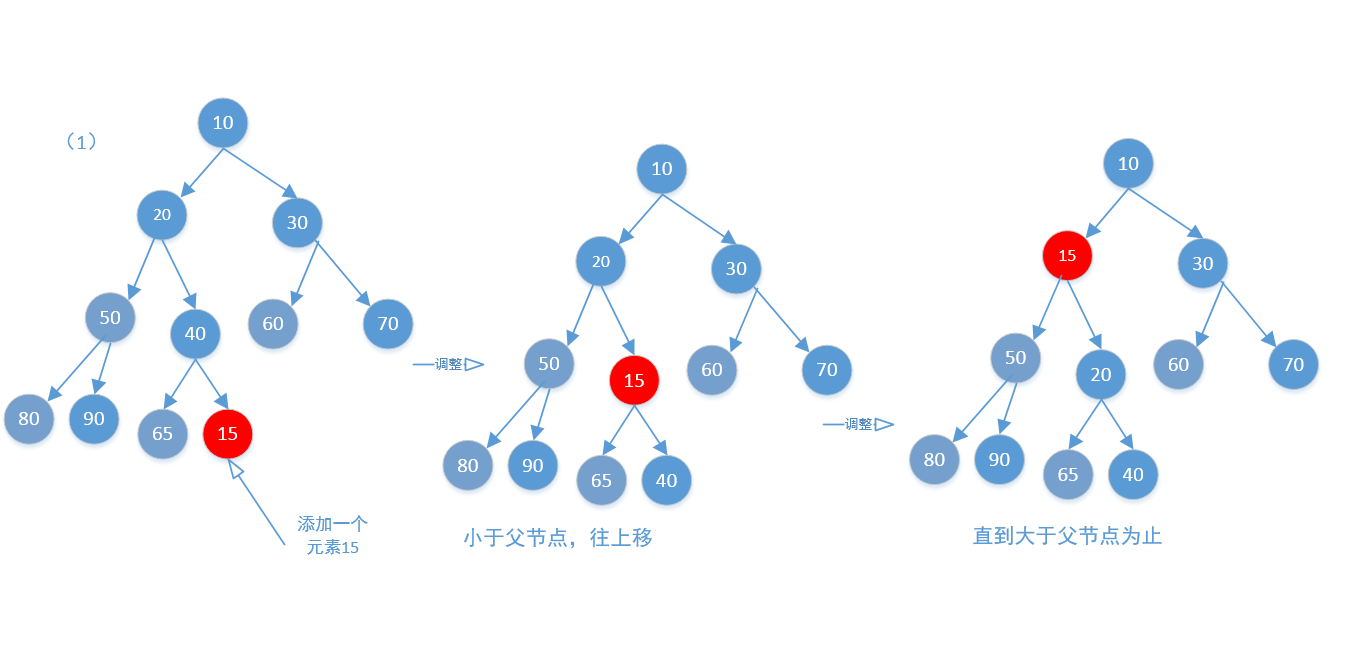
//新增,向上調整,新增的雖然是在陣列中,但是可以把它想象成為一顆二叉樹,
//新增的時候是新增到陣列的最後,相當於二叉樹的葉子節點,因為是需要調整的,所以需要往上調整,
//這個待會可以看一下下面的siftUp方法
siftUp(i, e);
return true;
} /**
* Inserts item x at position k, maintaining heap invariant by
* promoting x up the tree until it is greater than or equal to
* its parent, or is the root.
*
* To simplify and speed up coercions and comparisons. the
* Comparable and Comparator versions are separated into different
* methods that are otherwise identical. (Similarly for siftDown.)
*
* @param k the position to fill
* @param x the item to insert
*/
private void siftUp(int k, E x) {//根據是否有比較器,旋轉哪種調整方式
if (comparator != null)
siftUpUsingComparator(k, x);
else
siftUpComparable(k, x);
} @SuppressWarnings("unchecked")
private void siftUpUsingComparator(int k, E x) {
//(1)往上調整,注意這裡的x不一定是下標為k的元素,如果不明白,可以看一下下面的removeAt方法接知道。
while (k > 0) {
int parent = (k - 1) >>> 1;//k位置的父節點的下標
Object e = queue[parent];// 父元素
//如果當前的比父的大就不需要調整了,直接退出迴圈,因為父節點是小於子節點的
if (comparator.compare(x, (E) e) >= 0)
break;
//父子交換
queue[k] = e;
k = parent;
}
queue[k] = x;// 把x放入高指定位置
} @SuppressWarnings("unchecked")
private void siftDownUsingComparator(int k, E x) {
int half = size >>> 1;
//(2)這裡為什麼沒有等於,因為size不是下標,是陣列的長度,half所在的元素其實就是葉子節點,
//只有k所在元素有子節點的時候才會調整,如果沒有子節點就沒法往下調整,所以如果等於沒有意義,
while (k < half) {
int child = (k << 1) + 1;//預設是左子節點
Object c = queue[child];//預設是左子節點
int right = child + 1;//右子節點
//比較左右兩個節點,把小的儲存到c中
if (right < size &&
comparator.compare((E) c, (E) queue[right]) > 0)
c = queue[child = right];
//如果x比連個子節點都小,就沒有必要往下調整了,直接返回
if (comparator.compare(x, (E) c) <= 0)
break;
//把最小的儲存到k,然後迴圈
queue[k] = c;
k = child;
}
queue[k] = x;//把x插入到查詢的k位置。
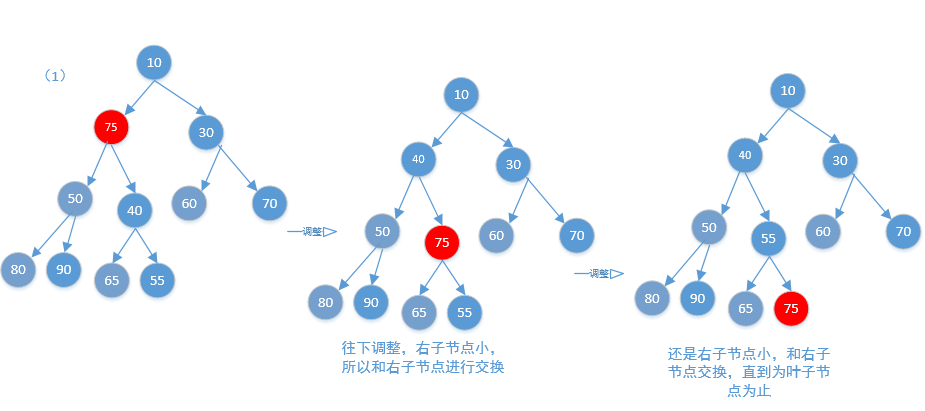
}新增的時候是從最後一個新增的,也就是葉子節點,但往上調整並不是每次都是從最後的葉子節點開始的,還有移除等方法都有可能呼叫這個方法,其實原理都一樣,把當前需要調整的節點和父節點對比,如果小於父節點就交換,如果大於停止迴圈,不要交換,OK,下面再來看一下往下調整的方法圖
OK,下面再看另一個方法poll(),表示獲取二叉樹的根元素
//獲取第一個元素,也就是二叉樹的根
@SuppressWarnings("unchecked")
public E poll() {
if (size == 0)
return null;
int s = --size;// size減1
modCount++;
E result = (E) queue[0];//移除的元素,
E x = (E) queue[s];//最右一個元素
queue[s] = null;//讓最後一個為空
if (s != 0)
siftDown(0, x);//往下調整
return result;
} /**
* Removes the ith element from queue.
*
* Normally this method leaves the elements at up to i-1,
* inclusive, untouched. Under these circumstances, it returns
* null. Occasionally, in order to maintain the heap invariant,
* it must swap a later element of the list with one earlier than
* i. Under these circumstances, this method returns the element
* that was previously at the end of the list and is now at some
* position before i. This fact is used by iterator.remove so as to
* avoid missing traversing elements.
*/
// 移除下標為i的元素
@SuppressWarnings("unchecked")
E removeAt(int i) {
// assert i >= 0 && i < size;
modCount++;
int s = --size;
if (s == i) // removed last element
queue[i] = null;//如果是最後一個直接刪除,不需要在調整,因為最後一個在二叉樹中是葉子節點
else {
E moved = (E) queue[s];//記錄最後一個元素
queue[s] = null;//然後把最後一個元素的位置置null
//從i位置開始往下調整,相當於把最後的moved放到i位置上然後調整,
siftDown(i, moved);
if (queue[i] == moved) {
//如果往下調整的時候下面的兩個子節點都比他大,是調整不了的,所以需要在往上調整,
siftUp(i, moved);
if (queue[i] != moved)
return moved;
}
}
return null;
}OK,到目前為止,基本上分析完畢。