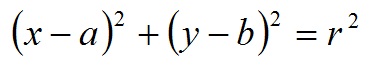霍夫圓變換

基本原理 

關於基本原理，其思想大概跟霍夫線變換相似，但是有兩種說法。

第一種：

在霍夫線變換中，笛卡爾X-Y直角座標系中的直線，變換到霍夫空間中則為1個點

因此類比可得，笛卡爾X-Y直角座標系中的圓，變換到abr空間中，則為一條曲線，具體如下：

X-Y直角座標系下圓方程：

對應的引數方程為：

所以在abr組成的三維座標系中，一個點可以唯一確定一個圓。

那麼，當我們固定（x,y），選取（a,b,r） 的不同組合，可以得到xy直角座標系中經過某點(X,Y)的所有圓對應，

而在笛卡爾的xy座標系中經過某一點的所有圓對映到abr座標系中就是一條三維的曲線。【這句話應該是不嚴謹的，正確的說法看後面的第二種敘述】

個人認為，上面的話，應該是對於某點（x,y），

固定X時，選取不同(a,r)組合，可以得到一條(a,r)座標系下的曲線

固定Y時，選取不同(b,r)組合，可以得到一條(b,r)座標系下的曲線 

 這裡，我們先繼續認為上面的敘述沒有問題，即經過點(X,Y)的所有圓變換到（a,b,r）空間下是一條空間曲線。那麼這條曲線上的一點，則對應一個圓。

這時候，看（a,b,r）座標系，若該座標系中有某點(a,b,r）固定，那麼經過該點的空間曲線越多，說明對應笛卡爾X-Y直角座標系中共圓的點越多。當設定一個閾值，則可判斷X-Y座標系中是否有圓了。

 第二種：

X-Y直角座標系下圓方程：

現假設（x,y）是引數，即（x,y）固定，假設為（1，1）

那麼以（a,b,r）為變數的方程，對應的空間圖形是一個這樣一個曲面，貌似是圓錐？

matlab畫圖程式碼：

>> a=-8:0.5:8;
>> b=a;
>> [A,B]=meshgrid(a,b);
>> R=sqrt((1-A).^2+(1-B).^2);
>> mesh(A,B,R);

這就跟上面第一種說法的敘述有矛盾了，這裡表明在笛卡爾的xy座標系中經過某一點的所有圓對映到abr座標系中是一個圓錐體。

那麼，在這個曲面上的每一個點，則對應 X-Y座標系下的一個經過點（x，y）的圓。

也就是說，在（a，b，r）座標系中，假設有固定的某點(a0,b0,r0），若經過該點的曲面越多，則表示對應X-Y直角座標系中有多個點共這個圓。

原理部分就先到這裡，希望有大神指出紕漏。 

參考文章：