神經網路學習1
神經網路模型建立在很多神經元之上,每個神經元又是一個學習模型。這些蛇恩靜元也叫作啟用單元。下面我們以一個邏輯斯特迴歸模型作為自身學習模型,引數又可以被稱為權重。

其中x1,x2,x3是輸入單元,我們將原始資料輸入給它們。a1,a2,a3是中間單元,它們負責將資料進行處理,然後呈遞到下一層。最後是輸出單元,它負責計算hθ(x)。如上圖所示,第一層為輸入錯,最後一次為輸出層,中間一層為隱藏層。我們的每一層其實都有一個偏差單位,相當於x0,其值始終為1。
 代表第j層的第i個啟用單元。θ(i)權重矩陣它控制從某一層到某一層的對映。θ(i)的維度是3*4。
代表第j層的第i個啟用單元。θ(i)權重矩陣它控制從某一層到某一層的對映。θ(i)的維度是3*4。
對於上圖所示的模型,啟用單元和輸出分別表達為:
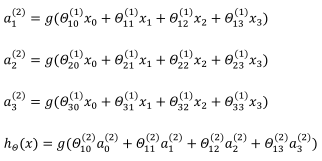
在這裡a(1)=x=  z(2)=
z(2)=

加上偏置單元x0=1對a(2)並無影響。
接下來我們擬合神經網路的代價引數
假設我們要區分出K個類,那麼K個類有K個輸出單元(K>-3)
(hθ(x))i=第i個輸出
那麼我們的代價函式就為
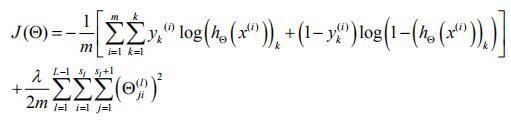
我們現在設δ為誤差,δ上面的引數為(l)下面的引數是j,表示第l層的第j個輸出項和y之間的誤差。
假如我們現在又一個4層的訓練集,按照向前傳播演算法可以得到下圖所示算式。
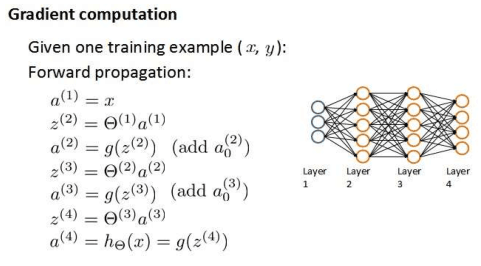
我們現在使用向後傳播演算法來計算誤差δ。
則δ(4)=a(4)-y
我們利用這個誤差來計算前一層的誤差:
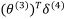 則是權重導致的誤差的和。然後可以依次類推之後的誤差。而第一層是輸入變數,不存在誤差。
則是權重導致的誤差的和。然後可以依次類推之後的誤差。而第一層是輸入變數,不存在誤差。
當我們有了所有的表示式後,就可以計算代價函式的偏導數了,假設λ=0,即我們不做任何正則化處理時有:
在上面這個式子裡,它的下標分別代表著下面這幾種意思:
l代表目前所計算的是第幾層。
j代表目前計算層
中的啟用單元的下標,也將是下一層的第j個輸入變數的下標。
i代表下一層中誤差單元的下標,是受到權重矩陣中第i行影響的下一層中的誤差單元的下標。
如果我們考慮正則化處理,並且我們的訓練集是一個矩陣而不是向量,在上面的特殊情況中,我們需要計算每一層的誤差單元來計算代價函式的偏導數。在更為一般的情況中,我們同樣需要計算每一層的誤差單元,但是我們需要為整個訓練集計算誤差單元,此時的誤差單元也是一個矩陣,我們用大寫的δ來表示這個誤差矩陣。我們計算大寫δ的演算法表示為:

即首先用整向傳播方法計算出每一層的啟用單元,利用訓練集的結果與神經網路預測的結果求出最後一層的誤差,然後利用該誤差運用反向傳播法求取直至第二層的所有誤差。
那麼我們一般情況下的偏導數的計算方法如下:

