【學習筆記1】吳恩達_卷積神經網路_第一週卷積神經網路(1)
一、卷積神經網路
1.邊緣檢測
不同的語言中表示卷積的函式不同,在Python中為在tensorflow裡為
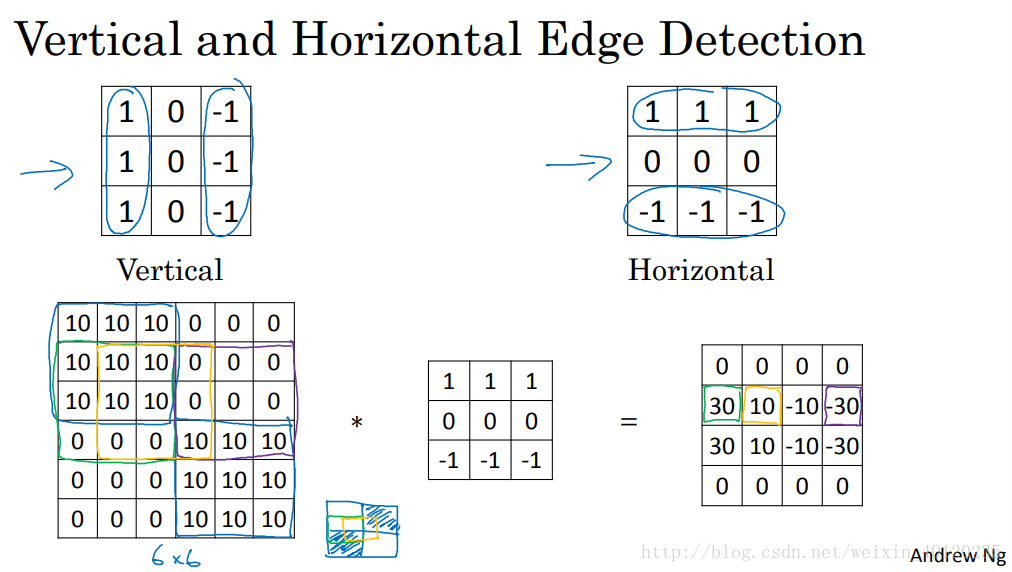
濾波器:垂直、水平邊緣檢測。
Sobel filter:其優點在於增加了中間一行元素的權重,即影象中間的畫素點提高,會使結果的魯棒(robust)性提高。
Scharr filter
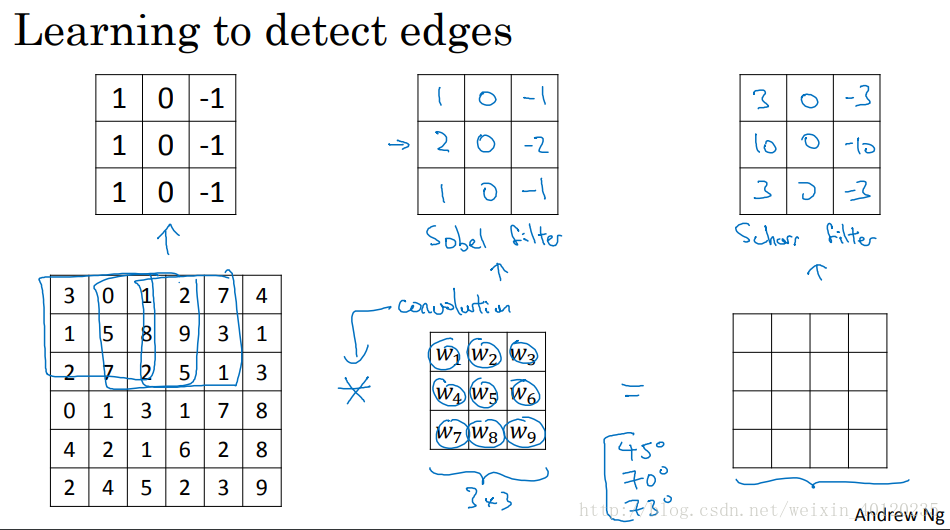
通過反向傳播方法得到九個數的濾波器,得到任意角度的邊緣檢測。將這九個數設為引數,讓神經網路去學習它,得到較為低階的特徵,如邊緣特徵
2.Padding
圖片的大小為n*n,卷積大小為f*f,輸出圖片維度為(n-f+1)*(n-f+1),這樣做的缺點:a.會使圖片縮小;b.角落邊的畫素只被一個輸出所碰觸,意味著丟失很多邊緣資訊。為了解決這兩個問題,需要在影象輸入時,在影象四周做一圈填充(Padding),通常使用0作填充。將p=padding number=1,則影象變為(n+2p)*(n+2p),輸出影象最終為(n+2p-f+1)*(n+2p-f+1),若f=3,p=1則輸出影象畫素等於原來影象畫素即為Same convolution,同時削弱了缺點b的影響。
填充層數的不同,產生不同的卷積:
*當f=5時,p=2,輸出與輸入影象大小相同。
在卷積神經網路中f很少為偶數,當f為偶數時可能需要引入不對稱填充,同時,如果f為奇數,會產生中心畫素點,便於指出卷積所在位置。
3.卷積步長(stride)
改變步長,輸出影象維度改變。
根據上圖公式,若結果不是一個整數,向下取整數,這種方法要求卷積掃過的面積不包含填充層。
關於互相關和卷積的技術性建議:
在數學和技術中對於卷積的定義不同。在數學中,卷積是做元素乘積求和之前,將卷積進行沿豎直和水平軸的翻轉;在深度學習的操作裡我們進行的操作實際為互相關,不進行翻轉操作,稱作卷積操作。