Abstract

• 本論文提出一種新的全卷積孿生網路作為基本的跟蹤演算法，這個網路在ILSVRC15的目標跟蹤視訊資料集上進行端到端的訓練。我們的跟蹤器在幀率上超過了實時性要求，儘管它非常簡單，但在多個benchmark上達到最優的效能。

1. Introduction

• 最近很多研究通過使用預訓練模型來解決上述問題。這些方法中，要麼使用網路內部某一層作為特徵的shallow方法（如相關濾波）；要麼是使用SGD方法來對多層網路進行微調。然而shallow的方法沒有充分利用端到端學習的益處，而使用SGD微調雖然能到達時最優結果，但卻難以達到實時性的要求。
• 我們提出另一種替代性的方法。這個方法在初始離線階段把深度卷積網路看成一個更通用的相似性學習問題，然後在跟蹤時對這個問題進行線上的簡單估計。這篇論文的關鍵貢獻就在於證明這個方法在benchmark上可以達到非常有競爭性的效能，並且執行時的幀率遠超實時性的要求。具體點講，我們訓練了一個孿生網路在一個較大的搜尋區域搜尋樣本圖片。本文另一個貢獻在於，新的孿生網路結構是一個關於搜尋區域的全卷積網路：密集高效的滑動視窗估計可通過計算兩個輸入的互相關性並插值得到。

2. Deep similarity learning for tracking

• 跟蹤任意目標的學習可看成是相似性問題的學習。我們提出學習一個函式 $f$
  ( x , z ) f(x,z) 來比較樣本影象 $z$
  z 和具有相同大小的搜尋影象 $x$ 的相似性。如果兩個影象描述的是同一個目標，則返回高分，否則返回低分。
• 我們用深度神經網路來模擬函式 $f$，而深度卷積網路中相似性學習最典型的就是孿生結構。孿生網路對兩個輸入 $z$ 和 $x$ 進行相同的變換 $\varphi$ ，然後將得到的輸出送入函式 $g$，最後得到相似性度量函式為： $f(z,x)=g(\varphi(z),\varphi(x)) \tag{1}$ 1.函式 $g$ 是一個簡單的距離或相似性度量
  2. $\varphi$ 相當於特徵提取器

2.1 Fully-convolutional Siamese architecture

• 網路結構如下圖所示
  1. $z$ 表示樣本影象（即目標）
  2. $x$ 表示待搜尋影象
  
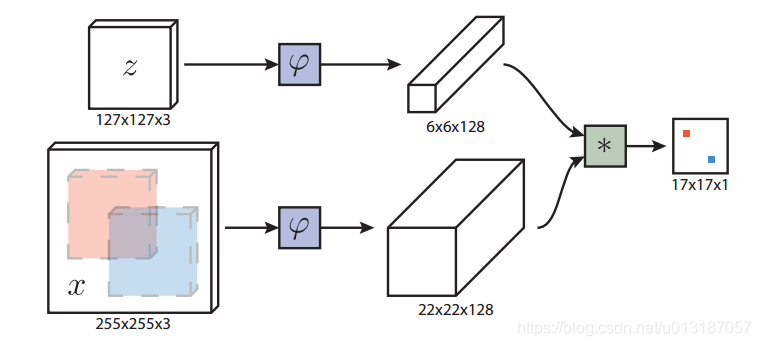
• 全卷積網路的優點是待搜尋影象不需要與樣本影象具有相同尺寸，可以為網路提供更大的搜尋影象作為輸入，然後在密集網格上計算所有平移視窗的相似度。本文的相似度函式使用互相關，公式如下 $f(z,x)=\varphi(z) * \varphi(x) + b\mathcal 1 \tag{2}$ 1. $b\mathcal 1$ 表示在得分圖中每個位置的取值
  2.上式可將 $\varphi(z)$ 看成卷積核，在 $\varphi(x)$ 上進行卷積
• 跟蹤時以上一幀目標位置為中心的搜尋影象來計算響應得分圖，將得分最大的位置乘以步長即可得到當前目標的位置。

2.2 Training with large search images

• 我們用判別方法來對正、負樣本對進行訓練，其邏輯損失定義如下： $\mathcal l(y,v)=log(1+exp(-yv))\tag{3}$ 1. $y\in(+1,-1)$ 表示真值
  2. $v$ 表示樣本–搜尋影象的實際得分
  3.上式表示的正樣本的概率為 $\frac{1}{1+e^{-v}}$，負樣本的概率為 $1-\frac{1}{1+e^{-v}}$，則按交叉熵的公式很容易得到式 $(3)$ 的loss
• 訓練時採用所有候選位置的平均loss來表示，公式如下： $L(y,v)=\frac{1}{\mathcal D}\sum_{u\in \mathcal D}\mathcal l(y[u],v[u])\tag{4}$ 1. $\mathcal D$ 表示最後得到的 score map
  2. $u$ 表示 score map 中的所有位置
• 訓練的卷積引數 $\theta$ 通過SGD來最小化如下問題得到： $arg\ \underset {\theta}{min}=\underset {(z,x,y)}{E}\ L(y,f(z,x;\theta))\tag{5}$
• 訓練樣本對 $(z,x)$ 從標註的視訊資料集得到，如下圖所示
  1.搜尋區域 $x$ 以目標區域 $z$ 為中心
  2.如果超出影象則用畫素平均值填充，保持目標寬高比不變
  3.訓練時不考慮目標類別
  4.網路的輸入尺寸統一
  
• 網路輸出正負樣本的確定：在輸入搜尋影象上（如 $255*255$），只要和目標的距離不超過R，那就算正樣本，否則就是負樣本，用公式表示如下： $y[u]=\left\{\begin{matrix} & +1\quad if\ k||u-c||\leq R\\ &-1\qquad otherwise\quad . \end{matrix}\right.\tag{6}$ 1. $k$ 為網路的總步長
  2. $c$ 為目標的中心
  3. $u$ 為score map的所有位置
  4. $R$ 為定義的半徑

2.3 Practical considerations

• Dataset curation
  1.樣本影象大小 $127\times 127$，搜尋影象大小 $255\times255$
  2.影象的縮放與填充如式所示： $s(w+2p)\times s(h+2p)=A$
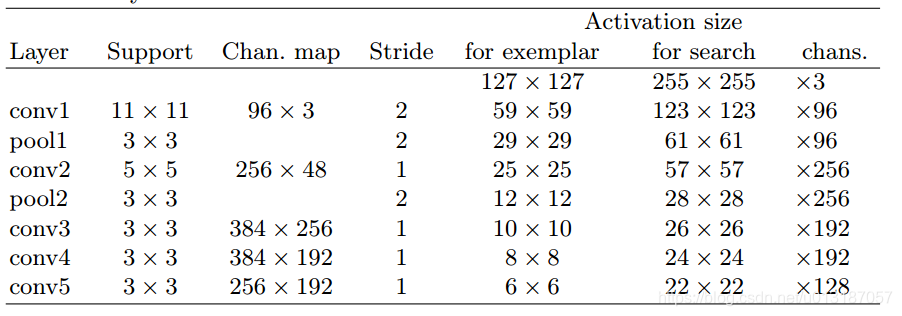
  3.從ILSVRC15的4500個視訊中選出4417個視訊，超過2,000,000個標註的跟蹤框作為訓練集
• Network architecture
  1.前兩個卷積層後有池化層；
  2.每個卷積層後都有ReLU層（conv5除外）；
  3.每個線性層後都加上BN；
  4.卷積層沒有加padding；
  

3. Experiments

3.1 Implementation details

• Training
  1.梯度下降採用SGD
  2.用高斯分佈初始化引數
  3.訓練50個epoch，每個epoch有50,000個樣本對
  4.mini-batch等於8
  5.學習率從 $10^{-2}$ 衰減到 $10^{-8}$