Bash and a Tough Math Puzzle(CodeForces-11D)(線段樹)
文章目錄
題目
傳送門
題目
Bash likes playing with arrays. He has an array , , … an of n integers. He likes to guess the greatest common divisor (gcd) of different segments of the array. Of course, sometimes the guess is not correct. However, Bash will be satisfied if his guess is almost correct.
Suppose he guesses that the gcd of the elements in the range of a is x. He considers the guess to be almost correct if he can change at most one element in the segment such that the gcd of the segment is x after making the change. Note that when he guesses, he doesn’t actually change the array — he just wonders if the gcd of the segment can be made x. Apart from this, he also sometimes makes changes to the array itself.
Since he can’t figure it out himself, Bash wants you to tell him which of his guesses are almost correct. Formally, you have to process q queries of one of the following forms:
— Bash guesses that the gcd of the range is x. Report if this guess is almost correct. — Bash sets ai to y. Note: The array is 1-indexed.
Input The first line contains an integer n — the size of the array.
The second line contains n integers — the elements of the array.
The third line contains an integer q — the number of queries.
The next q lines describe the queries and may have one of the following forms:
Guaranteed, that there is at least one query of first type.
Output For each query of first type, output “YES” (without quotes) if Bash’s guess is almost correct and “NO” (without quotes) otherwise.
Examples Input
3
2 6 3
4
1 1 2 2
1 1 3 3
2 1 9
1 1 3 2
Output
YES
YES
NO
Input
5
1 2 3 4 5
6
1 1 4 2
2 3 6
1 1 4 2
1 1 5 2
2 5 10
1 1 5 2
Output
NO
YES
NO
YES
Note In the first sample, the array initially is {2, 6, 3}.
For query 1, the first two numbers already have their gcd as 2.
For query 2, we can achieve a gcd of 3 by changing the first element of the array to 3. Note that the changes made during queries of type 1 are temporary and do not get reflected in the array.
After query 3, the array is now {9, 6, 3}.
For query 4, no matter which element you change, you cannot get the gcd of the range to be 2.
題目大意
現在給你一個長度為的序列接下來有q次操作分為兩種: 1 l r x:查詢區間是否能通過不改變或只臨時改變其中一個元素的值使得 輸出"YES"或“NO” 2 i y:將a[i]值改為y
思路
這是一道很裸的線段樹的題.我們對於一個區間[L,R]只需要記錄一下該區間所有元素的最大公因數為多少
我們令Gcd[l,r]為該區間所有元素最大公因數,顯然有:
那麼對於操作2,我們直接下傳值返回更新
對於操作1,我們知道如果Gcd[L,R]為x的倍數的話,我們可以直接令其中任意一個數為x就可以滿足條件
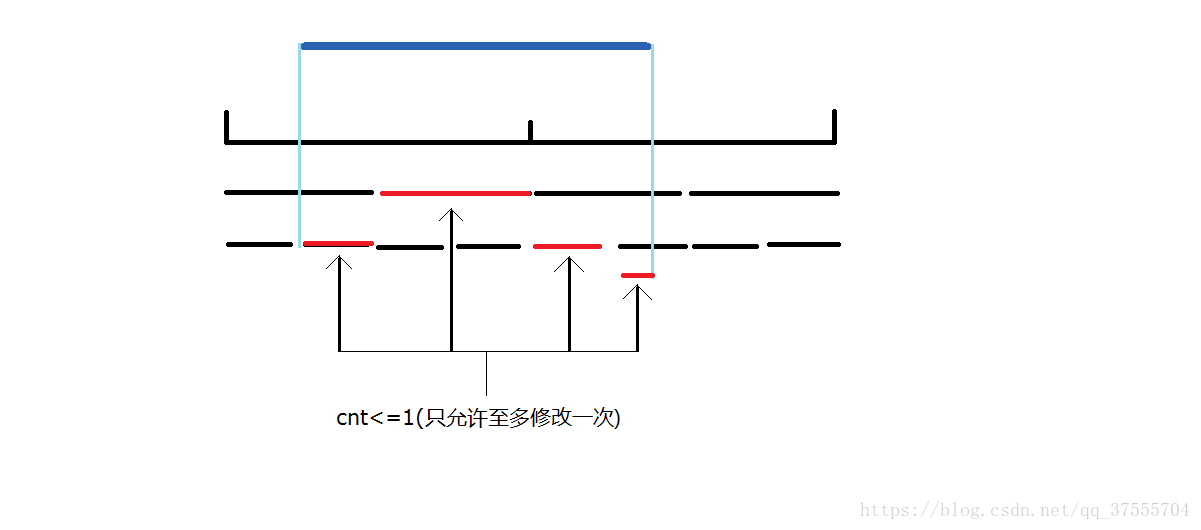
我們令cnt篩除不符合條件的元素的變數
如果不滿足,由於最多隻可修改一次,那麼我們把查詢區間分成若干個子區間,如果有區間Gcd[l,r]%x!=0那麼我們只允許出現一個元素不符合條件
如果該區間的左右子區間(有點繞)Gcd均不符,那麼不符合的元素肯定大於1個,就直接返回,而如果到了葉節點,就直接cnt++,而如果只有一個兒子Gcd不符,遞迴處理即可
程式碼
常規版
//343ms 23500kB
#include<set>
#include<map>
#include<ctime>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<climits>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
int read(){
int f=1,x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
return x*f;
}
#define lch i<<1
#define rch i<<1|1
#define MAXN 500000
#define INF 0x3f3f3f3f
#define Mod int(1e9+7)
struct Tree{
int l,r,gcd;
Tree(){}
Tree(int L,int R,int G){l=L,r=R,gcd=G;}
}tree[MAXN<<2];
inline int gcd(int a,int b){return !b?a:gcd(b,a%b);}
void Build(int i,int l,int r){
tree[i].l=l,tree[i].r=r;
if(l==r){
tree[i].gcd=read();
return ;
}
int mid=(l+r)>>1;
Build(lch,l,mid);
Build(rch,mid+1,r);
tree[i].gcd=gcd(tree[lch].gcd,tree[rch].gcd);
return ;
}
void Update(int i,int p,int x){
if(tree[i].l==p&&tree[i].r==p){
tree[i].gcd=x;
return ;
}
int mid=(tree[i].l+tree[i].r)>>1;
if(p<=mid) Update(lch,p,x);
else Update(rch,p,x);
tree[i].gcd=gcd(tree[lch].gcd,tree[rch].gcd);
return ;
}
int cnt;
void Query(int i,int L,int R,int x){
if(cnt>1) return ;
if(L<=tree[i].l&&tree[i].r<=R){
if(tree[i].gcd%x==0)
return ;
else if(tree[i].l==tree[i].r){
cnt++;
return ;
}
int lg=tree[lch].gcd,rg=tree[rch].gcd;
if(lg%x&&rg%x){
cnt=2;
return ;
}
if(lg%x)
Query(lch,L,R,x);
if(rg%x)
Query(rch,L,R,x);
return ;
}
int mid=(tree[i].l+tree[i].r)>>1;
if(L<=mid) Query(lch,L,R,x);
if(mid+1<=R) Query(rch,L,R,x);
return ;
}
int main(){
int n=read();
Build(1,1,n);
int q=read();
for(int i=1;i<=q;i++){
int o=read(),l,r,p,x;
if(o-1) p=read(),x=read(),Update(1,p,x);
else l=read(),r=read(),x=read(),cnt=0,Query(1,l,r,x),puts(cnt>1?"NO":"YES");
}
return 0;
}
懶人加速版
//296 ms7800 KB
#include<set>
#include<map>
#include<ctime>
#include<queue>
#include<cmath>
#include<cstdio>
#include<vector>
#include<climits>
#include<cstring>
#include<iostream>
#include<algorithm>
#define LL long long
using namespace std;
int read(){
int f=1,x=0;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
return x*f;
}
#define lch i<<1
#define rch i<<1|1
#define MAXN 500000
#define INF 0x3f3f3f3f
#define Mod int(1e9+7)
int Gcd[MAXN<<2];
inline int gcd(int a,int b){return !b?a:gcd(b,a%b);}
void Build(int i,int l,int r){
if(l==r){
Gcd[i]=read();
return ;
}
int mid=(l+r)>>1;
Build(lch,l,mid);
Build(rch,mid+1,r);
Gcd[i]=gcd(Gcd[lch],Gcd[rch]);//向上更新
return ;
}
void Update(int i,int l,int r,int p,int x){
if(l==p&&r==p){
Gcd[i]=x;
return ;
}
int mid=(l+r)>>1;
if(p<=mid) Update(lch,l,mid,p,x);
else Update(rch,mid+1,r,p,x);
Gcd[i]=gcd(Gcd[lch],Gcd[rch]);
return ;
}
int cnt;
void Query(int i,int l,int r,int L,int R,int x){
if(cnt>1) return ;//不符合直接返回
int mid=(l+r)>>1;
if(L<=l&&r<=R){//該區間為查詢區間子區間
if(Gcd[i]%x==0)//子區間符合條件
return ;
else if(l==r){//為葉節點
cnt++;
return ;
}//子區間Gcd%x!=0,cnt必定會改變
int lg