空間變換網路Spatial Transformer Networks(STN)
相關理論
（見https://zhuanlan.zhihu.com/p/37110107）
在理解STN之前，先簡單瞭解一下基本的仿射變換、雙線性插值。
1.仿射變換（Affine transformation）
下面的所有變換假設都是針對一幅影象，即一個三維陣列（HWC），這裡為簡單起見，假設影象都是單通道（C=1）的。首先說明一下待會要用到的符號：
(x,y): 原影象中某一點A的位置
(x′,y′): 變換後圖像中A點對應的位置
平移（translation）
若將原影象沿x和y方向分別平移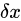 
和
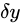，即：
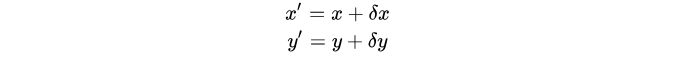
寫成矩陣形式如下：
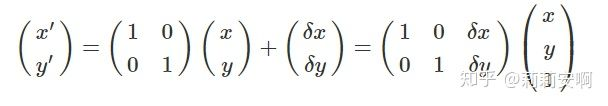
縮放（Scaling）
假設將影象分別沿x和y方向分別縮放p倍和q倍，且p>0，q>0，即：
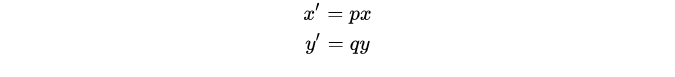
寫成矩陣形式如下：
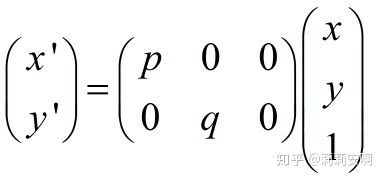
旋轉（Rotation）
圖2.旋轉變換示意圖
寫成矩陣形式如下：
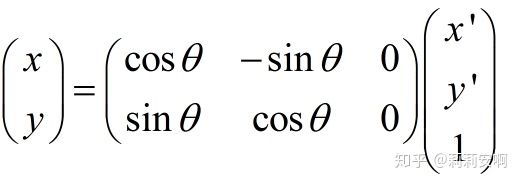
剪下(Shear)
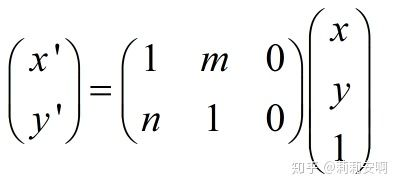
剪下變換指的是類似於四邊形不穩定性那種性質，方形變平行四邊形。任意一邊都可以被拉長，以一定比例的x補償y，也以一定比例的y補償x。
仿射變換（Affine transformation）
其實上面幾種常見變換都可以用同一種變換來表示，就是仿射變換，它有更一般的形式，如下：
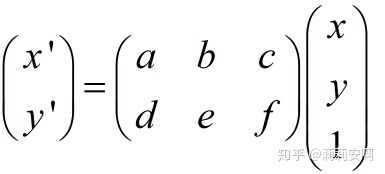
a,b,c,d,e,f取不同的值就可以表示上述不同的變換。當6個引數取其上述變換以外的值時，為一般的仿射變換，效果相當於從不同的位置看同一個目標。
2.雙線性插值（詳見https://blog.csdn.net/qq_30339595/article/details/84945474）
STN演算法細節
（見https://zhuanlan.zhihu.com/p/42692080）
-
ST
ST由三個模組組成： -
Localisation Network：該模組學習仿射變換矩陣（附件A）；
-
Parameterised Sampling Grid：根據Localisation Network得到仿射變換矩陣，得到輸出Feature Map和輸入Feature Map之間的位置對映關係；
-
Differentiable Image Sampling：計算輸出Feature Map的每個畫素點的值。
STM的結構見圖1：
圖1：STM的框架圖
ST使用的插值方法屬於“後向插值”的一種，即給定輸出Feature Map上的一個點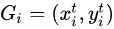
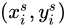，如果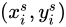 
為整數，則輸出Feature Map在 
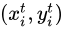處的值和輸入Feature Map在 
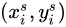處的值相同，否則需要通過插值的方法得到輸出Feature Map在
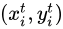處的值。
說了後向插值，當然還有一種插值方式叫做前向插值，例如在Mask R-CNN中介紹的插值方法。
Localisation Network
Localisation Network是一個小型的卷積網路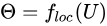 
，其輸入是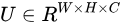
，輸出是仿射矩陣 
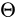的六個值。因此輸出層是一個有六個節點回歸器。
![\ theta = \left[ \begin{matrix} \theta_{11} & \theta_{12} & \theta_{13} \ \theta_{21} & \theta_{22} & \theta_{23} \end{matrix} \tag{1} \right]](https://img-blog.csdnimg.cn/20181210201931780.png)
下面的是原始碼中給出的Localisation Network的結構:
locnet = Sequential()
locnet.add(MaxPooling2D(pool_size=(2,2), input_shape=input_shape))
locnet.add(Conv2D(20, (5, 5)))
locnet.add(MaxPooling2D(pool_size=(2,2)))
locnet.add(Conv2D(20, (5, 5)))
locnet.add(Flatten())
locnet.add(Dense(50))
locnet.add(Activation('relu'))
locnet.add(Dense(6, weights=weights))
Parameterised Sampling Grid
Parameterised Sampling Grid利用Localisation Network產生的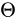 
進行仿射變換，即由輸出Feature Map上的某一位置 
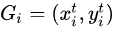根據變換引數 
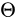得到輸入Feature Map的某一位置 
：
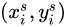![\left(\begin{matrix}x_i^s \y_i^s\end{matrix} \right) = \mathcal{T}_\theta(G_i) = \Theta\left(\begin{matrix}x_it\y_it\1\end{matrix}\right) = \left[\begin{matrix}\theta_{11} & \theta_{12} & \theta_{13} \ \theta_{21} & \theta_{22} & \theta_{23}\end{matrix}\right] \left(\begin{matrix}x_it\y_it\1\end{matrix}\right) \tag{2}](https://img-blog.csdnimg.cn/20181210202042505.png)
裡需要注意兩點：
-
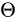可以是一個更通用的矩陣，並不侷限於仿射變換，甚至不侷限於6個值； -
對映得到的
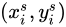一般不是整數，因此不能 
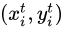不能使用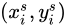 
的值，而是根據它進行插值，也就是我們下一節要講的東西。
Differentiable Image Sampling
如果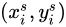 
為一整數，那麼輸出Feature Map的 
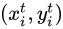處的值便可以從輸入Feature Map上直接對映過去。然而在的1.2節我們講到， 
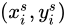往往不是整數，這時我們需要進行插值才能確定輸出其值，在這個過程叫做一次插值，或者一次取樣（Sampling）。插值過程可以用下式表示：
![V_{i}^c = \sum^H_n \sum^W_m U^c_{nm} k(x_i^s-m;\Phi_x) k(y_i^s -m; \Phi_y) ,\quad where\quad \forall i\in[1,...,H'W'],\forall c\in[1,...,C] \tag{3}](https://img-blog.csdnimg.cn/20181210202324452.png)
在
上式中，函式 f() 表示插值函式，本文將以雙線性插值為例進行解析，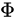 
為 f() 中的引數， 
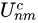為輸入Feature Map上點 (n, m, c) 處的值， 
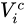便是插值後輸出Feature Map的 
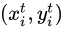處的值。
H’,W’ 分別為輸出Feature Map的高和寬。當 H’=H 並且 W’=W 時，則ST是正常的仿射變換，當 H’=H/2 並且 W’=W/2 時, 此時ST可以起到和池化類似的降取樣的功能。
以雙線性插值為例，插值過程即為：
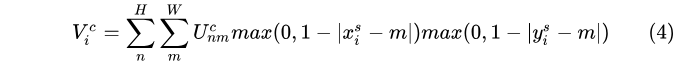
上式可以這麼理解：遍歷整個輸入Feature Map，如果遍歷到的點 (n,m) 距離大於1，即 |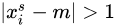
，那麼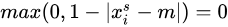 
（ n 處同理），即只有距離 
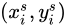最近的四個點參與計算。且距離與權重成反比，也就是距離越小，權值越大，也就是雙線性插值的過程，如圖3。其中 
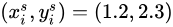，則：
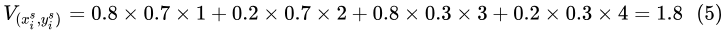
圖3：STN中的雙線性插值示例
上式中的幾個值都是可偏導的:
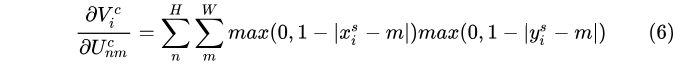
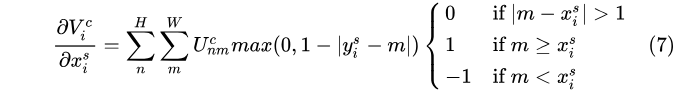
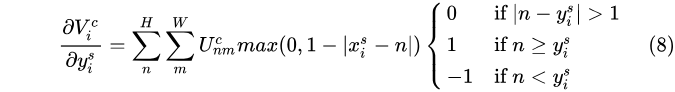
再對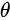 
求導為:
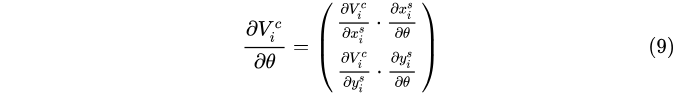
ST的可導帶來的好處是其可以和整個卷積網路一起端到端的訓練，能夠以layer的形式直接插入到卷積網路中。
- STN
1.3節中介紹過，將ST插入到卷積網路中便得到了STN，在插入ST的時候，需要注意以下幾點：
在輸入影象之後接一個ST是最常見的操作，也是最容易理解的，即自動影象矯正；
理論上講ST是可以以任意數量插入到網路中的任意位置，ST可以起到裁剪的作用，是一種高階的Attention機制。但多個ST無疑增加了網路的深度，其帶來的收益價值值得討論；
STM雖然可以起到降取樣的作用，但一般不這麼使用，因為基於ST的降取樣產生了對其的問題；
可以在同一個卷積網路中並行使用多個ST，但是一般ST和影象中的物件是 1:1 的關係，因此並不是具有非常廣泛的通用性。