閒扯：大資料不如小資料

這是一份很新的Paper(2015.6)，來自於Google旗下的新銳AI公司DeepMind的四位劍橋Phd研究員。

他們針對CNN的特點，構建了一個新的區域性網路層，稱為空間變換層，如其名，它能將輸入影象做任意空間變換。

大資料不如小資料，如果大資料不能被模型有效利用。

該現象是比較常見的，如ML實戰的一個經典問題：資料不均衡，這樣模型就會對大類資料過擬合，忽略小類資料。

將大資料按照難易度剖分，分批學習，要比直接全部硬塞有效得多。

當前，我們炙手可熱的模型仍然是蒟蒻的，而資料卻是巧奪天工、超乎想象的。

因而，想要通過模型完全摸清資料的Distribution是不現實的，發明、改良模型結構仍然是第一要務，

而不單純像Li Feifei教授劍走偏鋒，用ImageNet這樣的大資料推進深度學習程序。

空間變換的重要意義

[區域性性]、[平移不變性]、[縮小不變性]，還對缺失的[旋轉不變性]做了相應的實驗。

這些不變性的本質就是影象處理的經典手段，[裁剪]、[平移]、[縮放]、[旋轉]。

這些手段又屬於一個家族：空間變換，又服從於同一方法：座標矩陣的仿射變換。

那麼，神經網路是否有辦法，用一種統一的結構，自適應實現這些變換呢？DeepMind用一種簡易的方式實現了。

影象處理技巧：仿射矩陣、逆向座標對映、雙線性插值

1.1 仿射變換矩陣

實現[裁剪]、[平移]、[縮放]、[旋轉]

$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}$

—————————————————————————————————————————————————————————

對於平移操作，座標仿射矩陣為：

$\begin{bmatrix}1 & 0 & \theta_{13} \\ 0& 1 & \theta_{23}\end{bmatrix}\begin{bmatrix}x\\ y\\1\end{bmatrix}=\begin{bmatrix}x+\theta_{13}\\
y+\theta_{23}\end{bmatrix}$

—————————————————————————————————————————————————————————

對於縮放操作，座標仿射矩陣為：

$\begin{bmatrix}\theta_{11} & 0 & 0 \\ 0& \theta_{22} & 0\end{bmatrix}\begin{bmatrix}x\\ y\\1\end{bmatrix}=\begin{bmatrix}\theta_{11}x\\
\theta_{22}y\end{bmatrix}$

—————————————————————————————————————————————————————————

對於旋轉操作，設繞原點順時針旋轉$\alpha$度，座標仿射矩陣為：

$\begin{bmatrix}cos(\alpha) & sin(\alpha) & 0 \\ -sin(\alpha)& cos(\alpha) & 0\end{bmatrix}\begin{bmatrix}x\\ y\\1\end{bmatrix}=\begin{bmatrix}
cos(\alpha)x+sin(\alpha)y\\ -sin(\alpha)x+cos(\alpha)y\end{bmatrix}$

這裡有個trick，由於影象的座標不是中心座標系，所以只要做下Normalization，把座標調整到[-1,1]。

這樣，就繞影象中心旋轉了，下文中會使用這個trick。

—————————————————————————————————————————————————————————

至於裁剪操作，沒有看懂Paper的關於左2x2 sub-matrix的行列式值的解釋，但可以從座標範圍解釋：

只要$x^{'}$、$y^{'}$的範圍比$x$，$y$小，那麼就可以認為是目標圖定位到了源圖的區域性。

這種這種仿射變換沒有具體的數學形式，但肯定是可以在神經網路搜尋過程中使用的。

1.2 逆向座標對映

注：感謝網友@載重車提出疑問，修正了這部分的內容。具體請移步評論區。

★本部分作為一個對論文的錯誤理解，保留。

線上性代數計算中，一個經典的求解思路是：

$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}\begin{bmatrix}x^{Source}\\ y^{Source}\\ 1\end{bmatrix}=\begin{bmatrix}x^{Target}\\ y^{Target}\end{bmatrix}$

這種做法在做影象處理時，會給並行矩陣程式設計造成尷尬——需要犧牲額外的空間儲存對映源，：

由於$(x^{Target},y^{Target})$必然是離散的，當我們需要得到$Pixel(x^{Target},y^{Target})$的值時，

如果不及時儲存$(x^{Source},y^{Source})$，那麼就必須即時單點複製$Pixel(x^{Source},y^{Source})->Pixel(x^{Target},y^{Target})$

顯然，這種方法的實現依賴於$For$迴圈：

$For(0....i....Height)\\ \quad For(0....j....Width) \\ \quad \quad Calculate\&Copy$

為了能讓矩陣平行計算成為可能，我們需要逆轉一下思路：

$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{'}\begin{bmatrix}x^{Target}\\ y^{Target}\\ 1\end{bmatrix}=\begin{bmatrix}x^{Source}\\ y^{Source}\end{bmatrix}$

之後，構建變換目標圖就轉化成了，陣列下標取元素問題：

$PixelMatrix^{Target}=PixelMatrix^{Source}[x^{Source},y^{Source}]$

這依賴於仿射矩陣的一個性質：

$\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{'}=\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{-1}$

即，由Target變換為Source時，新仿射矩陣為源仿射矩陣的逆矩陣。

1.3 雙線性插值

考慮一個$[1,10]$影象放大10倍問題，我們需要將10個畫素，擴充套件到為100的數軸上，整個影象應該有100個畫素。

但其中90個對應Source圖的座標是非整數的，是不存在的，如果我們用黑色($RGB(0,0,0)$)填充，此時影象是慘不忍睹的。

所以需要對缺漏的畫素進行插值，利用影象資料的區域性性近似原理，取鄰近畫素做平均生成。

雙線性插值是一個兼有質量與速度的方法(某些電子遊戲裡通常這麼排列：線性插值、雙線性插值....):

如果$(x^{Source},y^{Source})$是實數座標，那麼先取整(截尾)，然後沿軸擴充套件$d$個座標單位，得到$P_{21}$、$P_{12}$、$P_{22}$

一般的(原始碼中)，取$d=1$，式中分母全被消去，再利用圖中雙線性插值式進行插值，得到$Pixel(x^{Source},y^{Source})$的近似值。

神經網路

2.1 塊狀神經元

CNN是一個變革的先驅者模型，它率先提出區域性連線觀點，減少網路廣度，增加網路深度。

區域性連線讓神經元呈塊狀，單引數成引數組；讓網路2D化，切合2D影象；讓權值共享，大幅度減少引數量。

仿射矩陣自適應學習理論，因此而得以實現：

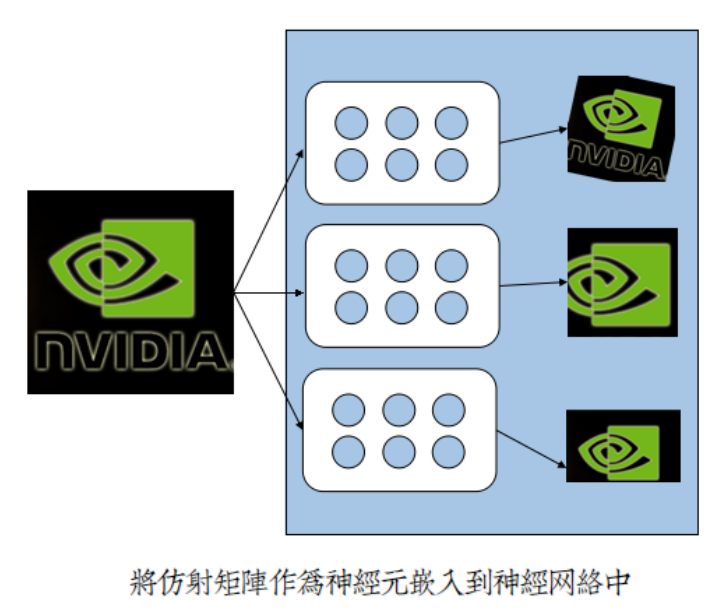
2.2 基本結構與前向傳播

論文中的結構圖描述得不是很清楚，個人做了部分調整，如下：

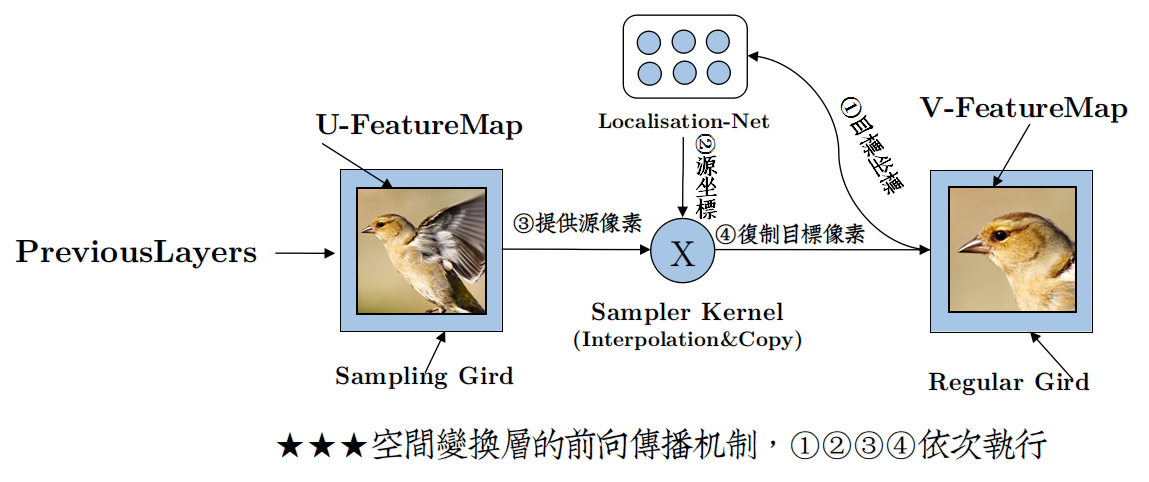
DeepMind為了描述這個空間變換層，首先添加了座標網格計算的概念，即：

對應輸入源特徵影象素的座標網格——Sampling Grid，儲存著$(x^{Source},y^{Source})$

對應輸出源特徵影象素的座標網格——Regluar Grid  ，儲存著$(x^{Target},y^{Target})$

然後，將仿射矩陣神經元組命名為定位網路 (Localisation Network)。

對於一次神經元提供引數，座標變換計算，記為 $\tau_{\theta}(G)$，根據1.2，有:

$\tau_{\theta}(G_{i})=\begin{bmatrix}\theta_{11} & \theta_{12} & \theta_{13} \\ \theta_{21}& \theta_{22} & \theta_{23}\end{bmatrix}^{'}\cdot\begin{bmatrix}x_{i}^{Target}\\ y_{i}^{Target}\\ 1\end{bmatrix}=\begin{bmatrix}x_{i}^{Source}\\ y_{i}^{Source}\end{bmatrix}\quad where \quad i=1,2,3,4..,H*W$

該部分對應於圖中的①②，但是與論文中的圖有些變化，可能是作者並沒有將逆向計算的Trick搬到結構圖中來。

所以你看到的仍然是Sampling Grid提供座標給定位網路，而具體實現的時候恰好是相反的，座標由Regluar Grid提供。

————————————————————————————————————————————————————————

Regluar Grid提供的座標組是順序逐行掃描座標的序列，序列長度為 $[Heght*Width]$，即：

將2D座標組全部1D化，根據在序列中的位置即可立即算出，在Regluar Grid中位置。

這麼做的最大好處在於，無須額外儲存Regluar Grid座標$(x^{Target},y^{Target})$。

因為從輸入特徵圖$U$陣列中，按下標取出的新畫素值序列，仍然是逐行掃描順序，簡單分隔一下，便得到了輸出特徵圖$V$。

該部分對應於圖中的③。

————————————————————————————————————————————————————————

(1.3)中提到了，直接簡單按照$(x^{Source},y^{Source})$，從源畫素陣列中複製畫素值是不可行的。

因為仿射變換後的$(x^{Source},y^{Source})$可以為實數，但是畫素位置座標必須是整數。

為了解決畫素值缺失問題，必須進行插值。插值核函式很多，原始碼中選擇了論文中提供的第二種插值方式——雙線性插值。

(1.3)的插值式非常不優雅，DeepMind在論文利用max與abs函式，改寫成一個簡潔、優雅的插值等式：

$V_{i}^{c}=\sum _{n}^{H}\sum _{m}^{W}U_{nm}^{c}\max(0,1-|x_{i}^{S}-m|)\max(0,1-|y_{i}^{S}-n|) \quad where \quad i\in [1,H^{'}W^{'}],c\in[1,3]$

兩個 $\sum$ 實際上只篩出了四個鄰近插值點，雖然寫法簡潔，但白迴圈很多，所以原始碼中選擇了直接算4個點，而不是用迴圈篩。

該部分對應圖中的④。

2.3 梯度流動與反向傳播

新增空間變換層之後，梯度流動變得有趣了，如圖：

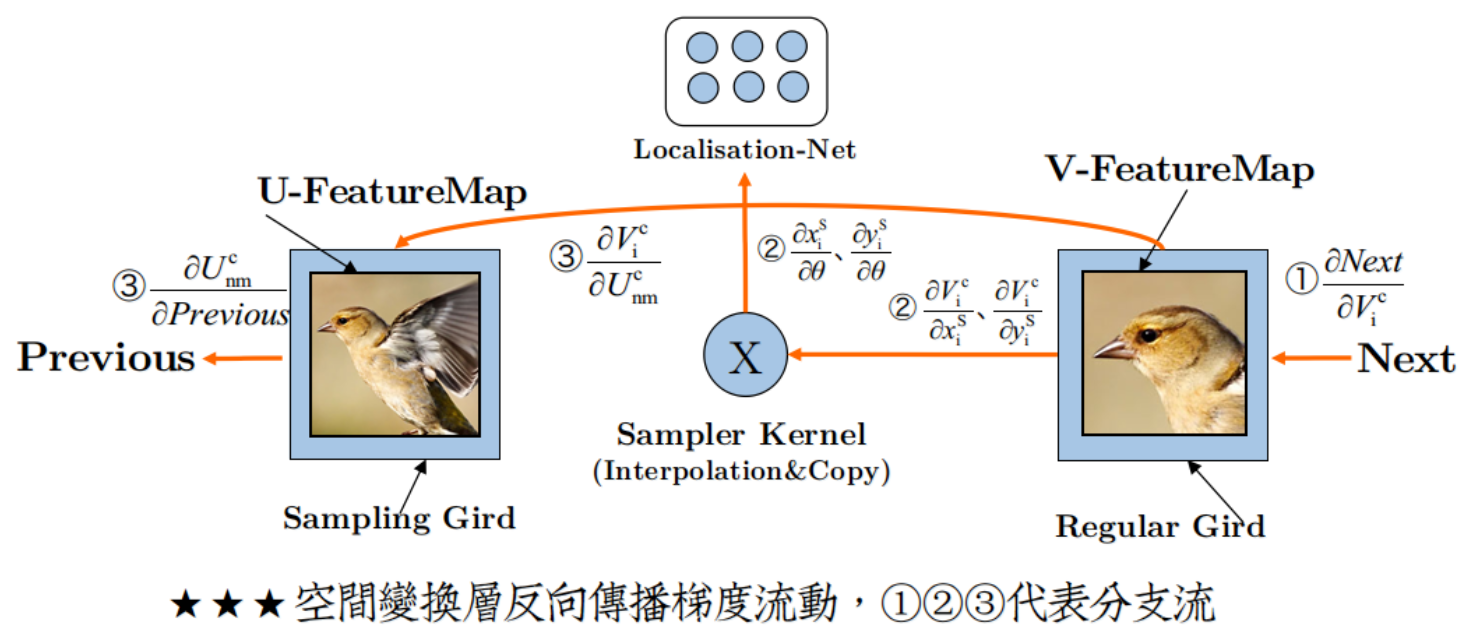
形成了三股分支流：

(I)後の流：

$ErrorGradient\rightarrow .....\rightarrow \frac{\partial Next}{\partial V_{i}^{c}}$

這是Back Propagation從後層繼承的動力源泉，沒有它，你就不可能完成Back Propagation。

(II)裡の流：

$\left\{\begin{matrix}\frac{\partial V_{i}^{c}}{\partial x_{i}^{S}}\rightarrow \frac{\partial x_{i}^{S}}{\partial \theta}\\ \frac{\partial V_{i}^{c}}{\partial y_{i}^{S}}\rightarrow \frac{\partial y_{i}^{S}}{\partial \theta}\end{matrix}\right.$

個人對這股流的最好描述就是：一江春水流進了小黑屋。

是的，你沒有看錯，這股流根本就沒有流到網路開頭，而是在定位網路處就斷流了。

由此來看，定位網路就好像是在主網路旁側偷建的小黑屋，是一個違章建築。

所以也無怪乎作者說，定位網路直接變成了一個迴歸模型，因為更新完引數，流就斷了，獨立於主網路。

(III)前の流：

$\frac{\partial V_{i}^{c}}{\partial U_{nm}^{i}}\rightarrow\frac{\partial U_{nm}^{i}}{\partial Previous}$

這是Back Propagation傳宗接代的根本保障，沒有它，Back Propagation就斷子絕孫了。

2.4* 區域性梯度

論文中多次出現[區域性梯度](Sub-Gradient) 的概念。

作者們反覆強調，他們寫的，優雅簡潔的取樣核函式，是不連續的，不能如下直接求導：

$g=\frac{\partial V_{i}^{c}}{\partial \theta}$

而應該是分兩步，先對$x_{i}^{S}$ 、$x_{i}^{S}$ 求區域性梯度: $\frac{\partial V_{i}^{c}}{\partial x_{i}^{c}}$ 、$\frac{\partial V_{i}^{c}}{\partial y_{i}^{c}}$，後有：

$\left\{\begin{matrix}g=\frac{\partial V_{i}^{c}}{\partial x_{i}^{S}} \cdot \frac{\partial x_{i}^{S}}{\partial \theta}\\ g=\frac{\partial V_{i}^{c}}{\partial y_{i}^{S}} \cdot \frac{\partial y_{i}^{S}}{\partial \theta}\end{matrix}\right.$

有趣的是，對於Theano這種自動求導的Tools，區域性梯度可以直接被忽視。

因為Theano的Tensor機制，會聰明地討論並且解離非連續函式，追蹤每一個可導子式，即便你用了作者們的優雅的取樣函式，

Tensor.grad函式也能精確只對篩出的4個點求導，所以在Theano裡討論非連續函式和區域性梯度，是會被貽笑大方的。