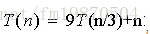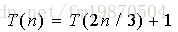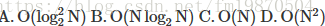一直以來時間複雜度都不會算嗚嗚嗚，今天理一理

證明咱就算了，沒這腦子。對於第一種情況，舉幾個栗子：

1）例1：二叉樹的遍歷。

           T(n)=2T (n/2)+Θ (1) 。

           其中(a=2), (b=2), (f(n)=1), 此時(ϵ=1)。

           所以 (T(n)=Θ(n)) 。

2）例1：歸併排序。

           T(n)=2T(n/2 )+Θ(n)  。

           其中(a=2), (b=2), (f(n)=n)，此時(k=0)。

           所以T(n)=Θ(nlog 2 n)

     例2：二分搜尋（折半搜尋）。

           T(n)=T(n/2 )+Θ(1)  。

           其中(a=1), (b=2), (f(n)=1), 此時(k=0),

           所以T(n)=Θ(log 2 n)。

3）沒栗子了...

例題解析

1）

        第一步：列出a=9,b=3,f(n)=n;

        第二步：計算=；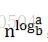

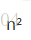
        第三步：與f(n)比較，發現是第一種情況，代入計算，答案T(n)=Θ(n^2)；

2）

         第一步：列出a=1,b=2/3,f(n)=1;

         第二步：計算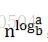=1；

         第三步：與f(n)比較，發現是第二種情況，代入計算，答案T(n)=Θ(logn)；

3)

    【NOIP2015初賽】某演算法的計算時間表示為遞推關係式：

     T(N)=T(N−1)+N, T(0)=1。則該演算法的時間複雜度為______________________________________________________。

    【解析】難道這個就要用主定理了？容易推匯出T(n)=T(0)+1+...+n=1+n∗(n+1)/2,   則時間複雜度為O(n^2 ) ，選D