關於kruskal與prim演算法在題目中的運用
一般來說,能用prim做的題目,一般用kruskal也能做,而且複雜度更低,而kruskal能做的題prim有可能解決不了,但是在我今天做的題目發現其實在某些時刻還是應該選用prim而不是kruskal,題目如下
P1991 無線通訊網
國防部計劃用無線網路連線若干個邊防哨所。2 種不同的通訊技術用來搭建無線網路;
每個邊防哨所都要配備無線電收發器;有一些哨所還可以增配衛星電話。
任意兩個配備了一條衛星電話線路的哨所(兩邊都ᤕ有衛星電話)均可以通話,無論他們相距多遠。而只通過無線電收發器通話的哨所之間的距離不能超過 D,這是受收發器的功率限制。收發器的功率越高,通話距離 D 會更遠,但同時價格也會更貴。
收發器需要統一購買和安裝,所以全部哨所只能選擇安裝一種型號的收發器。換句話說,每一對哨所之間的通話距離都是同一個 D。你的任務是確定收發器必須的最小通話距離 D,使得每一對哨所之間至少有一條通話路徑(直接的或者間接的)。
輸入輸出格式
輸入格式:
從 wireless.in 中輸入資料第 1 行,2 個整數 S 和 P,S 表示可安裝的衛星電話的哨所數,P 表示邊防哨所的數量。接下里 P 行,每行兩個整數 x,y 描述一個哨所的平面座標(x, y),以 km 為單位。
輸出格式:
輸出 wireless.out 中
第 1 行,1 個實數 D,表示無線電收發器的最小傳輸距離,精確到小數點後兩位。
輸入輸出樣例
輸入樣例#1: 複製
2 4 0 100 0 300 0 600 150 750
輸出樣例#1: 複製
212.13
說明
對於 20% 的資料:P = 2,S = 1
對於另外 20% 的資料:P = 4,S = 2
對於 100% 的資料保證:1 ≤ S ≤ 100,S < P ≤ 500,0 ≤ x,y ≤ 10000。
// luogu-judger-enable-o2 #include<iostream> #include<cmath> #include<vector> #include<algorithm> using namespace std; vector<double> v; struct Node{ int x, y; int cnt; }node[510]; struct edge{ int u, v; double cost; }E[250010]; bool cmp(edge a, edge b) { return a.cost < b.cost; } int father[510]; int findFather(int x) { while (x != father[x]) { x = father[x]; } return x; } int kruskal(int n, int m) { int Num_Edge = 0; for (int i = 0; i < n; i++) { father[i] = i; } sort(E, E + m, cmp); for (int i = 0; i < m; i++) { int faU = findFather(E[i].u); int faV = findFather(E[i].v); if (faU != faV) { father[faU] = faV; v.push_back(E[i].cost); Num_Edge++; if (Num_Edge == n - 1) break; } } if (Num_Edge != n - 1) return -1; else return 1; } int main() { int s, p; cin >> s >> p; for (int i = 0; i < p; i++) { cin >> node[i].x >> node[i].y; node[i].cnt = i; } int cnt = 0; for (int i = 0; i < p; i++) { for (int j = i + 1; j < p; j++) { double dis = sqrt(pow(node[i].x - node[j].x, 2) + pow(node[i].y - node[j].y, 2)); E[cnt].u = node[i].cnt; E[cnt].v = node[j].cnt; E[cnt++].cost = dis; } } kruskal(p, cnt); printf("%.2f", v[v.size() - s]); return 0; }
思考:關於這道題目其實爭議挺多的,有人說要刪除邊啥的,有人是用瓶頸生成樹來做的,不過我感覺我的這種思路算是比較大眾的思路,就是一個kruskal一套下來,然後貪心從後往前取就可以了,在這裡我使用了結構體來處理座標的問題,直接把他轉換成了一個結點,然後按照常規的套路來便可以了,然而接下來看下一道題目
P1265 公路修建
某國有n個城市,它們互相之間沒有公路相通,因此交通十分不便。為解決這一“行路難”的問題,政府決定修建公路。修建公路的任務由各城市共同完成。
修建工程分若干輪完成。在每一輪中,每個城市選擇一個與它最近的城市,申請修建通往該城市的公路。政府負責審批這些申請以決定是否同意修建。
政府審批的規則如下:
(1)如果兩個或以上城市申請修建同一條公路,則讓它們共同修建;
(2)如果三個或以上的城市申請修建的公路成環。如下圖,A申請修建公路AB,B申請修建公路BC,C申請修建公路CA。則政府將否決其中最短的一條公路的修建申請;

(3)其他情況的申請一律同意。
一輪修建結束後,可能會有若干城市可以通過公路直接或間接相連。這些可以互相:連通的城市即組成“城市聯盟”。在下一輪修建中,每個“城市聯盟”將被看作一個城市,發揮一個城市的作用。
當所有城市被組合成一個“城市聯盟”時,修建工程也就完成了。
你的任務是根據城市的分佈和前面講到的規則,計算出將要修建的公路總長度。
輸入輸出格式
輸入格式:
第一行一個整數n,表示城市的數量。(n≤5000)
以下n行,每行兩個整數x和y,表示一個城市的座標。(-1000000≤x,y≤1000000)
輸出格式:
一個實數,四捨五入保留兩位小數,表示公路總長。(保證有惟一解)
輸入輸出樣例
輸入樣例#1: 複製
4 0 0 1 2 -1 2 0 4
輸出樣例#1: 複製
6.47
說明
修建的公路如圖所示: 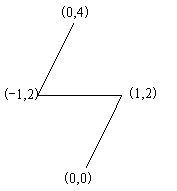
思考:看到這個題目是不是感覺特別熟悉有木有,感覺就是和上面那個題目一模一樣,就是換了個法子問你,然後我就把上面的程式碼稍微做了修改,然後把樣例輸了一遍,過了,然後我信心滿滿的交了上去,有倆個測試點記憶體不夠,然後我就開始吧int改成long long各種改,大概過了30分鐘還是沒有頭緒,後來看了別人的部落格才知道如果矩陣開到5000*5000是會記憶體超限的,我竟然糊塗到把這個都忘了,那麼問題來了,接下來要怎麼修改,這個時候我們仔細看一下題目就會發現,這是一個稠密圖,也就是點少邊多,完全適用於prim演算法,而且還可以直接用矩陣來儲存點的值,接下來直接上程式碼
// luogu-judger-enable-o2
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
const int MAXV = 5010;
int p[MAXV][2];
const int INF = 1e9;
double d[MAXV];
bool vis[MAXV];
double dist(int x1,int y1,int x2,int y2)
{
return sqrt((double)(x1-x2)*(x1-x2)+(double)(y1-y2)*(y1-y2));
}
int main() {
int n;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> p[i][0] >> p[i][1];
}
double ans = 0;
fill(d, d + MAXV, INF);
d[0] = 0;
for (int i = 0; i < n; i++) {
int u = -1;
double Min = INF;
for (int j = 0; j < n; j++) {
if (d[j] < Min && vis[j] == false) {
Min = d[j];
u = j;
}
}
vis[u] = true;
ans += d[u];
for (int v = 0; v < n; v++) {
double t=dist(p[u][0],p[u][1],p[v][0],p[v][1]);
if (t < d[v]){
d[v] = t;
}
}
}
printf("%.2f", ans);
return 0;
}
那麼問題又來了,既然這個題目可以用prim,那麼上一個題應該也是可以用prim來做的,事實上就是如此,這個題目真是一個比較好的教訓,以後還是要根據實際情況來使用相對應的演算法
