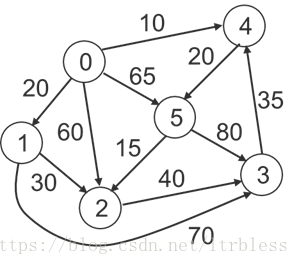
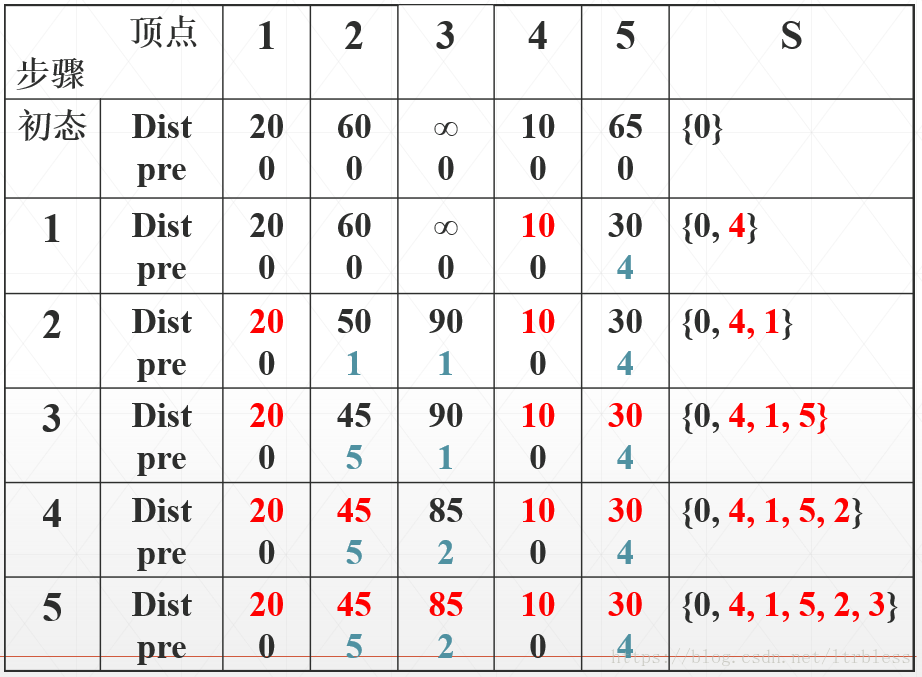
最短路問題(三種演算法與路徑還原演算法)
1、Bellman-Ford演算法:
用Bellman-Ford演算法求解單源最短路徑問題,單源最短路徑是指固定一個起點,求它到其他所有點的最短路問題。
struct edge { int from, to, cost; //從頂點from指向頂點to的權值為cost的邊 }; edge es[MAX_E]; //邊 int d[MAX_V]; //到出發點的最短距離 int V, E; //V是頂點數,E是邊數 //求解從頂點s出發到所有點的最短距離 void shortest_path(int s) { for(int i = 0; i < V; i++) d[i] = INF; d[s] = 0; while(true){ bool update = false; //判斷是否更新結束 for(int i = 0; i < E; i++){ //遍歷每一條邊 edge e = es[i]; if(d[e.from] != INF && d[e.to] > d[e.from] + e.cost){ // d[e.from] != INF 是判斷e.from這一點是否之前更新過,如果不加也行,因為如果 // d[e.from] == INF 則d[e.to] > d[e.from] + e.cost也一定不會成立,如果 // d[e.to] > d[e.from] + e.cost成立,那麼則需要更新節點 d[e.to] = d[e.from] + e.cost; update = true; //判斷是否更新結束 } } if(!update) break; //判斷是否更新結束 } }
該演算法是以邊為基礎的,如果在圖中不存在從起點可達的負圈(負圈的意思就是,有路徑上的權值為負數,一旦有負數存在,那麼會不斷的迭代更新,因為有負數所有權值可以一直減小。)那麼最短路不會經過同一個頂點兩次(也就是說,最多通過|V|-1條邊),while(true)迴圈最多執行|V| - 1次,因此複雜度為o(V·E)。
反之,如果存在從s可達的負圈,那麼在第|V|次迴圈中也會更新d的值,因此可以利用這個性質來檢查負圈。程式碼:
//如果返回True則存在負圈 bool find_negative_loop() { memset(d, 0, sizeof(d)); //把所有初始距離設定為0,檢測是否有負圈, //其實就是檢測一共有幾次迴圈,是否可以在第|V| - 1次迴圈那裡停止。 for(int i = 1; i <= V; i++){ for(int j = 0; j < E; j++){ edge e = es[j]; if(d[e.from] > d[e.to] + e.cost){ d[e.from] = d[e.to] + e.cost; if(i == V) return true; //第V次仍然更新了,則存在負圈。 } } } return false; }
2、Dijkstra演算法:
主要對點進行操作,使用的是鄰接矩陣實現的,時間複雜度為o(|V|^2)。
int cost[MAX_V][MAX_V]; //cost[u][v]表示邊e=(u, v)的權值(不存在這條邊時設為INF) int d[MAX_V]; //從頂點s出發的最短距離 bool used[MAX_V]; //已經使用過的圖中的點 int V; //頂點數 //從s出發到各個頂點的距離 void dijkstra(int s) { fill(d, d + V, INF); //初始化 fill(used, used + V, false); //初始化 d[s] = 0; while(true) { int v = -1; for(int u = 0; u < V; u++){ if(!used[u] && (v == -1 || d[u] < d[v])) v = u; // 從尚未使用過的頂點中選擇一個距離最小的頂點 } if(v == -1) break; //沒有可跟新的了,結束 used[v] = true; for(int u = 0; u < V; u++){ d[u] = min(d[u], d[v] + cost[u][v]); //因為加入了一個點V所以所有的d都要再更新一遍 } } }
優化:用STL裡面的priority_queue實現:
需要優化的是數值的插入(更新)和取出最小值,兩個操作,所以可以用堆來維護每個頂點當前最短距離。在更新最短距離的時候,把對應的元素往根的方向上移動以滿足堆的性質,而每次從堆中取出的最小值就是下次使用的頂點,這樣堆中元素一共o(V)個,更新和取出的操作有o(E)次,因此整個演算法的時間複雜度為:o(E · logV). 所以下面將用優點佇列來實現。
優先佇列知識補充: priority_queue<Type, Container, Functional> Type為資料型別, Container為儲存資料的容器,Functional為元素比較方式。 如果不寫後兩個引數,那麼容器預設用的是vector,比較方式預設用operator<,也就是優先佇列是大頂堆,隊頭元素最大。
struct edge
{
int to, cost;
};
typedef pair<int, int> P;
//因為pair定義了自己的排序規則,即先按照第一維,當第一維相同時,才比較第二維;
//所以這裡定義的P 的 first 代表是最短距離 second 代表是頂點的編號;
int V; //頂點數
vector<edge> G[MAX_V]; //
int d[MAX_V];
void dijkstra(int s)
{
priority_queue<P, vector<P>, greater<P>> que;
fill(d, d + V, INF);
d[s] = 0;
que.push(P(0, s));
while(!empty(que)){
P p = que.top(); //取堆頂元素
que.pop();
int v = p.second;
if(d[v] < p.first) continue; //當取出的最小值不是最短距離,則丟棄該值
for(int i = 0; i < G[v].size; i++){ //把與v相連的所有的頂點都跟新一遍
edge e = G[v][i];
if(d[e.to] > d[v] + e.cost){
d[e.to] = d[v] + e.cost;
que.push_back(P(d[e.to], e.to));
}
}
}
}
相對於Bellman-Ford的o(|V||E|)的複雜度,Dijkstra演算法的複雜度是o(|E|log|V|),可以更高效的計算最短路的長度。但是,如果說圖中存在負邊的情況下,Dijkstra演算法就無法正確求解問題,還是需要Bellman-Ford演算法。
3、Floyd-Warshall演算法:
int d[MAX_V][MAX_V];
int V;
void waeshall_floyd()
{
for(int k = 0; k < V; k++){
for(int i = 0; i < V; i++){
for(int j = 0; j < V; j++){
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}直接遍歷,求解各個點之間的最短路徑,簡單易懂。它還可以處理邊是負數的情況。判斷圖中是否存在負圈,只需要檢查是否存在d[ i ][ i ]是負數的頂點 i 就夠了。
路徑還原:
前三個演算法都是求解最終距離的,這裡說一下,如果需要輸出路徑怎麼辦。 可以用一個prev[ j ]來記錄最短路上頂點 j 的前驅,那麼在o(|V|)的時間內完成最短路徑的恢復。在d[ j ]被d[ j ] = d[ k ] + cost[ k ][ j ]更新時,修改prev[ j ] = k,這樣就可以求出來prev的陣列,可以在以上演算法中用路徑前驅標記法來還原出來路徑。 這裡給出dijkstra演算法的路徑還原演算法程式碼:
int cost[MAX_V][MAX_V]; //cost[u][v]表示邊e=(u, v)的權值(不存在這條邊時設為INF)
int d[MAX_V]; //從頂點s出發的最短距離
bool used[MAX_V]; //已經使用過的圖中的點
int V; //頂點數
int prev[MAX_V]; //記錄前驅點
//從s出發到各個頂點的距離
void dijkstra(int s)
{
fill(d, d + V, INF); //初始化
fill(used, used + V, false); //初始化
fill(prev, prev + V, -1);
d[s] = 0;
while(true)
{
int v = -1;
for(int u = 0; u < V; u++){
if(!used[u] && (v == -1 || d[u] < d[v])) v = u;
// 從尚未使用過的頂點中選擇一個距離最小的頂點
}
if(v == -1) break; //沒有可跟新的了,結束
used[v] = true;
for(int u = 0; u < V; u++){
d[u] = min(d[u], d[v] + cost[u][v]); //因為加入了一個點V所以所有的d都要再更新一遍
prev[u] = v;
}
}
}
vector<int> get_path(int t) //到頂點t的最短路
{
vector<int> path;
for(; t != -1; t = prev[t])
path.push_back(t);
reverse(path.begin(), path.end());
return path;
}