一：Floyd-Warshall演算法

直接貼出程式碼

#include <stdio.h>
int main()
{
    int e[10][10],k,i,j,n,m,t1,t2,t3;
    int inf=99999999; //用inf(infinity的縮寫)儲存一個我們認為的正無窮值,只要比題目所給任意數大就行 
    //讀入n和m，n表示頂點個數，m表示邊的條數
    scanf("%d %d",&n,&m);

    //初始化
    for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
            if(i==j) e[i][j]=0;
              else e[i][j]=inf;
    //讀入邊
    for(i=1;i<=m;i++)
    {
        scanf("%d %d %d",&t1,&t2,&t3);
        e[t1][t2]=t3;
    }

    //Floyd-Warshall演算法核心語句
    for(k=1;k<=n;k++)
        for(i=1;i<=n;i++)
            for(j=1;j<=n;j++)
                if(e[i][j]>e[i][k]+e[k][j] )
                    e[i][j]=e[i][k]+e[k][j];

    //輸出最終的結果
    for(i=1;i<=n;i++)
    {
     for(j=1;j<=n;j++)
        {
            printf("%10d",e[i][j]);
        }
        printf("\n");
    }

    return 0;
}//求多源最短路 //鄰接矩陣的方法，輸出的是任意兩點的距離矩陣 
 

二：spfa演算法：是bellman演算法的優化寫法，用鄰接連結串列和棧來寫

求的是給定起點到任意點的帶負權最短路

適用範圍：給定的圖存在負權邊，這時類似Dijkstra等演算法便沒有了用武之地，而Bellman-Ford演算法的複雜度又過高，SPFA演算法便派上用場了。 我們約定有向加權圖G不存在負權迴路，即最短路徑一定存在。當然，我們可以在執行該演算法前做一次拓撲排序，以判斷是否存在負權迴路，但這不是我們討論的重點。

演算法思想：我們用陣列d記錄每個結點的最短路徑估計值，用鄰接表來儲存圖G。我們採取的方法是動態逼近法：設立一個先進先出的佇列用來儲存待優化的結點，優化時每次取出隊首結點u，並且用u點當前的最短路徑估計值對離開u點所指向的結點v進行鬆弛操作，如果v點的最短路徑估計值有所調整，且v點不在當前的佇列中，就將v點放入隊尾。這樣不斷從佇列中取出結點來進行鬆弛操作，直至佇列空為止

期望的時間複雜度O(ke)， 其中k為所有頂點進隊的平均次數，可以證明k一般小於等於2。

實現方法：

　　建立一個佇列，初始時佇列裡只有起始點，再建立一個表格記錄起始點到所有點的最短路徑（該表格的初始值要賦為極大值，該點到他本身的路徑賦為0）。然後執行鬆弛操作，用佇列裡有的點作為起始點去重新整理到所有點的最短路，如果重新整理成功且被重新整理點不在佇列中則把該點加入到佇列最後。重複執行直到佇列為空。

判斷有無負環：
　　如果某個點進入佇列的次數超過N次則存在負環（SPFA無法處理帶負環的圖）

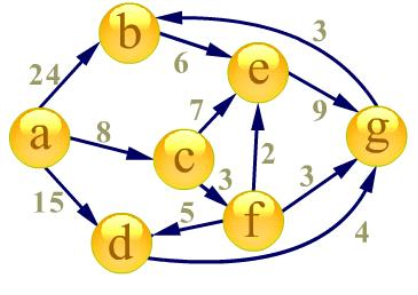
首先建立起始點a到其餘各點的
最短路徑表格

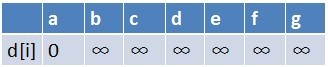
首先源點a入隊，當佇列非空時：
　１、隊首元素（a）出隊，對以a為起始點的所有邊的終點依次進行鬆弛操作（此處有b,c,d三個點），此時路徑表格狀態為：

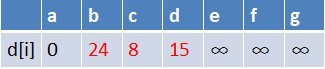
在鬆弛時三個點的最短路徑估值變小了，而這些點佇列中都沒有出現，這些點
需要入隊，此時，佇列中新入隊了三個結點b,c,d

隊首元素b點出隊，對以b為起始點的所有邊的終點依次進行鬆弛操作（此處只有e點），此時路徑表格狀態為：

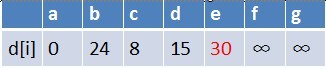
在最短路徑表中，e的最短路徑估值也變小了，e在佇列中不存在，因此e也要
入隊，此時佇列中的元素為c，d，e

隊首元素c點出隊，對以c為起始點的所有邊的終點依次進行鬆弛操作（此處有e,f兩個點），此時路徑表格狀態為：

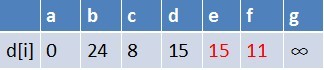
在最短路徑表中，e，f的最短路徑估值變小了，e在佇列中存在，f不存在。因此
e不用入隊了，f要入隊，此時佇列中的元素為d，e，f

 隊首元素d點出隊，對以d為起始點的所有邊的終點依次進行鬆弛操作（此處只有g這個點），此時路徑表格狀態為：

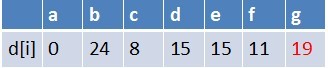
在最短路徑表中，g的最短路徑估值沒有變小（鬆弛不成功），沒有新結點入隊，佇列中元素為f，g

隊首元素f點出隊，對以f為起始點的所有邊的終點依次進行鬆弛操作（此處有d，e，g三個點），此時路徑表格狀態為：

在最短路徑表中，e，g的最短路徑估值又變小，佇列中無e點，e入隊，佇列中存在g這個點，g不用入隊，此時佇列中元素為g，e

隊首元素g點出隊，對以g為起始點的所有邊的終點依次進行鬆弛操作（此處只有b點），此時路徑表格狀態為：

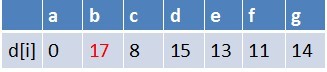
在最短路徑表中，b的最短路徑估值又變小，佇列中無b點，b入隊，此時佇列中元素為e，b
隊首元素e點出隊，對以e為起始點的所有邊的終點依次進行鬆弛操作（此處只有g這個點），此時路徑表格狀態為：

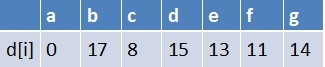
在最短路徑表中，g的最短路徑估值沒變化（鬆弛不成功），此時佇列中元素為b

隊首元素b點出隊，對以b為起始點的所有邊的終點依次進行鬆弛操作（此處只有e這個點），此時路徑表格狀態為：

在最短路徑表中，e的最短路徑估值沒變化（鬆弛不成功），此時佇列為空了

最終a到g的最短路徑為１４

#include<stdio.h>
#include<string.h>
#include<queue>
#include<algorithm>
using namespace std; 
#define MAXN 1000 
int first[MAXN];//first[i]記錄以i為起點的最後一條邊的儲存位置 
int next[MAXN];//next[i]記錄與i同起點的上一條邊的儲存位置 
int u[MAXN],v[MAXN],w[MAXN];
int dis[MAXN];//記錄起點到i的最長的距離 
int book[MAXN];//標記點 
int c[MAXN];//統計次數 
int n,m;//n為頂點,m為邊 
int flag;//標記 
int spfa(int s,int n){
	int i,j,k;
	queue<int > q;
	memset(dis,0x3f,sizeof(0x3f));
	dis[s]=0;
	memset(book,0,sizeof(book));
	memset(c,0,sizeof(c));
	q.push(s);
	book[s]=1;
	flag=0;
	while(!q.empty())
	{
		int x;
		x=q.front();
		q.pop();
		book[x]=0;//隊頭元素出隊，並且消除標記
		for(k=first[k] ; k!=-1 ; k=next[k])//遍歷頂點x的鄰接表
		{
			int y=v[k];
            if(dis[x]+w[k]<dis[y])
            {
                dis[y]=dis[x]+w[k];  //鬆弛
                if(!book[y])  //頂點y不在隊內
                {
                    book[y]=1;    //標記
                    c[y]++;      //統計次數
                    q.push(y);   //入隊
                    if(c[y]>n)  //超過入隊次數上限，說明有負環
                        return flag=0;
                }
            }
		}
	} 
}
int main()
{
	int x,y,z;
	while(~scanf("%d %d",&n , &m))
	{
		memset(first,-1,sizeof(first));
		for(int i=1 ; i<=m ; i++){
			scanf("%d %d %d",&u[i],&v[i],&w[i]);
			next[i]=first[u[i]];
			first[u[i]]=i;
		}
		spfa(1,n);
        if(flag)
            printf("有負權迴路\n");
        else
        {
            for(int i=1;i<=n;i++)
            	printf("%d ",dis[i]);
        }
	}
	return 0;
}
/* 
bellman演算法： 
for(int k=1;k<=n-1;k++)//進行n-1次鬆弛 
	for(int i=1;i<=m;i++)//列舉每一條邊 
		if(dis[v[i]]>dis[u[i]]+w[i])//嘗試鬆弛每一條邊 
			dis[v[i]]=dis[u[i]]+w[i]; 
*/ 

三：dijstra演算法：

求給定起點到任意點的最短路（不能有負權）

#include<stdio.h>
#include<string.h>
#define MAXN 1000 
#define INF 0x3f3f3f
int e[MAXN][MAXN];//存圖 
int dis[MAXN];//記錄起點到i的最長的距離 
int book[MAXN];//標記點 
int n,m;//n為頂點,m為邊
void dijstra(){
	int i,j,k,u,v;
	int flag;
	memset(book,0,sizeof(book));
	for(i=1 ; i<=m ; i++){
		dis[i]=e[1][i];
	}
	book[1]=1;
	for(i=1 ; i<=n-1 ; i++)
	{
		flag=INF;
		for(j=1 ; j<=n ; j++)//找到每個過程中距1最近的點 
		{
			if(book[j]==0 && dis[j]<flag)
			{
				flag=dis[j];
				u=j;
			}
		}
		book[u]=1;
		for(v=1 ; v<=n ; v++)//進行鬆弛，判斷是否經過轉折點使之更小 
		{
			if(e[u][v]<INF)
			{
				if(dis[v]>dis[u]+e[u][v])
					dis[v]=dis[u]+e[u][v];
			}
		}
	}
	for(i=1 ; i<=n ; i++)
	{
		printf("1->%d %d\n",i,dis[i]);//求的是以1為起點的最短路
	}
}
int main()
{
	int x,y,z;
	while(~scanf("%d %d",&n,&m))
	{
		for(int i=1 ; i<=n ; i++)
			for(int j=1 ; j<=n ; j++)
			{
				if(i == j)	e[i][j]=0;
				else	e[i][j]=INF;
			}
		for(int i=1 ; i<=m ; i++){
			scanf("%d %d %d",&x,&y,&z);
			e[x][y]=z;//有向圖 
		}
		dijstra();
	}
	return 0;
}