欠擬合 under fitting

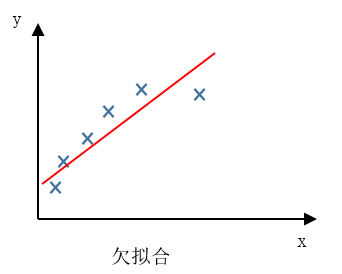
欠擬合(under fitting)，這個問題的另一個術語叫做 高偏差(High bias)。這兩種說法大致相似，意思是它沒有很好地擬合訓練資料。

過擬合 over fitting

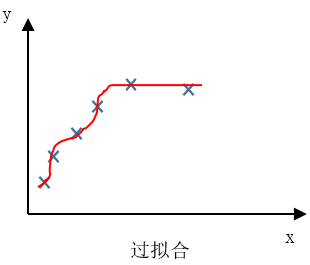
• 過度擬合(over fitting)，另一個描述該問題的術語是 高方差(High variance)。

• 過擬合的問題經常會在模型過度複雜或訓練資料較少時發生，導致模型無法泛化到新的資料樣本中。

• 泛化 (generalize) 指的是一個假設模型能夠應用到新樣本的能力。

• 正則化技術是保證演算法泛化能力的有效工具，參見： 正則化方法：資料增強、regularization、dropout

偏差與方差

學習演算法的預測誤差，或者說泛化誤差 (generalization error) 可以分解為三個部分: 偏差(bias)、方差(variance) 和噪聲(noise)。在估計學習演算法效能的過程中, 我們主要關注偏差與方差。因為噪聲屬於不可約減的誤差 (irreducible error)。

• 偏差（bias）：這裡的偏指的是偏離，描述的是預測值與標準值之間的差距。偏差越大，越偏離真實資料。 “標準” 也就是真實情況 (ground truth)，在分類任務中, 這個 “標準” 就是真實標籤 (label).

• 方差（variance）：描述的是預測值的變化範圍，離散程度，也就是預測值在標準值附近的波動程度。方差越大，資料的分佈越分散。

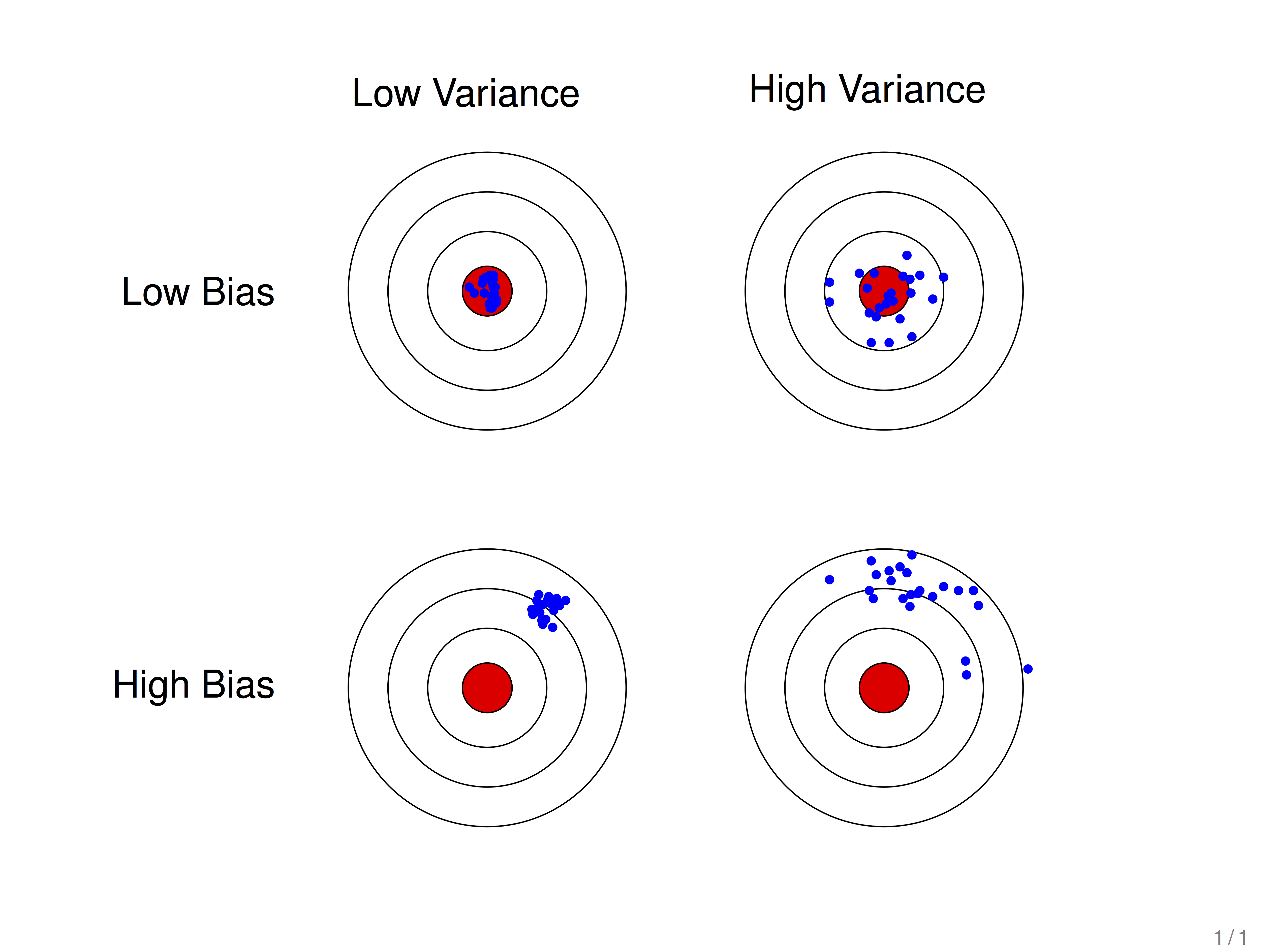
• 假設紅色的靶心區域是學習演算法的正確預測值，藍色點為訓練過程中模型對樣本的預測值，藍色點距離靶心越遠，預測效果越差。

• 藍色點比較集中時，方差比較小，比較分散時，方差比較大。

• 藍色點比較靠近紅色靶心時，偏差較小；遠離靶心時，偏差較大。

偏差-方差窘境 bias-variance dilemma

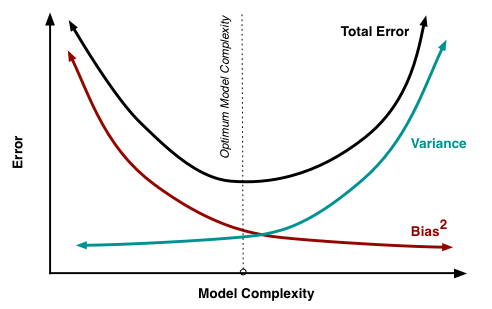
• 給定一個學習任務，在訓練初期由於訓練不足，學習器的擬合能力不夠強，偏差比較大，也是由於擬合能力不強，資料集的擾動也無法使學習器產生顯著變化，也就是欠擬合的情況。

• 隨著訓練程度的加深，學習器的擬合能力逐漸增強，訓練資料的擾動也能夠漸漸被學習器學到。

• 充分訓練後，學習器的擬合能力已非常強，訓練資料的輕微擾動都會導致學習器發生顯著變化，當訓練資料自身的、非全域性的特性被學習器學到了，則將發生過擬合。