密碼學及加密貨幣概述
1. 密碼學雜湊函式
- 特性1:碰撞阻力
定義:如果無法找到兩個值,x和y,x≠y,使得H(x)= H(y),則稱雜湊函式H具有碰
撞阻力。(這裡指的是無法找到,不代表不存在)。
應用:可用於判斷檔案是否被修改。由於具有碰撞阻力,被修改後的檔案的雜湊值肯定不等於未被修改的檔案的雜湊值。
- 特性2:隱祕性
定義:無法通過雜湊函式的輸出結果來確定輸入。
已知 H(nonce||msg),沒有可行方法找到msg。(nonce代表隨機值,在密碼學中術語中nonce指該值只能使用一次;||表示把一系列事件、事情聯絡起來)
- 特性3:謎題友好
定義:對於一個n位輸出值y,假定k選自高階最小熵分佈,如果無法找到一個可行的方法,在比2^n小很多時間內找到x,保證H(k||x)= y成立,則稱雜湊函式H為謎題友好。
應用:搜尋謎題,沒有一個解決策略會比隨機地嘗試x取值更好。比特幣挖礦也是這種思路。
- 安全雜湊演算法SHA - 256
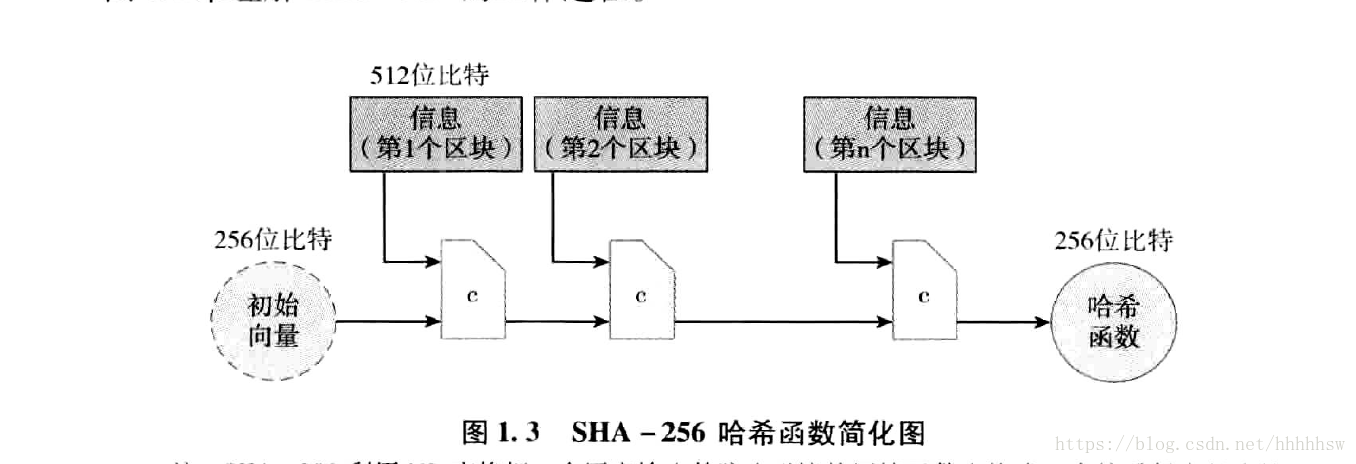
SHA - 256 是採用了MD(Merkle-Damgard)變換的雜湊函式,將只接受固定長度的雜湊函式轉化為可接受任意長度輸入的雜湊函式。
MD變換:如果壓縮函式的輸入為m位,輸出為n位。先將輸入的字串(可以為任意長度)分為長度位m-n的區塊,將每個區塊與之前的區塊的輸出一起代入壓縮函式,則輸入長度為(m-n)+n ,壓縮後輸出為n位。對於第一個區塊,我們需要選取一個初始向量。
如圖為SAH-256函式利用了一個輸入為768位、輸出為512位的壓縮函式來將一個輸入(可為任意長度)最終壓縮為256位的過程。
2. 雜湊指標及資料結構
定義:雜湊指標是一個指向資料儲存位置及其位置資料的雜湊值的指標。雜湊指標不但可以告訴你資料儲存的位置,還可以驗證資料是否被篡改過。
-
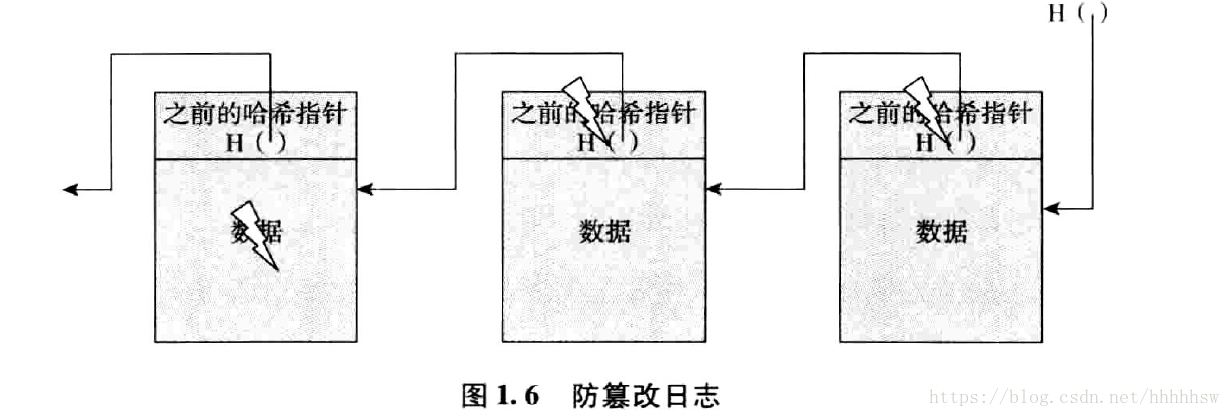
區塊鏈:通過雜湊指標而不是普通指標構建的一個連結串列。
如果第k個區塊的資料被修改,為了不被髮發現,需要繼續修改第K+1塊的雜湊指標,如此往復。所以我們只需要記住最新的雜湊指標,就可以確保整條鏈不被篡改。
-
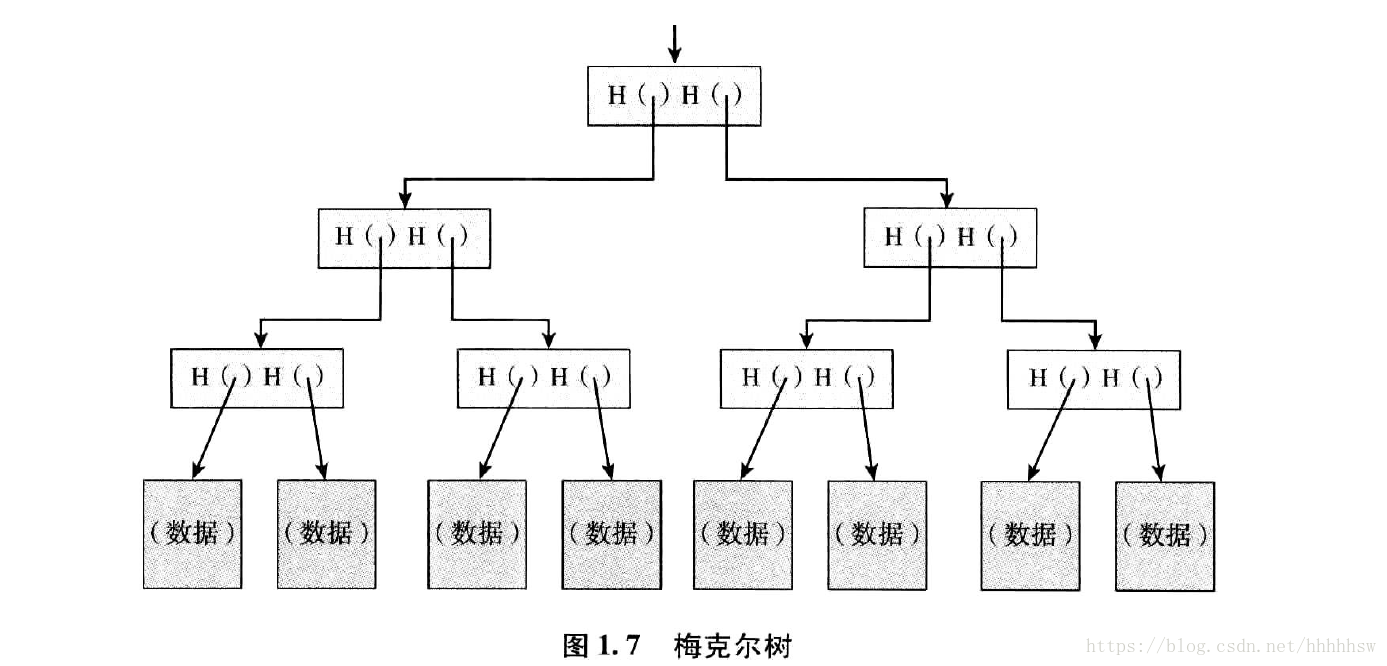
梅克爾樹:使用雜湊指標的二叉樹
將資料區塊兩兩分組,然後為每一組建立一個擁有兩個雜湊指標的資料結構,每個指標對應一個區塊,這些資料結構就構成了數的下一個層次,以此類推,最終我們得到樹根節點。我們只要記住樹根節點的雜湊指標就可以確保資料不被篡改。
3. 數字簽名
- 特性1:只有你可以製作你自己的簽名,但任何看到它的人都可以驗證其有效性
- 特性2:一個簽名只與一份特定的檔案發生聯絡,這個簽名不可以用於其他檔案,即不同檔案對應不同簽名。
演算法:
-
(sk,pk):=generateKeys(keysize) 通過generateKeys來產生私鑰sk和公鑰pk。私鑰被安全儲存,用於簽名;公鑰是人人都可以找到的,用於驗證簽名。
-
sig:=sign(sk,message)簽名過程就是把一段訊息和私鑰作為輸入,輸出即是簽名。
-
isValid:=verify(pk,message,sig)驗證過程就是把一段訊息和簽名和公鑰作為輸入,返回結果為真則證明簽名屬實,反之。
由於在實踐中你能夠簽署的資訊大小是有限制的,所以:
-
可以對資訊的雜湊值進行簽署
-
可以對雜湊指標進行簽署
比特幣使用的數字簽名方案是橢圓曲線數字簽名演算法(ECDSA),引數如下
4. 高飛幣
- 規則1:指定高飛可以隨時建立新幣,且這些新建立的幣都屬於他
- 規則2:擁有此幣的人可以將其轉給其他人
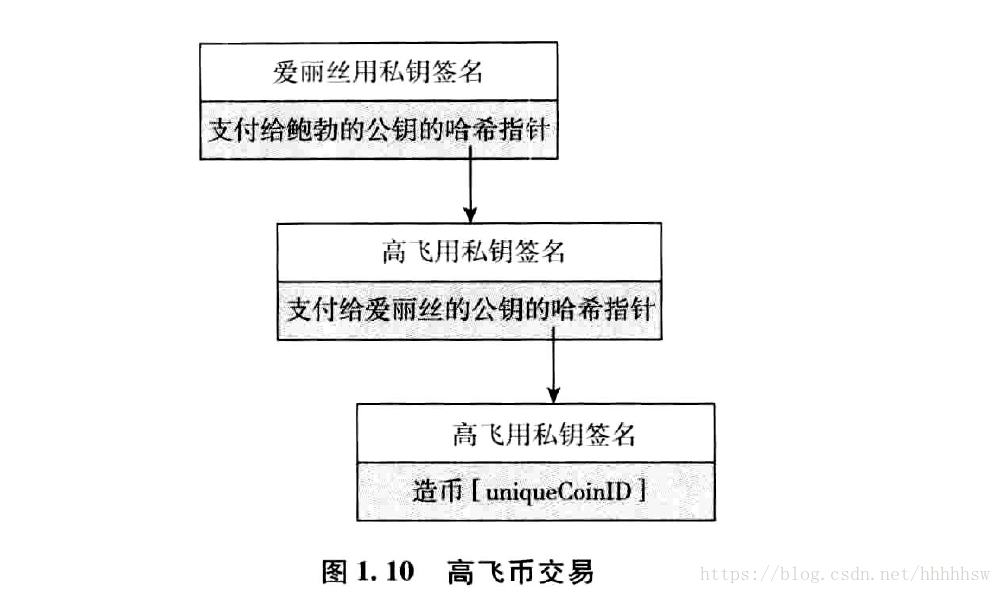
高飛造幣時用私鑰進行簽名,代表這個幣是有效幣。
高飛把此幣轉移給愛麗絲時,用私鑰簽署“將此幣轉移給愛麗絲”的宣告,這代表這個交易確實存在,愛麗絲擁有了這個幣。
愛麗絲可以將此幣轉移給鮑勃,所以她需要簽署一個“將此幣轉移給鮑勃”的宣告。鮑勃可以通過雜湊指標來追溯到這個幣是由高飛建立,並且驗證過程中的所有簽名來確定這個幣的有效性。
但這裡有一個致命的安全隱患:雙重支付。愛麗絲再將此幣轉移給鮑勃之後可以再將此幣轉移給查克,鮑勃和查克在追溯這個幣的有效性時,都是從上圖中支付給愛麗絲的公鑰的雜湊指標開始驗證的,所以他們兩都認為這個幣有效。
5. 財奴幣
一個叫財奴的指定實體將負責公佈包含所有發生過的交易歷史紀錄的僅增賬目,賬目的僅增特性保證了這個賬目的任何資料都會永久保留下來,不會被刪除。為執行這個僅增功能,財奴可以建立一個區塊鏈,並且財奴的數字簽名是針對最後一個雜湊指標。
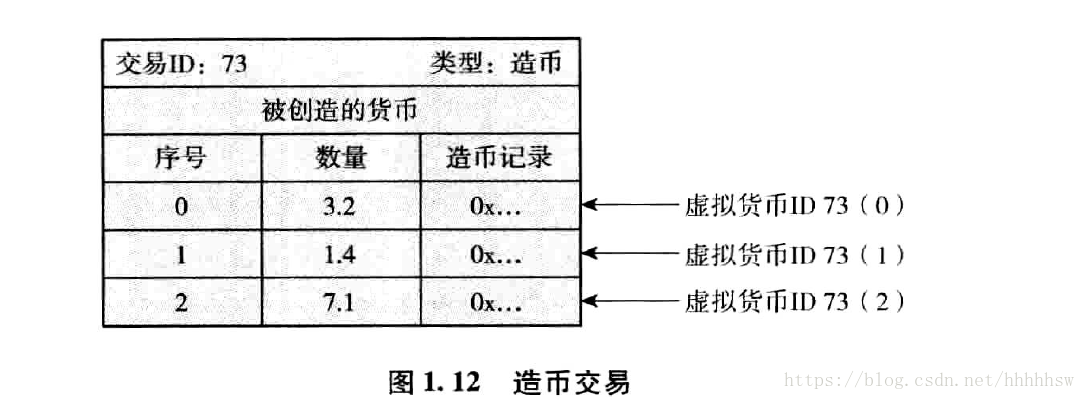
(1)造幣
不同於高飛幣,財奴幣可以在一次交易中建立多個幣量。
(2)付幣
只有當以下四個條件為真,付幣交易有效。
- 被消耗的幣為有效貨幣,即它們是在之前的交易建立的
- 被消耗的幣沒有在之前的某交易中被消耗掉。就是說,本次交易不是雙重支付
- 本次交易產生的幣值量等於消耗的幣值量,就是說只有財奴才可以建立新幣
- 本次交易被消耗的所有幣都有其所有者的有效簽署
在這個系統中,最大的問題就是中心化,財奴的權利過大。