本章是對前五章的總結

一、概述

Tensorflow框架的核心概念是計算圖：

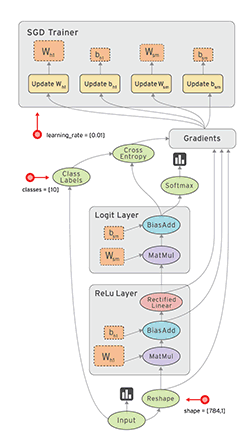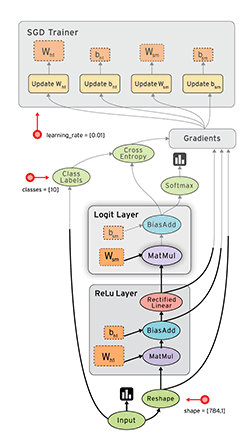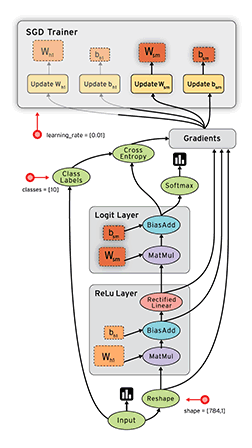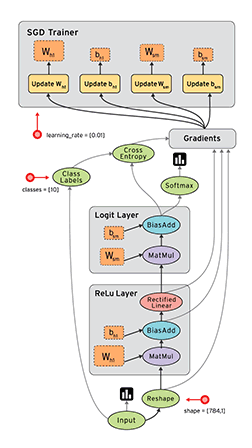
整個計算流圖的主要包含以下幾個部分：

• 匯入資料
• 網路結構
• 損失函式
• 反向傳播

由於Tensorflow框架的機制，反向傳播過程並不需要我們去描述。因此我們要做的就是：

• 定義網路的結構
• 定義損失函式與反向傳播演算法
• 訓練並測試模型

二、計算圖

import tensorflow as tf
import numpy as np

# 定義常量
a = tf.constant([1.0], name = 'a')
b = tf.constant([2.0], name = 'b')
result = a + b
print(result)
 

輸出結果：  

# 定義常量
a = tf.constant([1.0], name = 'a')
b = tf.constant([2.0], name = 'b')
result = a + b

# 定義會話
with tf.Session() as sess:
    print(sess.run(result))

輸出結果： 

上述的程式碼定義了一個計算圖，通過定義會話執行計算。可以形象地類比成一個管道系統，開始的時候我們只是構建了管道系統的結構與流通規則。但此時沒有水流入，通過定義會話，將水通入管道系統，最後才能出現結果。

其中的a，b，result在tensorflow中都別稱作張量（對運算結果的引用）

三、神經網路的搭建

在搭建神經網路之前，我們需要了解一下本次使用的資料集MNIST

MNSIT資料集是深度學習經典入門的demo，其訓練集包含了55000張圖片，驗證集包含了5000張圖片，測試集包含了10000張，其中每張圖片是以28*28*1的矩陣形式儲存

我們使用下面的程式碼來讀取資料

mnist = input_data.read_data_sets('./', one_hot = True)

這樣會在當前資料夾下出現4個檔案：

下面是一個簡單的神經網路模型

基於此建立一個簡單的神經網路：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np

# 使用下面語句在當前目錄下下載並讀取檔案，如果檔案已存在則直接讀取
mnist = input_data.read_data_sets('./', one_hot = True)

# 每個批次的大小
batch_size = 100

# 定義兩個placeholder,為資料的匯入預留兩個位置
# 這裡的 None表示第一個維度暫時未知,在實際執行的時候會給定
x = tf.placeholder(tf.float32, [None, 784])
y = tf.placeholder(tf.float32, [None, 10])

# 這裡的tf.matmul表示矩陣乘法
w1 = tf.Variable(tf.truncated_normal([784, 500], stddev = 0.1))
b1 = tf.Variable(tf.constant(0.1, shape = [500]))
a1 = tf.nn.relu(tf.matmul(x, w1) + b1)

w2 = tf.Variable(tf.truncated_normal([500,10], stddev = 0.1))
b2 = tf.Variable(tf.constant(0.1, shape = [10]))
logit = tf.nn.softmax(tf.matmul(a1, w2) + b2)

# 定義softmax損失函式
loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
    logits = logit, labels = tf.argmax(y, 1)))

# 使用梯度下降法
train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)

# 初始化變數
init = tf.global_variables_initializer()

# 將結果放在一個bool型別的列表中
# tf.argmax(y, 1) 表示按axis = 1,也就是按第二個維度取值最大的位置
correction_prediction = tf.equal(tf.argmax(y,1), tf.argmax(logit, 1))
# 求準確率
accuracy = tf.reduce_mean(tf.cast(correction_prediction, tf.float32))

# 定義會話
with tf.Session() as sess:
    sess.run(init)
    for i in range(20001):
        # 以100個樣本作為一個批次
        start = (i * batch_size) % mnist.train.num_examples
        end = min(start + batch_size, mnist.train.num_examples)
        
        # 把當前批次的資料匯入進神經網路
        sess.run(train_step,feed_dict = {x:mnist.train.images[start:end], y:mnist.train.labels[start:end]})
        if i % 1000 == 0:
            
            # 將訓練集和測試集匯入神經網路,計算準確率
            train_prediction = sess.run(accuracy, feed_dict = {x:mnist.train.images, y:mnist.train.labels})
            test_prediction = sess.run(accuracy, feed_dict = {x:mnist.test.images, y:mnist.test.labels})
            print("After %d, train correction: %g, test correction: %g" %(i, train_prediction, test_prediction))

執行結果：

四、優化演算法

通過簡單的搭建一個神經網路，我們可以瞭解到整個程式的大概面貌，但在實際使用情況中，需要對神經網路進行一些優化，以達到更好的預期效果。這裡我們加入了正則化和學習率衰減優化演算法。同時上面提到的程式碼從某種程度上來說，並不規範，因此新增優化演算法後並進行規範化後的程式碼如下：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

input_node = 784 # mnist資料集共有28*28個畫素，所以輸入節點共有784
output_node = 10 # 輸出層節點數
layer1_node = 500 # 隱藏層節點數
batch_size = 100 # 一個訓練batch中的訓練資料個數
learning_rate_base = 0.8 # 基礎學習率
learning_rate_decay = 0.99 # 學習率衰減率
regularization_rate = 0.0001 # 正則化項
training_steps = 30000 # 訓練輪數

def get_weight(shape, regularizer):
    '''
    如果有正則化項，則將weight加入到losses集合中
    '''
    weight = tf.get_variable('weight', shape, initializer = tf.truncated_normal_initializer(stddev = 0.1))
    if regularizer != None:
        tf.add_to_collection('losses', regularizer(weight))
    return weight

def get_bias(shape):
    bias = tf.get_variable('bias', shape, initializer = tf.constant_initializer(0.1))
    return bias

def inference(input_tensor, regularizer):
    '''
    神經網路正向傳播過程
    '''
    # 對神經網路的第一層賦予名稱layer1的名稱空間
    with tf.variable_scope('layer1'):
        weight = get_weight([input_node, layer1_node], regularizer)
        tf.summary.histogram('weight1', weight)
        bias = get_bias([layer1_node])
        layer1 = tf.nn.relu(tf.matmul(input_tensor, weight) + bias)
        
    # 對神經網路的輸出層賦予名稱layer2的名稱空間 
    with tf.variable_scope('layer2'):
        weight = get_weight([layer1_node, output_node], regularizer)
        tf.summary.histogram('weight2', weight)
        bias = get_bias([output_node])
        layer2 = tf.nn.softmax(tf.matmul(layer1, weight) + bias)
    return layer2


def train(mnist):
    # 定義輸入空白位
    x = tf.placeholder(tf.float32, [None, input_node], name = 'x-input')
    y = tf.placeholder(tf.float32, [None, output_node], name = 'y-input')
    
    # 定義L2正則化項
    regularizer = tf.contrib.layers.l2_regularizer(regularization_rate)
    
    # 計算神經網路前向傳播的結果
    logit = inference(x, regularizer)
    
    # 這裡與之前說到滑動平均模型裡的num_updates變數一致，通過模仿迭代次數來控制衰減速率
    global_step = tf.Variable(0, trainable = False)
    
    # 定義損失函式
    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
    logits = logit, labels = tf.argmax(y, 1))
    
    cross_entropy_mean = tf.reduce_mean(cross_entropy)
    
    # 總的損失等於交叉熵的損失和正則化損失的和
    loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
    
    # 學習率衰減函式
    learning_rate = tf.train.exponential_decay(
    learning_rate_base, # 基礎學習率，在此基礎上進行衰減
    global_step,        # 當前迭代的輪數
    mnist.train.num_examples, # 走完所有資料需要的迭代次數
    learning_rate_decay) # 學習率衰減速率
    
    # 使用梯度下降法優化
    train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step = global_step)
    
    # 測試輸出結果是否與真實標籤相等
    correction_prediction = tf.equal(tf.argmax(logit, 1), tf.argmax(y, 1))
    
    # 測試一組資料正確率
    # 這裡將correction_pred型別改為tf.float32
    accuracy = tf.reduce_mean(tf.cast(correction_prediction, tf.float32))

    # 引數初始化
    init = tf.global_variables_initializer()
    
    with tf.Session() as sess:    
        sess.run(init)
        
        # 開始訓練
        for i in range(training_steps):
            # 產生當前輪的訓練批次
            xs, ys = mnist.train.next_batch(batch_size)
            sess.run(train_step, feed_dict = {x: xs, y:ys})
            
            # 每一千次訓練測試一下驗證集正確率
            if i % 1000 == 0:
                train_acc = sess.run(accuracy, feed_dict = {x: mnist.train.images, y: mnist.train.labels})
                
                test_acc= sess.run(accuracy, feed_dict = {x: mnist.test.images, y: mnist.test.labels})
                print("After %d training step, train accuracy is %g, test accuracy is %g" %(i, train_acc, test_acc))

# 執行程式
mnist = input_data.read_data_sets('./', one_hot = True)
tf.reset_default_graph()
train(mnist)

 在tensorboard下，執行結果曲線圖，這裡的加粗線表示訓練集精度，另外的線表示測試集精度。當迭代到一定程度時，曲線收斂。

五、卷積神經網路

對於簡單的卷積神經網路，其結構如下圖所示：

有了之前的基礎，我們可以瞭解卷積神經網路的搭建。首先一般的卷積網路主要有：

• 卷積層
• 池化層
• 全連線層

其中全連線層與我們之前介紹的網路一樣

首先是卷積層：這裡的第一個和第二個維度表示了過濾器的尺寸，第三個維度表示了當前輸入圖層也就是上層的輸出的通道數，第四個維度表示了過濾器的個數。

回顧一下卷積層的操作：

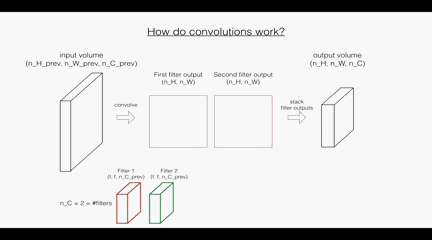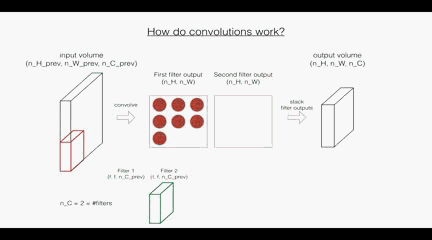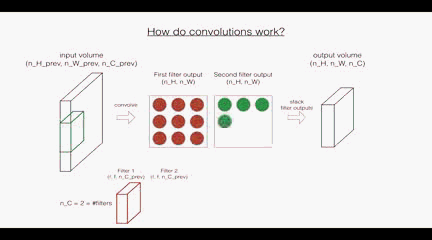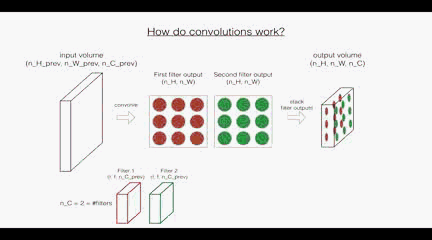
根據上面的圖示看， 

# 定義過濾器的權重
filter_weight = tf.get_variable('weight', [5,5,3,16], initializer = tf.truncated_normal_initializer(stddev = 0.1))

# 定義過濾器的偏置
bias = tf.get_variable('biases', [16], initializer = tf.truncated_normal_initializer(0.1))

之後我們定義卷積層運算：

conv = tf.nn.conv2d(input, filter_weight, strides = [1,1,1,1], padding = 'SAME')

這裡的步長由於支隊矩陣的長和寬有效，因此第一維和最後一維的一定為1

padding = 'SAME'表示用0填充，padding = 'VALID'表示不填充

設原影象尺寸為W * W，步長為s，過濾器尺寸為f * f，則經過卷積運算後的影象尺寸：

VALID：

SAME：

池化層又分成最大池化層和平均池化層：

# 最大池化層
# ksize維度裡第一個和第四個必須為1，第二個和第三個維度表示過濾器尺寸
pool = tf.nn.max_pool(actived_conv, ksize = [1,3,3,1],
                      strides = [1,2,2,1], padding = 'SAME')
# 平均池化層
pool = tf.nn.avg_pool(actived_conv, ksize = [1,3,3,1],
                      strides = [1,2,2,1], padding = 'SAME')

下面使用cifar-10資料集，cifar-10資料集總共有60000張彩色影象，50000張用於訓練，另外10000張用於測試。其中每張影象是32*32*3規格的。共有10個類別，每個類別有5000張

使用VGGNet網路將會帶來較好的效率，但也會因此產生巨大的時間開銷，因此這裡我們使用一個簡化版的VGG-16網路對影象進行識別：

import tensorflow as tf
import numpy as np
import pickle

# 讀取cifar-10資料集
def load_CIFAR_batch(filename):
    with open(filename, 'rb') as f:
        datadict = pickle.load(f,encoding='latin1')
        X = datadict['data']
        Y = datadict['labels']
        X = X.reshape(10000, 3, 32,32).transpose(0,2,3,1).astype("float")
        Y = np.array(Y)
        return X, Y

# 給定檔案路徑，解析資料為標準格式
def load_data(file_path):
    X_train = []
    Y_train = []
    file_name = file_path + "data_batch_"
    for i in range(1, 6):
        X, Y = load_CIFAR_batch(file_name + str(i))
        X_train.append(X)
        Y_train.append(Y)
    X_train = np.concatenate(X_train)
    Y_train = np.concatenate(Y_train)
    del X, Y
    
    X_test, Y_test = load_CIFAR_batch(file_path + "test_batch")
    
    train_label = np.zeros([Y_train.shape[0], 10])
    test_label = np.zeros([Y_test.shape[0], 10])
    for i in range(Y_train.shape[0]):
        train_label[i, Y_train[i]] = 1
    for i in range(Y_test.shape[0]):
        test_label[i, Y_test[i]] = 1
    
    return X_train, train_label, X_test, test_label

# 定義全連線層
def fc_op(input_op, name, n_out):
    n_in = input_op.get_shape()[-1].value
    
    with tf.name_scope(name) as scope:
        weight = tf.get_variable(
            name = scope + "w",
            shape = [n_in, n_out],
            initializer = tf.truncated_normal_initializer(stddev = 0.2))
        bias = tf.get_variable('bias',
                               [n_out],
                               initializer =  tf.constant_initializer(0.1))
        result = tf.matmul(input_op, weight) + bias
        
        return result

# 定義卷積層
def conv_op(input_op, name, kh, kw, n_out, dh, dw):
    '''
    input_op：上層輸入
    name：空間命名名稱
    kh,kw：過濾器的尺寸
    n_out：過濾器數目，也可以理解成輸出通道數
    dh,dw：步長的高，和寬
    '''
    
    # 獲取上層輸入的通道數目
    n_in = input_op.get_shape()[-1].value
    
    with tf.name_scope(name) as scope:
        # 定義過濾器
        kernel = tf.get_variable(
            name = scope + "w",
            shape = [kh, kw, n_in, n_out],
            initializer = tf.truncated_normal_initializer(stddev = 0.2))
        
        # 卷積運算
        conv = tf.nn.conv2d(input_op, kernel, (1, dh, dw, 1), padding = 'SAME')
        # 定義偏置
        bias = tf.get_variable(scope + "b", [n_out],  initializer = tf.constant_initializer(0.1))
        # relu啟用
        conv = tf.nn.relu(tf.nn.bias_add(conv, bias), name = scope)
        
        return conv

# 定義最大池化層
def pool_op(input_op, name ,kh, kw, dh, dw):
    '''
    input_op:上層輸入
    kh,kw：過濾器尺寸
    dh,dw：步長的高和寬
    '''
    pool = tf.nn.max_pool(input_op,
                          ksize = [1,kh,kw,1],
                          strides = [1,dh,dw,1],
                          padding = 'SAME',
                          name = name)
    return pool

# 定義神經網路的正向傳播
def inference(input_op, keep_prob):
    # 第一個卷積層
    conv1_1 = conv_op(input_op, name = 'conv1_1', kh = 3, kw = 3, n_out = 64,
                     dh = 1, dw = 1)
    conv1_2 = conv_op(conv1_1, name = 'conv1_2', kh = 3, kw = 3, n_out = 64,
                     dh = 1, dw = 1)
    pool_1 = pool_op(conv1_2, name = 'pool_1', kh = 2, kw =  2, dw = 2, dh = 2)
    
    
    # 第二個卷積層
    conv2_1 = conv_op(pool_1, name = 'conv2_1', kh = 3, kw = 3, n_out = 128,
                     dh = 1, dw = 1)
    conv2_2 = conv_op(conv2_1, name = 'conv2_2', kh = 3, kw = 3, n_out = 128,
                     dh = 1, dw = 1)
    pool_2 = pool_op(conv1_2, name = 'pool_2', kh = 2, kw =  2, dw = 2, dh = 2)
    
    
    # 第三個卷積層
    conv3_1 = conv_op(pool_2, name = 'conv3_1', kh = 3, kw = 3, n_out = 256,
                     dh = 1, dw = 1)
    conv3_2 = conv_op(conv2_1, name = 'conv3_2', kh = 3, kw = 3, n_out = 256,
                     dh = 1, dw = 1)
    pool_3 = pool_op(conv3_2, name = 'pool_3', kh = 2, kw =  2, dw = 2, dh = 2)
    

    # 將卷積層傳來的輸入壓成一個向量
    shape = pool_3.get_shape()
    flattened_shape = shape[1].value * shape[2].value * shape[3].value
    reshape = tf.reshape(pool_3, [-1, flattened_shape], name = 'reshape')
    
    # 使用dropout正則化，以keep_prob概率選擇神經元
    reshape = tf.nn.dropout(reshape, keep_prob)
    
    # 全連線層
    logit = fc_op(reshape, 'fc1', 10)
    
    return logit

def train(X_train, Y_train, X_test, Y_test):
    x = tf.placeholder(tf.float32, [None, 32, 32, 3])
    y = tf.placeholder(tf.float32, [None, 10])
    keep_prob = tf.placeholder(tf.float32)
    
    # 定義正向傳播
    logit = inference(x, keep_prob)
    
    # 定義損失函式
    loss = tf.reduce_mean(tf.nn.sparse_softmax_cross_entropy_with_logits(
        logits = logit, labels = tf.argmax(y, 1)))
    
    # 使用Adam下降法
    train_step = tf.train.AdamOptimizer(1e-4).minimize(loss)
    
    # 計算準確率
    correction_prediction = tf.equal(tf.argmax(logit, 1), tf.argmax(y, 1))
    accuracy = tf.reduce_mean(tf.cast(correction_prediction, tf.float32))
    
    # 初始化變數
    init = tf.global_variables_initializer()
    
    # 定義會話，開始訓練神經網路
    with tf.Session() as sess:
        sess.run(init)
        
        for i in range(30000):
            start = (i * batch_size) % X_train.shape[0]
            end = min(start + batch_size, X_train.shape[0])
            sess.run(train_step, feed_dict = {x:X_train[start:end], y:Y_train[start:end], keep_prob:0.9})
        # 總共迭代3萬次，如果將所有的資料集合直接傳入神經網路將會導致記憶體空間不足，一般的情況下我們可以選取批次逐次訓
        #練，最終將結果累加求平均。這裡為簡單起見，我僅僅從測試集中抽取了一個batch_size的結果測試模型效果
        if i % 1000 == 0:
            num_epoch_train = X_train.shape[0] // batch_size
            num_epoch_test = X_test.shape[0] // batch_size
            train_accuracy = 0
            test_accuracy = 0
            for j in range(num_epoch_train):
                start = (j * batch_size) % X_train.shape[0]
                end = min(start + batch_size, X_train.shape[0])
                train_accuracy += sess.run(accuracy, feed_dict = {x: X_train[start:end], y:Y_train[start:end],keep_prob:1.0})
            train_accuracy /= num_epoch_train
            for k in range(num_epoch_test):
                start = (k * batch_size) % X_test.shape[0]
                end = min(start + batch_size, X_test.shape[0])
                test_accuracy += sess.run(accuracy, feed_dict = {x: X_test[start:end], y:Y_test[start:end], keep_prob:1.0})
            test_accuracy /= num_epoch_test
            print("After %d, train correction: %g, test correction: %g" %(i, train_accuracy, test_accuracy))


            
# 執行訓練過程
batch_size = 128
X_train, Y_train, X_test, Y_test = load_data("C:/Users/14981/Desktop/dataset/cifar-10-batches-py/")
tf.reset_default_graph()
train(X_train, Y_train, X_test, Y_test)

這個網路由於結構比較簡單，因此識別效率大概在70左右。如果要提高整個訓練準確率，可以考慮使用其他的網路結構