演算法:稀疏矩陣之三元組表示
阿新 • • 發佈:2018-12-14
三元組的表示
(1)、目的:對於在實際問題中出現的大型的稀疏矩陣,若用常規分配方法在計算機中儲存,將會產生大量的記憶體浪費,而且在訪問和操作的時候也會造成大量時間上的浪費,為了解決這一問題,從而善生了多種解決方案。
(2)、由於其自身的稀疏特性,通過壓縮可以大大節省稀疏矩陣的記憶體代價。具體操作是:將非零元素所在的行、列以及它的值構成一個三元組(i,j,v),然後再按某種規律儲存這些三元組,這種方法可以節約儲存空間。
具體如下圖:

#define SMAX 1000 typedef struct { int i,j; //儲存非零元素的行和列資訊 datatype v; //非零元素的值 }SPNode; //定義三元組型別 typedef struct { int mu,nu,tu; //矩陣的行、列和非零元素的個數 SPNode data[SMAX]; //三元組表 }SPMatrix;
稀疏矩陣的轉置
操作:一個n*m的稀疏矩陣轉置後得到的將是一個m*n的矩陣。簡單來說就是講三元組中的行標和列標交換,但是僅僅是這樣就結束了麼? 當然不是。前面規定三元組的是按一行一行且每行中的元素是按列號從小到大的規律順序存放的,因此B 也必須按此規律實現。
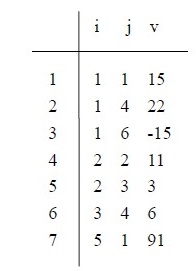 =》
=》 
演算法思路:
①A 的行、列轉化成B 的列、行; ②在A.data 中依次找第一列的、第二列的、直到最後一列,並將找到的每個三元組的行、列交換後順序儲存到B.data 中即可。
由於對於A的轉置是自上而下的,也就要求對於A中任意元素的轉置後位置必須是可知的,而原儲存順序是按行號排列的,所以轉置前同列的在前面的轉置後一定還在同行的前方。故確定了轉置後的每行的第一個元素的位置即確定整個順序。具體計算如下圖

程式碼如下:
void TransM1 (SPMatrix *A) { SPMatrix *B; int p,q,col; B=malloc(sizeof(SPMatrix)); /*申請儲存空間*/ B->mu=A->nu; B->nu=A->mu; B->tu=A->tu; /*稀疏矩陣的行、列、元素個數*/ if (B->tu != 0) /*有非零元素則轉換*/ { q=0; for (col=1; col<=(A->nu); col++) { /*按A 的列序轉換*/ for (p=1; p<= (A->tu); p++) /*掃描整個三元組表*/ if (A->data[p].j==col ) { B->data[q].i= A->data[p].j ; B->data[q].j= A->data[p].i ; B->data[q].v= A->data[p].v; q++; }/*if*/ } } /*if(B->tu>0)*/ return B; /*返回的是轉置矩陣的指標*/ } /*TransM1*/
