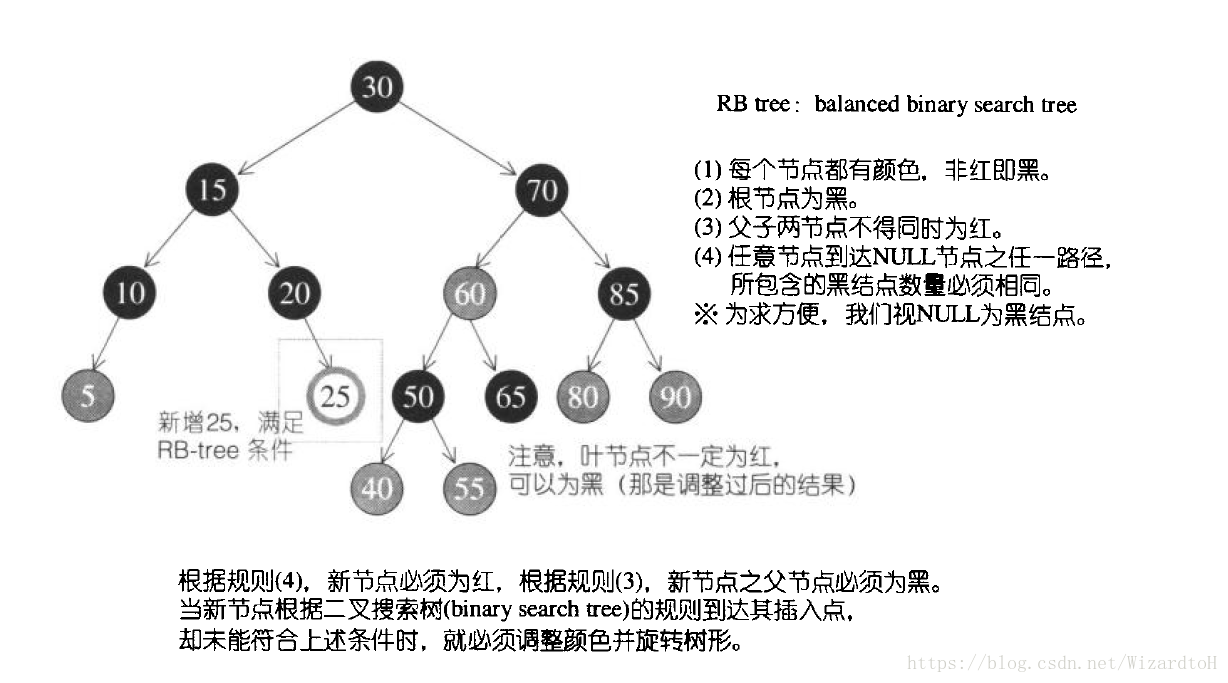
除了上一篇說到的AVL-tree之外，另一個常用的平衡二叉搜尋樹是RB-tree(紅黑樹)。RB-tree滿足二叉搜尋樹的規則之外，還遵循以下特性：

• 每個節點不是紅色就是黑色。
• 根節點為黑色。
• 如果節點為紅色，其子節點必須為黑色。
• 任意一個節點到到NULL（樹尾端）的任何路徑，所含之黑色節點數必須相同。

第四個特性和第三個特性確保了沒有一條路徑會比其他路徑長出倆倍。因而，紅黑樹是相對是接近平衡的二叉樹。和AVL樹相比，紅黑樹用非嚴格的平衡來換取增刪節點時候旋轉次數的降低，任何不平衡都會在三次旋轉之內解決；而AVL是嚴格平衡樹，因此在增加或者刪除節點的時候，，旋轉的次數可能會比紅黑樹要多，所以紅黑樹的插入/刪除效率更高

插入節點

根據紅黑樹的規則可以得出插入節點的要求：特性4限制了插入新節點必須是紅色節點；如果插入節點的父節點是紅色，那麼破壞了特性3。，那麼需要通過重新著色或旋轉，來維持性質； 如果插入節點的父節點是黑色，滿足規則。 按照以上的分析，可以得出4種插入的情況。

一、父節點為黑色，外側插入。

不存在伯父節點需要旋轉保持平衡。

二、父節點為黑色，內側插入。 不存在伯父節點需要旋轉保持平衡。

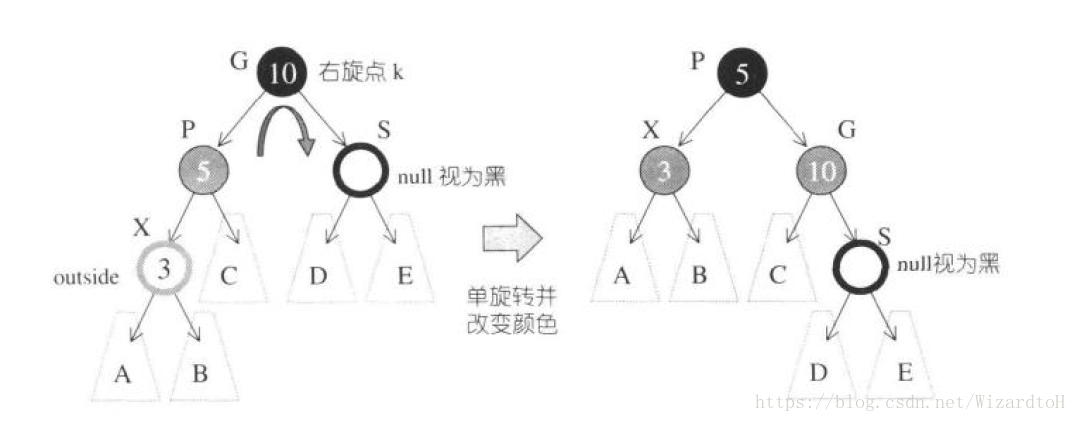
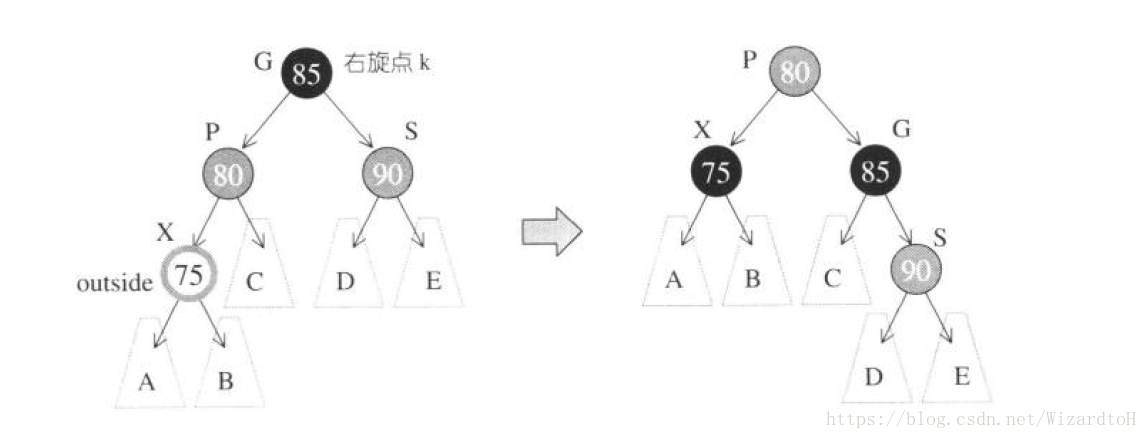
三、父節點為紅色，外側插入，祖父節點的父節點為黑色。

需要對父節點和祖父節點做一次單旋轉(SGI STL原始碼中並沒有進行旋轉，只改變了顏色，實際上改變顏色即可，因為有伯父節點時不存在不平衡)，同時進行一次顏色變換。如果此時祖父節點的父節點為黑色(特性3，紅色節點的子節點必須為黑色)，那麼插入完成，否則按照第四種情況進行處理。

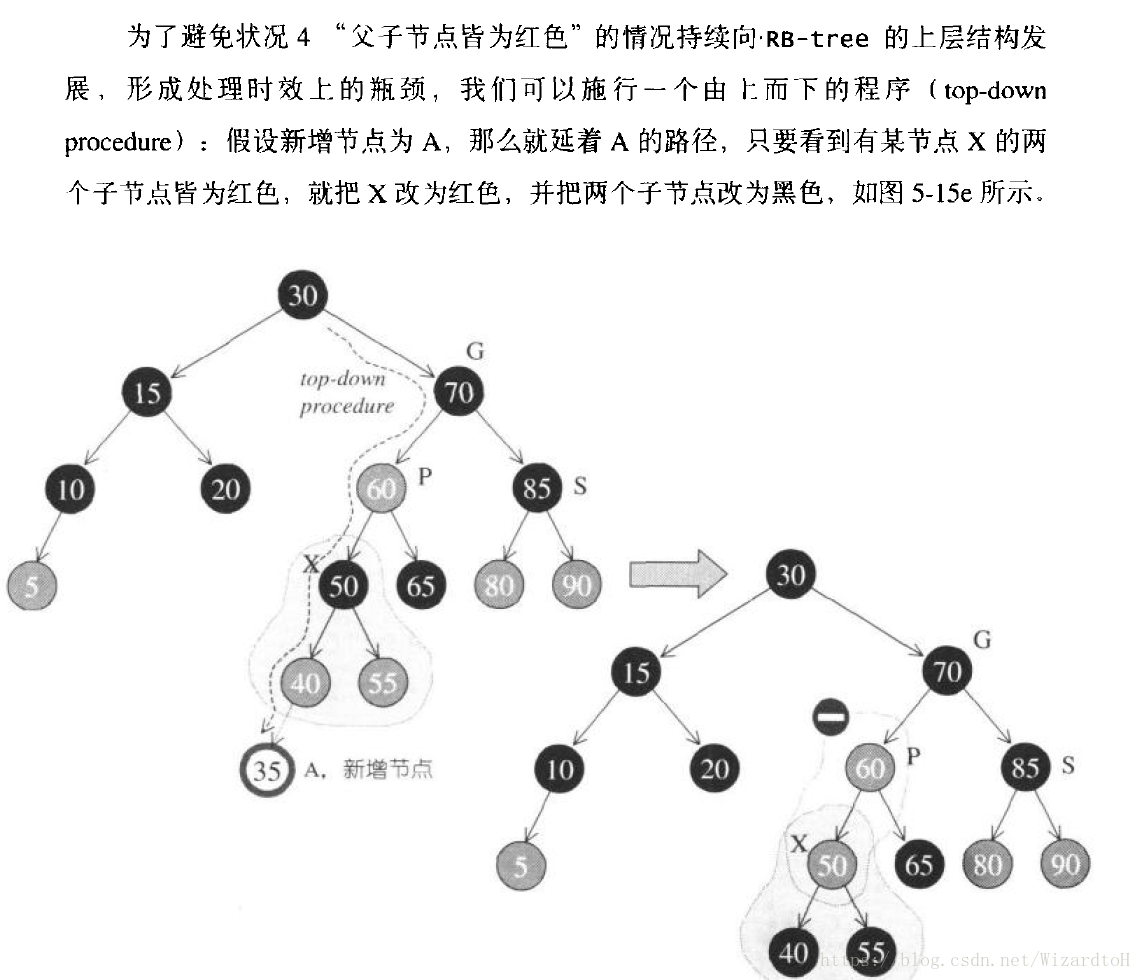
四、父節點為紅色，外側插入，祖父節點的父節點為紅色，需要從祖父節點開始繼續向上調整，直到調整過的祖父節點的父節點為黑色。

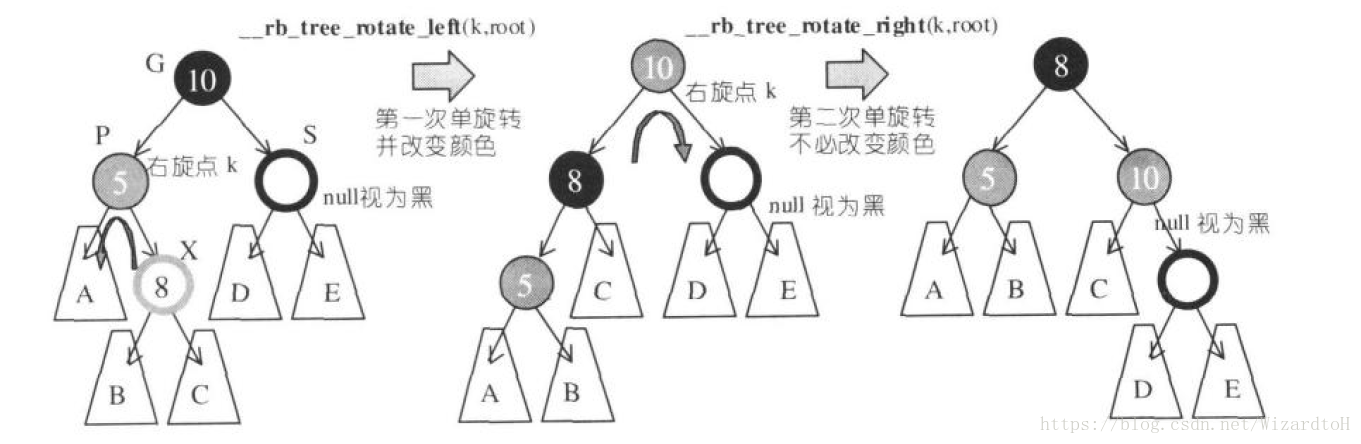
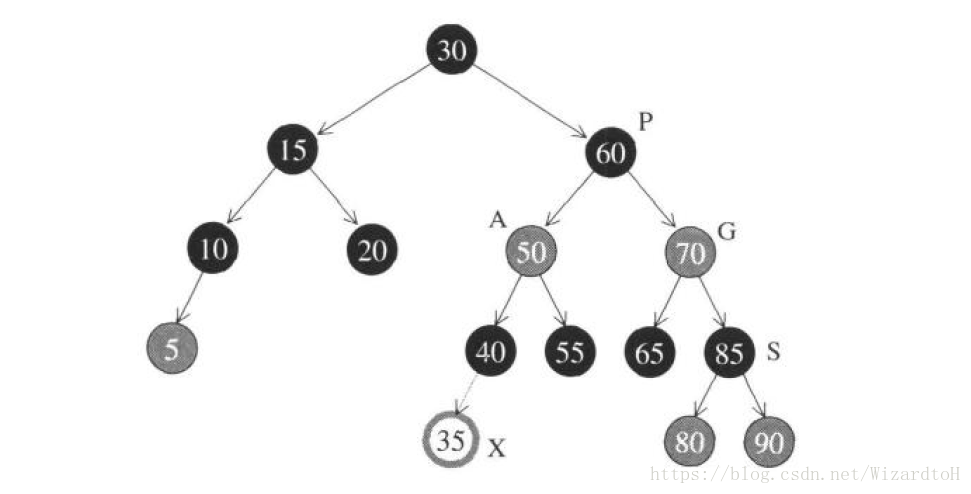
五、對第四種情況的優化(由原作者提供)

改變顏色後，如果X的父節點P也是紅色，那麼做一次單旋轉或者雙旋轉，同時改變顏色。在此之後，插入節點就很簡單了：直接插入，或者插入後做一次單旋轉。

RB-tree節點設計

SGI STL的樹節點，設計了兩層結構：__rb_tree_node_base為樹的基本成員，__rb_tree_node繼承了__rb_tree_node_base並提供節點的值。

typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false;
const __rb_tree_color_type __rb_tree_black = true;

struct __rb_tree_node_base
{
    typedef __rb_tree_color_type color_type;
    typedef __rb_tree_node_base* base_ptr;
    
    color_type color;
    base_ptr parent;
    base_ptr left;
    base_ptr right;
    
    // 最左邊為最小節點
    static base_ptr minimum(base_ptr x)
    {
        while (x->left != 0) x = x->left;
        return x;
    }
    
    // 最右邊為最大節點
    static base_ptr maximum(base_ptr x)
    {
        while (x->right != 0) x = x->right;
        return x;
    }
};

// 繼承了__rb_tree_node_base
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
  typedef __rb_tree_node<Value>* link_type;
  Value value_field;
};

RB-tree迭代器

迭代器同樣適用了雙層設計，節點和迭代器的雙層設計能夠保證在功能實現時的便捷。因為base層只包含了紅黑樹本身的抽象功能，繼承模板層才擁有其他功能的封裝，這樣一來針對紅黑樹本身的操作就不需要使用到上層的功能。

struct __rb_tree_base_iterator
{
    typedef __rb_tree_node_base::base_ptr base_ptr;
    typedef bidirectional_iterator_tag iterator_category;
    typedef ptrdiff_t difference_type;
    base_ptr node;    // 關聯到節點
    
    // 自增
    void increment()
    {
        if (node->right != 0) {   // 有右節點，一直向右節點的左子節點移動，直到最後得到自增結果
            node = node->right;
            while (node->left != 0)
                node = node->left;
        }
        else {    // 沒有右節點
            base_ptr y = node->parent;

			// 該節點是父節點的右子節點
			// 一直上溯右節點，直到node不是右子節點
            while (node == y->right) {
                node = y;
                y = y->parent;
            }
            
            // 上溯完成後，上溯後節點是父節點的左子節點，那麼父節點就是自增結果
            if (node->right != y)
                node = y;
                
           // 狀況4，當前迭代器為根節點，且無右節點時，根節點本身為自增結果(依賴於hrader節點的特殊實現)
        }
    }
    
    // 自減
    void decrement()
    {
        if (node->color == __rb_tree_red && node->parent->parent == node)
            // 狀況1，節點為紅色，且父節點的父節點為自己，自減結果為右子節點
            // 此情況發生於對end()迭代器自減，依賴於header節點的特殊實現，header節點的右子節點是整顆樹的最大節點
            node = node->right;
        else if (node->left != 0) {  // 有左子節點，找到左子樹中的最大值
            base_ptr y = node->left;
            while (y->right != 0)
                y = y->right;
            node = y;
        }
        else {   // 不是根節點，又沒有左子節點，一直上溯左節點，直到node不是左子節點，得到自減結果
            base_ptr y = node->parent;
            while (node == y->left) {
                node = y;
                y = y->parent;
            }
            node = y;
        }
    }
};

// 繼承了__rb_tree_base_iterator
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator
{
    typedef Value value_type;
    typedef Ref reference;
    typedef Ptr pointer;
    typedef __rb_tree_iterator<Value, Value&, Value*>             iterator;
    typedef __rb_tree_iterator<Value, const Value&, const Value*> const_iterator;
    typedef __rb_tree_iterator<Value, Ref, Ptr>                   self;
    typedef __rb_tree_node<Value>* link_type;
    
    __rb_tree_iterator() {}
    __rb_tree_iterator(link_type x) { node = x; }
    __rb_tree_iterator(const iterator& it) { node = it.node; }
    
    reference operator*() const { return link_type(node)->value_field; }
#ifndef __SGI_STL_NO_ARROW_OPERATOR
    pointer operator->() const { return &(operator*()); }
#endif /* __SGI_STL_NO_ARROW_OPERATOR */
    
    self& operator++() { increment(); return *this; }
    self operator++(int) {
        self tmp = *this;
        increment();
        return tmp;
    }
    
    self& operator--() { decrement(); return *this; }
    self operator--(int) {
        self tmp = *this;
        decrement();
        return tmp;
    }
};

RB-tree資料結構

以下為RB-tree的定義：

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree {
protected:
    typedef void* void_pointer;
    typedef __rb_tree_node_base* base_ptr;
    typedef __rb_tree_node<Value> rb_tree_node;
    typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;  // 專屬配置器，配置單位為一個節點的空間
    typedef __rb_tree_color_type color_type;
public:
    typedef Key key_type;
    typedef Value value_type;
    typedef value_type* pointer;
    typedef const value_type* const_pointer;
    typedef value_type& reference;
    typedef const value_type& const_reference;
    typedef rb_tree_node* link_type;
    typedef size_t size_type;
    typedef ptrdiff_t difference_type;
protected:
    link_type get_node() { return rb_tree_node_allocator::allocate(); }
    void put_node(link_type p) { rb_tree_node_allocator::deallocate(p); }

    // 配置空間並且構造
    link_type create_node(const value_type& x) {
        link_type tmp = get_node();
        __STL_TRY{
            construct(&tmp->value_field, x);
        }
        __STL_UNWIND(put_node(tmp));
        return tmp;
    }

    // 複製節點的值和顏色
    link_type clone_node(link_type x) {
        link_type tmp = create_node(x->value_field);
        tmp->color = x->color;
        tmp->left = 0;
        tmp->right = 0;
        return tmp;
    }

    void destroy_node(link_type p) {
        destroy(&p->value_field);
        put_node(p);
    }
public:
    // 迭代器定義
    typedef __rb_tree_iterator<value_type, reference, pointer> iterator;
    typedef __rb_tree_iterator<value_type, const_reference, const_pointer> const_iterator;
private:
    iterator __insert(base_ptr x, base_ptr y, const value_type& v);
    link_type __copy(link_type x, link_type p);
    void __erase(link_type x);

    // 初始化時，生成一個頭結點
    void init() {
        header = get_node();
        color(header) = __rb_tree_red;   // 頭結點顏色為紅色，區分於根節點
        root() = 0;
        leftmost() = header;
        rightmost() = header;
    }
...
}

RB-tree的構造與記憶體管理

RB-tree的記憶體管理使用專屬的配置器rb_tree_node_allocator，並提供兩種構造：

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc = alloc>
class rb_tree {
protected:
    typedef __rb_tree_node<Value> rb_tree_node;
    typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator;  // 專屬配置器，配置單位為一個節點的空間
public:
    // 預設構造，使用init函式生成一個帶header
    rb_tree(const Compare& comp = Compare())
        : node_count(0), key_compare(comp) {
        init();
    }

   // 拷貝另一個樹進行構造
    rb_tree(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x)
        : node_count(0), key_compare(x.key_compare)
    {
        header = get_node();
        color(header) = __rb_tree_red;
        if (x.root() == 0) {
            root() = 0;
            leftmost() = header;
            rightmost() = header;
        }
        else {
            __STL_TRY{
                root() = __copy(x.root(), header);
            }
            __STL_UNWIND(put_node(header));
            leftmost() = minimum(root());
            rightmost() = maximum(root());
        }
        node_count = x.node_count;
    }
    ~rb_tree() {
        clear();
        put_node(header);
    }
}
...

init會產生一個header節點，其父節點為根節點，左子節點為最小節點，右子節點為最大節點，每當插入新節點時需要維護header節點的正確性。

RB-tree的元素操作

一、元素插入insert_equal insert_equal允許插入鍵值一致的節點，返回值是指向新增節點的迭代器。

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_equal(const Value& v)
{
    link_type y = header;
    link_type x = root();

    // 比較key值大小，小向左，大向右
    while (x != 0) {
        y = x;
        x = key_compare(KeyOfValue()(v), key(x)) ? left(x) : right(x);
    }
    // x為新值插入點，y為父節點，v是插入值
    return __insert(x, y, v);
}

二、元素插入insert_unique insert_unique不允許插入鍵值重複的節點，返回值是pair值，包括是否插入成功以及插入成功後的新增節點迭代器。

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value& v)
{
    link_type y = header;
    link_type x = root();
    bool comp = true;
    // 比較key值大小，小向左，大向右
    while (x != 0) {
        y = x;
        comp = key_compare(KeyOfValue()(v), key(x));
        x = comp ? left(x) : right(x);
    }
    
    iterator j = iterator(y);   // 父節點迭代器
    if (comp)                     // comp為true，表示插入節點較小，插入左側
        if (j == begin())       // 如果父節點是最左節點，x為新值插入點，y為父節點，v是插入值
            return pair<iterator,bool>(__insert(x, y, v), true);
        else  // 如果父節點不是最左節點，將迭代器向前移動
            --j;
            
     // 比較向前移動後的節點和插入節點的鍵值大小，新值較大則插入右側
    if (key_compare(key(j.node), KeyOfValue()(v)))
        return pair<iterator,bool>(__insert(x, y, v), true);
        
    //  否則，不大不小就是重複，那麼返回重複的節點並告知失敗
    return pair<iterator,bool>(j, false);
}

三、插入操作__insert 以下為真正的執行插入節點操作。

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::
__insert(base_ptr x_, base_ptr y_, const Value& v) {
    link_type x = (link_type) x_;
    link_type y = (link_type) y_;
    link_type z;
    
    // 當插入節點為頭結點或插入鍵值小於父節點時
    // x!=0，插入點不為NULL為特殊情況在insert_unique的另一個版本中使用
    if (y == header || x != 0 || key_compare(KeyOfValue()(v), key(y))) {
        z = create_node(v);
        left(y) = z;        // 插入父節點的左側，當父節點為header時等價於leftmost() = z; 
        if (y == header) {
            root() = z;
            rightmost() = z;
        }
        else if (y == leftmost())
            leftmost() = z;           // 父節點為最小值，直接插入左側
    }
    else {  // 插入鍵值大於父節點的情況
        z = create_node(v);
        right(y) = z;
        if (y == rightmost())
            rightmost() = z;            // 父節點為最大值，直接插入右側
    }

    // 為插入節點設定父節點等
    parent(z) = y;
    left(z) = 0;
    right(z) = 0;

	// 進行平衡(改變顏色，進行旋轉)
    __rb_tree_rebalance(z, header->parent);
    ++node_count;
    return iterator(z);
}

三、調整樹 __rb_tree_rebalance

inline void
__rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
    // 因為規則：任意一個節點到到NULL（樹尾端）的任何路徑，所含之黑色節點數必須相同
    // 所以插入節點預設為紅色，保證這條規則必然符合
    x->color = __rb_tree_red;  

    // 父節點顏色為紅，且當前節點不為根節點(違反規則：如果節點為紅色，其子節點必須為黑色)
    while (x != root && x->parent->color == __rb_tree_red) {
        if (x->parent == x->parent->parent->left) {
            // 父節點是祖父節點的左子節點
            __rb_tree_node_base* y = x->parent->parent->right;
            if (y && y->color == __rb_tree_red) {   
                // 伯父節點存在且為紅色(伯父節點必然和父節點同色)
                // 因為規則：如果節點為紅色，其子節點必須為黑色，插入點位紅色不符合要求
                // 所以此時需要改變父節點和伯父節點的顏色為黑，祖父節點為紅
                x->parent->color = __rb_tree_black;
                y->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                
                // 同時以祖父節點為調整起點繼續調整
                // 如果祖父節點的父節點為黑色按照迴圈條件就調整結束
                // 否則繼續調整
                x = x->parent->parent;
                // 注意：上文中介紹插入情況時，有伯父節點還需要進行一次旋轉，實際程式碼中並沒有
            }
            else {
                // 伯父節點不存在，需要進行旋轉保持平衡
                if (x == x->parent->right) {
                   // 插入節點為右節點，內側插入，需要先左旋再右旋
                   // 以父節點為旋轉點進行左旋
                    x = x->parent;
                    __rb_tree_rotate_left(x, root);
                }
                
                // 使父節點顏色為黑，祖父節點顏色為紅，這樣旋轉之後顏色和深度都能保證平衡
                x->parent->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                
               // 以祖父節點為旋轉點進行右旋
                __rb_tree_rotate_right(x->parent->parent, root);
            }
        }
        else {
           // 父節點是祖父節點的右節點，和以上的情況對稱
            __rb_tree_node_base* y = x->parent->parent->left;
            if (y && y->color == __rb_tree_red) {
                x->parent->color = __rb_tree_black;
                y->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                x = x->parent->parent;
            }
            else {
                if (x == x->parent->left) {
                    x = x->parent;
                    __rb_tree_rotate_right(x, root);
                }
                x->parent->color = __rb_tree_black;
                x->parent->parent->color = __rb_tree_red;
                __rb_tree_rotate_left(x->parent->parent, root);
            }
        }
    }

    // 按照規則根節點始終為黑
    root->color = __rb_tree_black;
}

// 左旋轉
inline void
__rb_tree_rotate_left(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
    __rb_tree_node_base* y = x->right;  // 旋轉點的右子節點
    // 1、將y的左子節點設定成x的右子節點
    x->right = y->left; 
    if (y->left != 0)
        y->left->parent = x;
    // 2、將y的父節點設定成x的父節點
    y->parent = x->parent;

    // 3、將y替換到x的位置
    if (x == root)
        root = y;
    else if (x == x->parent->left)
        x->parent->left = y;
    else
        x->parent->right = y;
  
    // 4、將x設定成y的左子節點
    y->left = x;
    x->parent = y;
}

// 右旋轉
inline void
__rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
    __rb_tree_node_base* y = x->left;  // 選裝點的左子節點
    // 1、將y的右子節點設定成x的左子節點
    x->left = y->right;
    if (y->right != 0)
        y->right->parent = x;
    // 2、將y的父節點設定成x的父節點
    y->parent = x->parent;

    // 3、將y替換到x的位置
    if (x == root)
        root = y;
    else if (x == x->parent->right)
        x->parent->right = y;
    else
        x->parent->left = y;

    // 4、將x設定成y的右子節點
    y->right = x;
    x->parent = y;
}

元素查詢

查詢函式提供兩個版本，其中一個返回const迭代器。

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::find(const Key& k) {
    link_type y = header; 
    link_type x = root(); 

    // 節點不為空
    while (x != 0)
        // 比較查詢值和當前值的大小，大向右，小或等於向左
        // y用來儲存x節點，最後返回結果，因為小於是向左移動，找到之後會一直向右直到葉子節點為空
        if (!key_compare(key(x), k))
            y = x, x = left(x);                    
        else
            x = right(x); 
            
    // 獲取查詢結果y的迭代器
    // 判斷y是否為end()也就是header節點，此時返回end()
    // 判斷k是否大於j的值，如果是說明沒有找到，返回end()
    iterator j = iterator(y);
    return (j == end() || key_compare(k, key(j.node))) ? end() : j;
}

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::const_iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::find(const Key& k) const {
    link_type y = header; 
    link_type x = root();

    while (x != 0) {
        if (!key_compare(key(x), k))
            y = x, x = left(x);
        else
            x = right(x);
    }
    const_iterator j = const_iterator(y);
    return (j == end() || key_compare(k, key(j.node))) ? end() : j;
}