我們都知道，計算機的起源是數學中的二進位制計數法。可以說，沒有二進位制，就沒有如今的計算機系統。那什麼是二進位制呢？為什麼計算機要使用二進位制，而不是我們日常生活中的十進位制呢？如何在程式碼中操作二進位制呢？專欄開始，我們就從計算機認知的起源——二進位制出發，講講它在計算機中的“玄機”。

什麼是二進位制計數法？
為了讓你更好地理解二進位制計數法，我們先來簡單地回顧一下人類計數的發展史。

原始時代，人類用路邊的小石子，來統計放牧歸來的羊只數量，這表明我們很早就產生了計數的意識。後來，羅馬人用手指作為計數的工具，並在羊皮上畫出Ⅰ、Ⅱ、Ⅲ來代替手指的數量。表示一隻手時，就寫成“Ⅴ”形，表示兩隻手時，就畫成“ⅤⅤ”形等等。

公元 3 世紀左右，印度數學家（也有說法是阿拉伯人）發明了阿拉伯數字。阿拉伯數字由從 0 到 9 這樣 10 個計數符號組成，並採取進位製法，高位在左，低位在右，從左往右書寫。由於阿拉伯數字本身筆畫簡單，演算便利，因此它們逐漸在各國流行起來，成為世界通用的數字。

日常生活中，我們廣泛使用的十進位制計數法，也是基於阿拉伯數字的。這也是十進位制計數法的基礎。因此，相對其他計數方法，十進位制最容易被我們所理解。

讓我們來觀察一個數字：2871。

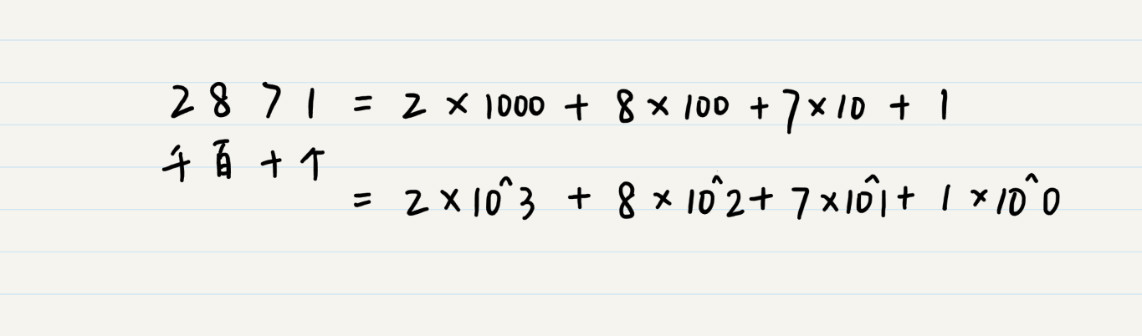
其中 ^ 表示冪或次方運算。十進位制的數位（千位、百位、十位等）全部都是 10^n 的形式。需要特別注意的是，任何非 0 數字的 0 次方均為 1。在這個新的表示式裡，10 被稱為十進位制計數法的基數，也是十進位制中“十”的由來。這個我想你應該好理解，因為這和我們日常生活的習慣是統一的。

明白了十進位制，我們再試著用類似的思路來理解二進位制的定義。我以二進位制數字 110101 為例，解釋給你聽。我們先來看，這裡 110101 究竟代表了十進位制中的數字幾呢？

剛才我們說了，十進位制計數是使用 10 作為基數，那麼二進位制就是使用 2 作為基數，類比過來，二進位制的數位就是 2^n 的形式。如果需要將這個數字轉化為人們易於理解的十進位制，我們就可以這樣來計算：

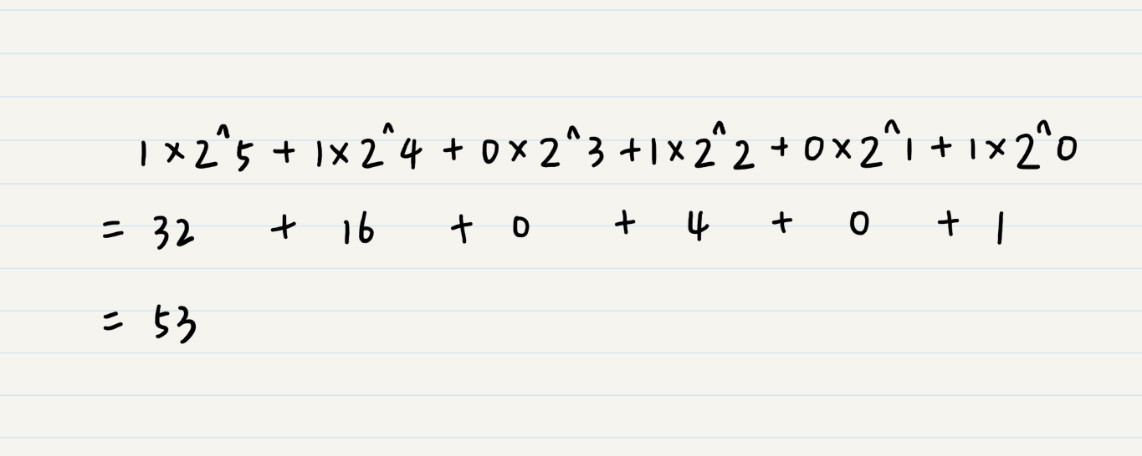
按照這個思路，我們還可以推匯出八進位制（以 8 為基數）、十六進位制（以 16 為基數）等等計數法，很簡單，我在這裡就不贅述了。

至此，你應該已經理解了什麼是二進位制。但是僅有數學的理論知識是不夠的，結合相關的程式碼實踐，相信你會有更深刻的印象。

基於此，我們來看看二進位制和十進位制數在 Java 語言中是如何互相轉換的，並驗證一下我們之前的推算。我這裡使用的是 Java 語言來實現的，其他主流的程式語言實現方式都是類似的。

這段程式碼的實現採用了 Java 的 BigInteger 類及其 API 函式，我都加了程式碼註釋，並且穿插一些解釋，你應該可以看懂。

首先，我們引入 BigInteger 包，通過它和 Integer 類的 API 函式進行二進位制和十進位制的互相轉換。

import java.math.BigInteger;

public class Lesson1_1 {

/**

* @Description: 十進位制轉換成二進位制
* @param decimalSource
* @return String
*/
public static String decimalToBinary(int decimalSource) {
BigInteger bi = new BigInteger(String.valueOf(decimalSource)); // 轉換成 BigInteger 型別，預設是十進位制
return bi.toString(2); // 引數 2 指定的是轉化成二進位制
}

/**
* @Description: 二進位制轉換成十進位制
* @param binarySource
* @return int
*/
public static int binaryToDecimal(String binarySource) {
BigInteger bi = new BigInteger(binarySource, 2); // 轉換為 BigInteger 型別，引數 2 指定的是二進位制
return Integer.parseInt(bi.toString()); // 預設轉換成十進位制
}
}

然後，我們通過一個十進位制數和一個二進位制數，來驗證一下上述程式碼的正確性。

public static void main(String[] args) {

int a = 53;
String b = "110101";
System.out.println(String.format(" 數字 %d 的二進位制是 %s", a, Lesson1_1.decimalToBinary(a))); // 獲取十進位制數 53 的二進位制數
System.out.println(String.format(" 數字 %s 的十進位制是 %d", b, Lesson1_1.binaryToDecimal(b))); // 獲取二進位制數 110101 的十進位制數

}

這段程式碼執行的結果是：十進位制數字 53 的二進位制是 110101，二進位制數字 110101 的十進位制是 53。

好了，關於十進位制和二進位制的概念以及進位制之間的相互轉換，你應該都很清楚了。既然有十進位制，又有二進位制，你可能就要問了，為啥計算機使用的是二進位制而不是十進位制呢？

計算機為什麼使用二進位制？
我覺得，計算機使用二進位制和現代計算機系統的硬體實現有關。組成計算機系統的邏輯電路通常只有兩個狀態，即開關的接通與斷開。

斷開的狀態我們用“0”來表示，接通的狀態用“1”來表示。由於每位資料只有斷開與接通兩種狀態，所以即便系統受到一定程度的干擾時，它仍然能夠可靠地分辨出數字是“0”還是“1”。因此，在具體的系統實現中，二進位制的資料表達具有抗干擾能力強、可靠性高的優點。

相比之下，如果用十進位制設計具有 10 種狀態的電路，情況就會非常複雜，判斷狀態的時候出錯的機率就會大大提高。

另外，二進位制也非常適合邏輯運算。邏輯運算中的“真”和“假”，正好與二進位制的“0”和“1”兩個數字相對應。邏輯運算中的加法（“或”運算）、乘法（“與”運算）以及否定（“非”運算）都可以通過“0”和“1”的加法、乘法和減法來實現。

二進位制的位操作
瞭解了現代計算機是基於二進位制的，我們就來看看，計算機語言中針對二進位制的位操作。這裡的位操作，也叫作位運算，就是直接對記憶體中的二進位制位進行操作。常見的二進位制位操作包括向左移位和向右移位的移位操作，以及“或”“與”“異或”的邏輯操作。下面我們一一來看。

向左移位
我們先來看向左移位。

二進位制 110101 向左移一位，就是在末尾新增一位 0，因此 110101 就變成了 1101010。請注意，這裡討論的是數字沒有溢位的情況。

所謂數字溢位，就是二進位制數的位數超過了系統所指定的位數。目前主流的系統都支援至少 32 位的整型數字，而 1101010 遠未超過 32 位，所以不會溢位。如果進行左移操作的二進位制已經超出了 32 位，左移後數字就會溢位，需要將溢位的位數去除。

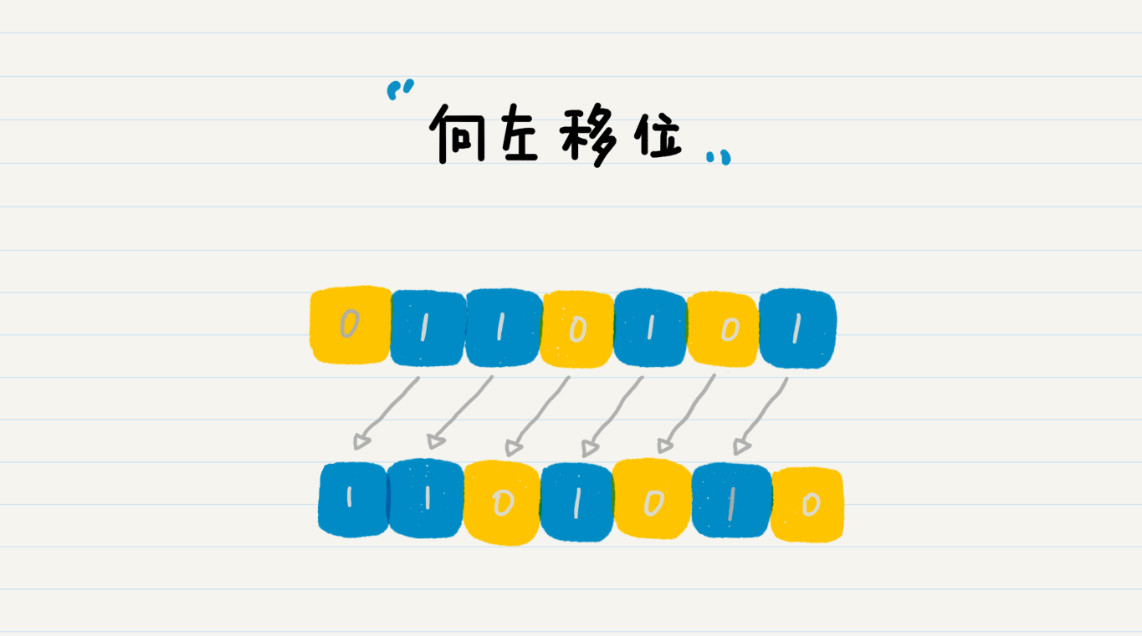
在這個例子中，如果將 1101010 換算為十進位制，就是 106，你有沒有發現，106 正好是 53 的 2 倍。所以，我們可以得出一個結論：二進位制左移一位，其實就是將數字翻倍。

向右移位
接下來我們來看向右移位。

二進位制 110101 向右移一位，就是去除末尾的那一位，因此 110101 就變成了 11010（最前面的 0 可以省略）。我們將 11010 換算為十進位制，就是 26，正好是 53 除以 2 的整數商。所以二進位制右移一位，就是將數字除以 2 並求整數商的操作。

下面我們來看看，用程式碼如何進行移位操作。

import java.math.BigInteger;

public class Lesson1_2 {

/**
* @Description: 向左移位
* @param num- 等待移位的十進位制數, m- 向左移的位數
* @return int- 移位後的十進位制數
*/
public static int leftShift(int num, int m) {
return num << m;
}

/**
* @Description: 向右移位
* @param num- 等待移位的十進位制數, m- 向右移的位數
* @return int- 移位後的十進位制數
*/
public static int rightShift(int num, int m) {
return num >>> m;
}

}

然後，我們用一段測試程式碼驗證下結果。

public static void main(String[] args) {

int num = 53;
int m = 1;
System.out.println(String.format(" 數字 %d 的二進位制向左移 %d 位是 %d", num, m, Lesson1_2.leftShift(num, m))); // 測試向左移位
System.out.println(String.format(" 數字 %d 的二進位制向右移 %d 位是 %d", num, m, Lesson1_2.rightShift(num, m))); // 測試向右移位

System.out.println();

m = 3;
System.out.println(String.format(" 數字 %d 的二進位制向左移 %d 位是 %d", num, m, Lesson1_2.leftShift(num, m))); // 測試向左移位
System.out.println(String.format(" 數字 %d 的二進位制向右移 %d 位是 %d", num, m, Lesson1_2.rightShift(num, m))); // 測試向右移位

}

這段程式碼的執行結果是：數字 53 向左移 1 位是 106；數字 53 向右移 1 位是 26。數字 53 向左移 3 位是 424，數字 53 向右移 3 位是 6。

我來解釋一下。其中，移位 1 次相當於乘以或除以 2，而移位 3 次就相當於乘以或除以 8（即 2 的 3 次方）。細心的話，你可能已經發現，Java 中的左移位和右移位的表示是不太一樣的。

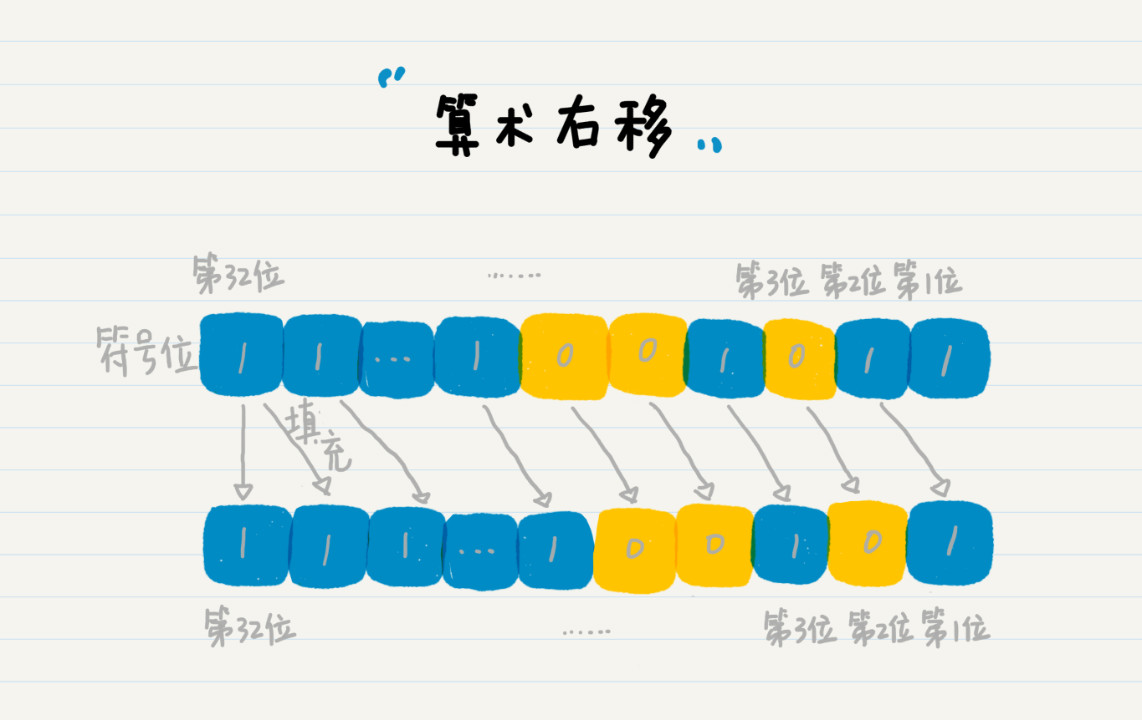
左移位是 <<，那右移位為什麼是 >>> 而不是 >> 呢？實際上，>> 也是右移操作。簡單來說，之所以有這兩種表達方式，根本原因是 Java 的二進位制數值中最高一位是符號位。這裡我給你詳細解釋一下。

當符號位為 0 時，表示該數值為正數；當符號位為 1 時，表示該數值為負數。我們以 32 位 Java 為例，數字 53 的二進位制為 110101，從右往左數的第 32 位是 0，表示該數是正數，只是通常我們都將其省略。

如果數字是 -53 呢？那麼第 32 位就不是 0，而是 1。請注意我這裡列出的是補碼。

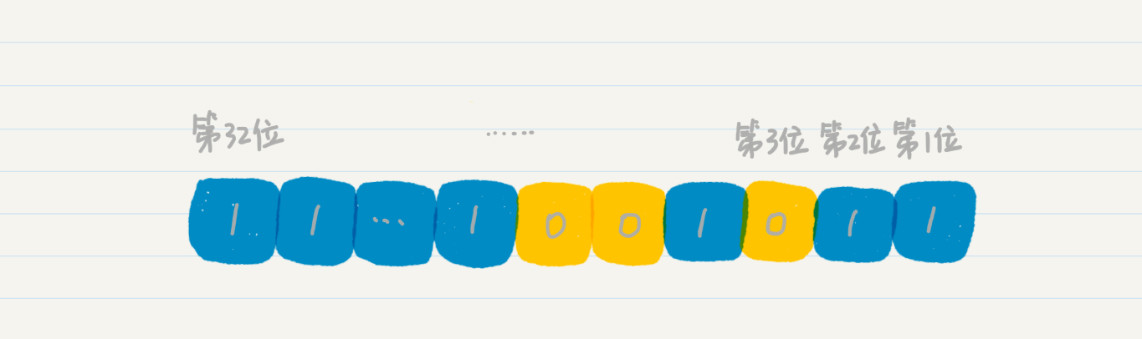
那麼這個時候向右移位，就會產生一個問題：對於符號位（特別是符號位為 1 的時候），我們是否也需要將其右移呢？因此，Java 裡定義了兩種右移，邏輯右移和算術右移。邏輯右移 1 位，左邊補 0 即可。

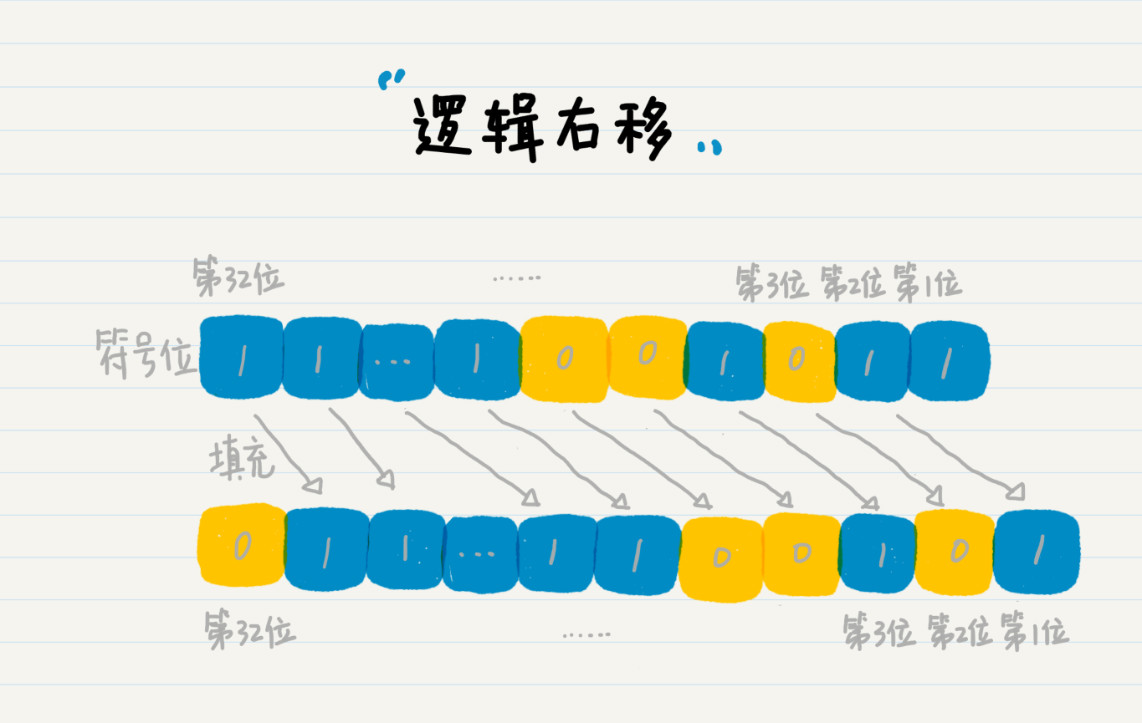
算術右移時保持符號位不變，除符號位之外的右移一位並補符號位 1。補的 1 仍然在符號位之後。

邏輯右移在 Java 和 Python 語言中使用 >>> 表示，而算術右移使用 >> 表示。如果你有興趣，可以自己編碼嘗試一下，看看這兩種操作符輸出的結果有何不同。

在 C 或 C++ 語言中，邏輯右移和算數右移共享同一個運算子 >>。那麼，編譯器是如何決定使用邏輯右移還是算數右移呢？答案是，取決於運算數的型別。如果運算數型別是 unsigned，則採用邏輯右移；而是 signed，則採用算數右移。如果你針對 unsigned 型別的資料使用算數右移，或者針對 signed 型別的資料使用邏輯右移，那麼你首先需要進行型別的轉換。

由於左移位無需考慮高位補 1 還是補 0（符號位可能為 1 或 0），所以不需要區分邏輯左移和算術左移。

位的“或”
我們剛才說了，二進位制的“1”和“0”分別對應邏輯中的“真”和“假”，因此可以針對位進行邏輯操作。

邏輯“或”的意思是，參與操作的位中只要有一個位是 1，那麼最終結果就是 1，也就是“真”。如果我們將二進位制 110101 和 100011 的每一位對齊，進行按位的“或”操作，就會得到 110111。

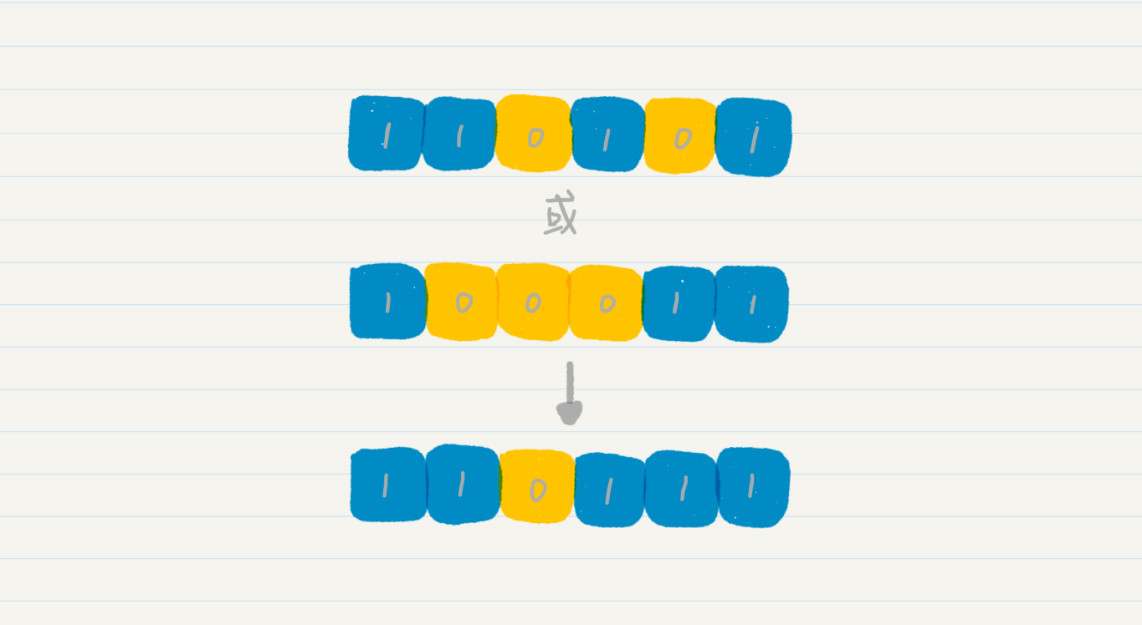
位的“與”
同理，我們也可以針對位進行邏輯“與”的操作。“與”的意思是，參與操作的位中必須全都是 1，那麼最終結果才是 1（真），否則就為 0（假）。如果我們將二進位制 110101 和 100011 的每一位對齊，進行按位的“與”操作，就會得到 100001。

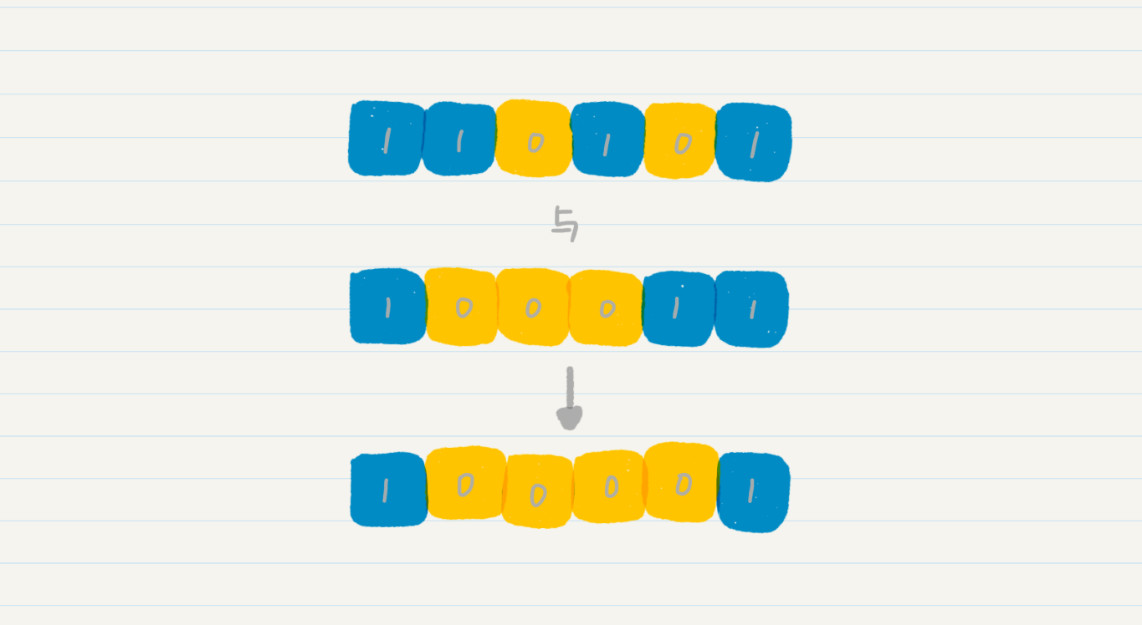
位的“異或”
邏輯“異或”和“或”有所不同，它具有排異性，也就是說如果參與操作的位相同，那麼最終結果就為 0（假），否則為 1（真）。所以，如果要得到 1，參與操作的兩個位必須不同，這就是此處“異”的含義。我們將二進位制 110101 和 100011 的每一位對齊，進行按位的“異或”操作，可以得到結果是 10110。

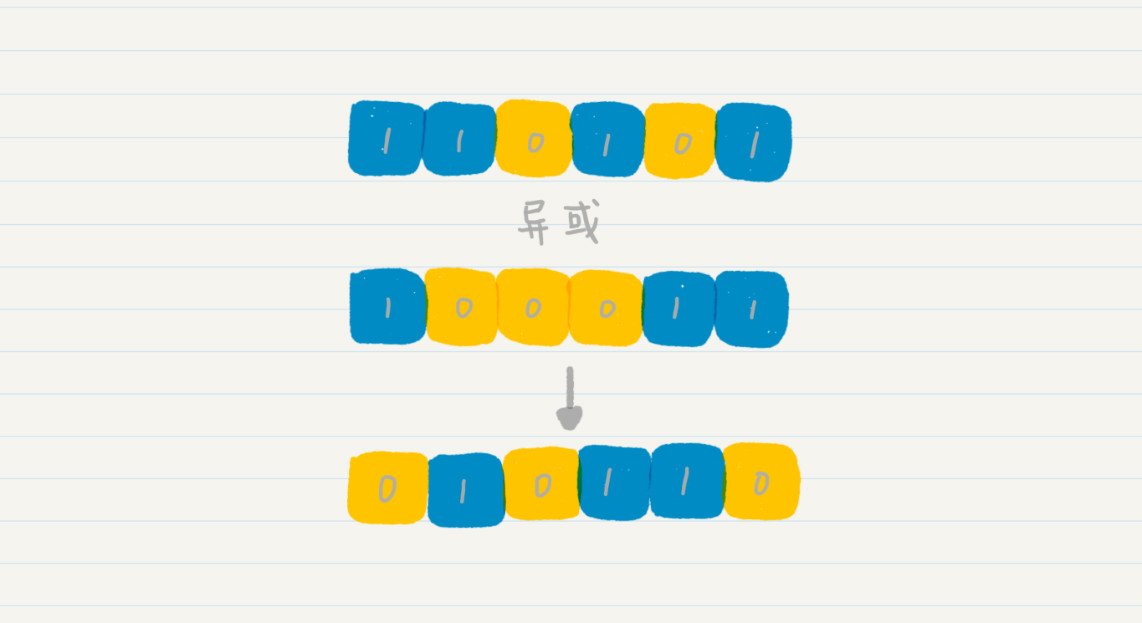
我總結一下，“異或”操作的本質其實就是，所有數值和自身進行按位的“異或”操作之後都為 0。而且要通過“異或”操作得到 0，也必須通過兩個相同的數值進行按位“異或”。這表明了兩個數值按位“異或”結果為 0，是這兩個數值相等的必要充分條件，可以作為判斷兩個變數是否相等的條件。

接下來，我們來學習一下，在程式碼中如何實現二進位制的邏輯操作。Java 中使用|表示按位的“或”，& 表示按位“與”，^ 表示按位“異或”。

import java.math.BigInteger;

public class Lesson1_3 {

/**
* @Description: 二進位制按位“或”的操作
* @param num1- 第一個數字，num2- 第二個數字
* @return 二進位制按位“或”的結果
*/
public static int or(int num1, int num2) {

return (num1 | num2);

}

/**
* @Description: 二進位制按位“與”的操作
* @param num1- 第一個數字，num2- 第二個數字
* @return 二進位制按位“與”的結果
*/
public static int and(int num1, int num2) {

return (num1 & num2);

}

/**

* @Description: 二進位制按位“異或”的操作
* @param num1- 第一個數字，num2- 第二個數字
* @return 二進位制按位“異或”的結果
*/

public static int xor(int num1, int num2) {

return (num1 ^ num2);

}


}
同樣，我們寫一段測試程式碼，驗證一下上面三個函式。

public static void main(String[] args) {

int a = 53;
int b = 35;

System.out.println(String.format(" 數字 %d(%s) 和數字 %d(%s) 的按位‘或’結果是 %d(%s)",
a, decimalToBinary(a), b, decimalToBinary(b), Lesson2_3.or(a, b), decimalToBinary(Lesson1_3.or(a, b)))); // 獲取十進位制數 53 和 35 的按位“或”

System.out.println(String.format(" 數字 %d(%s) 和數字 %d(%s) 的按位‘與’結果是 %d(%s)",
a, decimalToBinary(a), b, decimalToBinary(b), Lesson2_3.and(a, b), decimalToBinary(Lesson1_3.and(a, b)))); // 獲取十進位制數 53 和 35 的按位“與”

System.out.println(String.format(" 數字 %d(%s) 和數字 %d(%s) 的按位‘異或’結果是 %d(%s)",
a, decimalToBinary(a), a, decimalToBinary(a), Lesson2_3.xor(a, a), decimalToBinary(Lesson1_3.xor(a, a)))); // 獲取十進位制數 53 和 35 的按位“異或”

}


這段程式碼的執行結果是：數字 53(110101) 和數字 35(100011) 的按位‘或’結果是 55(110111)，數字 53(110101) 和數字 35(100011) 的按位‘與’結果是 33(100001)，數字 53(110101) 和數字 53(110101) 的按位‘異或’結果是 0(0)。

小結
今天我們聊了二進位制，你可能會問：學習二進位制究竟有什麼用呢？平時的程式設計中，我們好像並沒有使用相關的知識啊？確實，目前的高階語言可以幫助我們將人類的思維邏輯轉換為使用 0 和 1 的機器語言，我們不用再為此操心了。但是，二進位制作為現代計算機體系的基石，這些基礎的概念和操作，你一定要非常瞭解。

二進位制貫穿在很多常用的概念和思想中，例如邏輯判斷、二分法、二叉樹等等。邏輯判斷中的真假值就是用二進位制的 1 和 0 來表示的；二分法和二叉樹都是把要處理的問題一分為二，正好也可以通過二進位制的 1 和 0 來表示。因此，理解了二進位制，你就能更加容易地理解很多計算機的資料結構和演算法，也為我們後面的學習打下基礎。