深度學習基礎系列(五)| 深入理解交叉熵函式及其在tensorflow和keras中的實現
在統計學中,損失函式是一種衡量損失和錯誤(這種損失與“錯誤地”估計有關,如費用或者裝置的損失)程度的函式。假設某樣本的實際輸出為a,而預計的輸出為y,則y與a之間存在偏差,深度學習的目的即是通過不斷地訓練迭代,使得a越來越接近y,即 a - y →0,而訓練的本質就是尋找損失函式最小值的過程。
常見的損失函式為兩種,一種是均方差函式,另一種是交叉熵函式。對於深度學習而言,交叉熵函式要優於均方差函式,原因在於交叉熵函式配合輸出層的啟用函式如sigmoid或softmax函式能更快地加速深度學習的訓練速度。這是為什麼呢?讓我們來詳細瞭解下。
一、函式定義
1. 第一種損失函式:均方差函式,其定義為:
L(a, y) = ½ (a - y)2
令y=0,則L(a, y) = ½ a2 ,當a處於(-1, 1)區間範圍時,其圖形特徵為:
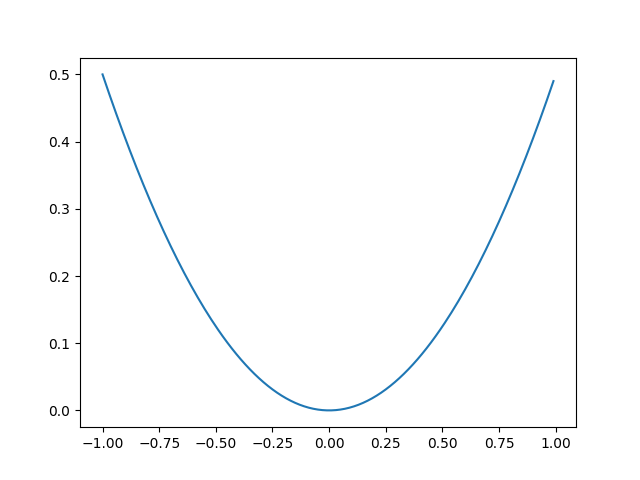
可以看出當y = 0, a =0時,L(a, y) →0,其值是最小的。
其求導公式為:dL(a, y) / da = a - y, 從函式本身來看當a = y時,L' (a, y) = 0,也即求得最小值。
2. 第二種損失函式:交叉熵函式,其定義為:
L(a, y) = - [y * ln a + (1 - y) ln (1 - a)]
為什麼該函式能幫我們找到最小值呢?假設a和y都是在(0, 1)這個區間內取值。
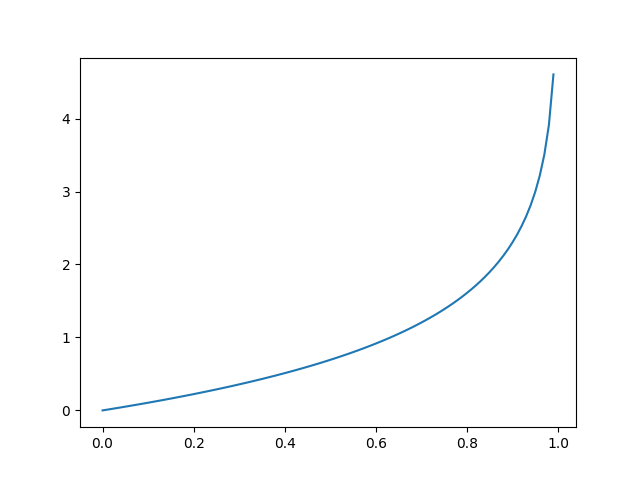
令 y=0, 則 L(a, y) = - ln (1 - a), 當a →0時, L(a, y) ≈ - ln 1 = 0
當a →1時, L(a, y) ≈ - ln 0 = +∞
故y=0, a=0時,L(a, y) →0,符合找到最小值的目標。圖形解釋如下:
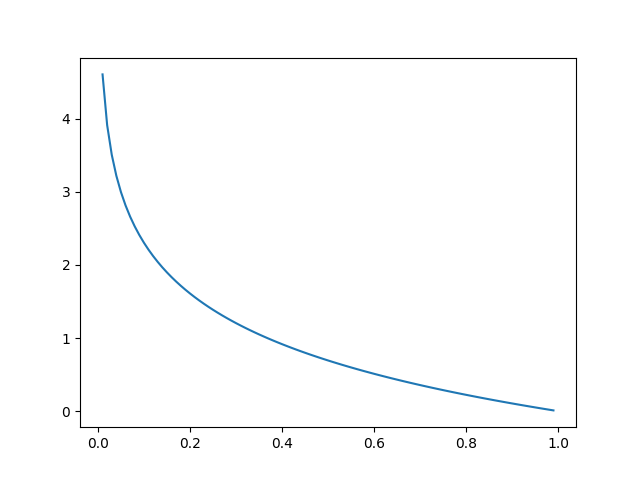
反之,令 y=1, 則 L(a, y) = - ln a, 當a →0時, L(a, y) ≈ - ln 0 = +∞
當a →1時, L(a, y) ≈ - ln 1 = 0
故y=1, a=1時,L(a, y) →0,也符合找到最小值的目標。圖形解釋如下:
當然,我們也可以令y=0.5,則 L(a, y) = -[0.5 * ln a + 0.5 * ln (1 - a)]。
同樣可以繪製出其圖形:
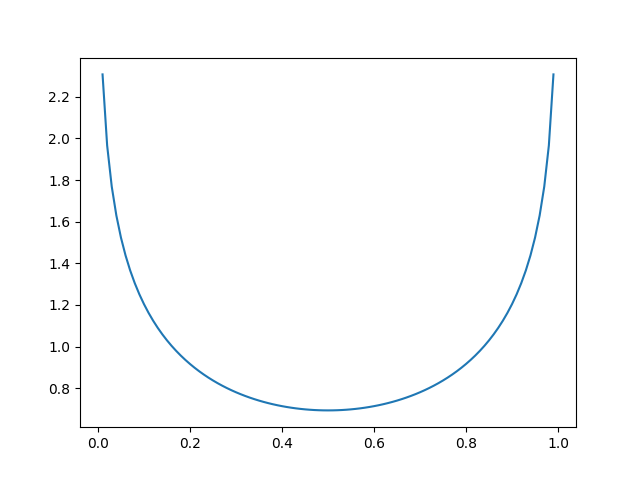
可以發現,當y=0.5, a=0.5時, L(a, y) →0,也符合找到最小值的目標。
以上描述簡單地證明交叉熵函式是一個有效尋找最小值目標的損失函式。
以下程式碼可以簡單地繪製出上述交叉熵函式的圖形特徵:
import numpy as np import matplotlib.pyplot as plt def loss_5(x): return -0.5 * np.log(x) - 0.5 * np.log(1 - x) def loss_0(x): return -1 * np.log(1 - x) def loss_1(x): return -1 * np.log(x) x = np.arange(0, 1, 0.01) y = loss_5(x) plt.plot(x, y) plt.show()
最後,我們來求導下交叉熵函式,以為後續證明用:
dL(a, y)/da = (- [y * ln a + (1 - y) ln (1 - a)])'
= -(y / a + (-1) * (1 -y) / (1 - a))
= - y / a + (1- y) / (1 - a )
= (a - y) / [a * (1 - a)]
二、為什麼交叉熵函式優於均方差函式?
前面的內容已讓我們瞭解兩種函式的特點,現在讓我們看看為什麼交叉熵函式要優於均方差函式。我們知道深度學習的訓練過程是通過梯度下降法反向傳播更新引數值,具體來說,每一次前向傳播結束後,通過對損失函式+啟用函式反向在每一層對每個w和b引數進行求導,得到dL/dw和dL/db的值,最後更新w和b,即 w → w - λ * dL/dw,b → b - λ * dL/db,其中λ為學習率。
我們假設啟用函式定義為sigmoid函式,並有如下前向傳播路徑:
z1 = w1 x + b1
a1= sigmoid(z1)
z2= w2 a1 + b2
a2= sigmoid(z2)
在此條件下,我們看看均方差函式和交叉熵函式在反向傳播上的求導結果:
1. 均方差函式+sigmoid函式的反向求導:
令L(a, y) = ½ (a - y)2 ,由前述可知,其求導為:L'(a, y) = a - y
而啟用函式sigmoid的求導為:a' (z)= a (1 - a)
我們對w2進行求導,由鏈式法則可知:
dL/dw2 = dL/da2 * da2/dz2 * dz2/dw2
= (a2 - y) * a2(1 - a2) * a1
2. 交叉熵函式+sigmoid函式的反向求導:
令L(a, y) = - [y * ln a + (1 - y) ln (1 - a)],其求導為:L'(a, y) = (a - y) / [a * (1 - a)]
同樣啟用函式sigmoid的求導為:a' (z)= a (1 - a)
我們依舊對w2進行求導,由鏈式法則可知:
dL/dw2 = dL/dσ2 * dσ2/dz2 * dz2/dw2
= (a2 - y) / [a2 * (1 - a2)] * a2(1 - a2) * a1
= (a2 - y) * a1
比較上述兩個反向求導w2的結果,有沒有發現交叉熵函式的求導結果要更簡潔,因為它沒有 a2(1 - a2) 這一項,即輸出層啟用函式a2的自身求導。沒有它非常重要,通過前文深度學習基礎系列(三)| sigmoid、tanh和relu啟用函式的直觀解釋, 我們可知啟用函式的自身斜率在趨近兩端時變得很平滑,這也意味著反向求導時迭代值dL/dw會比較小,從而使得訓練速度變慢,這即是交叉熵函式優於均方差函式的原因。
也許大家會問,在sigmoid函式上交叉熵函式佔優,那在softmax函式上又表現如何呢?我們繼續驗證,前向傳播圖作如下改造:
z1 = w1 x + b1
a1= sigmoid(z1)
z2= w2 a1 + b2
a2= softmax(z2)
假設softmax最後的輸出結果a2是由三個分類值組成,即y1 + y2 + y3 = 1,三種分類的概率和為1,其中y1 概率為0.9,y2 概率為0.05,y3 的概率為0.05。自然,我們希望某個分類的概率最接近1,以說明這個分類就是我們的預測值,因此可認為y = 1。 而啟用函式softmax,參考前文深度學習基礎系列(四)| 理解softmax函式,
令y1 = ex1 / (ex1 + ex2 + ex3 )
y2 = ex2 / (ex1 + ex2 + ex3 )
y3 = ex3 / (ex1 + ex2 + ex3 )
可知其求導為:
dy1/dx1= y1 (1 - y1)
dy2/dx1= - y1* y2
dy3/dx1= - y1* y3
在此條件下,我們看看均方差函式和交叉熵函式在反向傳播上的求導結果:
3. 均方差函式+softmax函式的反向求導:
若在y1進行反向求導,令L(y1, y) = ½ (y1 - y)2 ,其求導為:L'(y1, y) = y1 - y = y1 - 1
我們對w2進行求導,由鏈式法則可知:
dL/dw2 = dL/dy1* dy1/dz2 * dz2/dw2
= (y1 - 1) * y1(1 - y1) * a1
另一方面,若在y2進行反向求導,令L(y2, y) = ½ (y2 - y)2 ,其求導為:L'(y2, y) = y2 - y = y2 - 1
我們對w2進行求導,由鏈式法則可知:
dL/dw2 = dL/dy2* dy2/dz2 * dz2/dw2
= (y2 - 1) * (- y1 * y2) * a1
4. 交叉熵函式+softmax函式的反向求導:
若在y1進行反向求導,令 - [y * ln y1 + (1 - y) ln (1 - y1)],其求導為:L'(y1, y) = (y1 - y) / [y1 * (1 - y1)] = (y1 - 1) / [y1 * (1 - y1)] = -1/y1
我們對w2進行求導,由鏈式法則可知:
dL/dw2 = dL/dy1* dy1/dz2 * dz2/dw2
= -1/y1 * y1(1 - y1) * a1
= - (1 - y1) * a1
另一方面,若在y2進行反向求導,令 - [y * ln y2 + (1 - y) ln (1 - y2)],其求導為:L'(y2, y) = (y2 - y) / [y2 * (1 - y2)] = (y2 - 1) / [y2 * (1 - y2)] = -1/y2
我們對w2進行求導,由鏈式法則可知:
dL/dw2 = dL/dy2* dy2/dz2 * dz2/dw2
= -1/y2 * (- y1 * y2) * a1
= y1 * a1
綜上比較,交叉熵函式在反向求導中,依舊完美地避開了softmax函式自身導數的影響,還是優於均方差函式。
還需補充的是,在反向傳播過程中,每一層對w和b求導,通過鏈式法則可知,依舊會受到該層的啟用函式影響,若為sigmoid函式,依然不可避免地降低學習速度。因此深層網路中隱藏層的啟用函式目前大都為relu函式,可以確保其導數要麼為0,要麼為1。
三、交叉熵函式在tensorflow和keras的實現說明
1. sigmoid + 交叉熵函式
說明:可應用於二元分類,如判斷一張圖片是否為貓;但如果圖片裡有多個分類,也並不互斥,比如一張圖片裡既包含狗,也包含貓,但如果我們給了貓和狗兩個標籤,那判斷這張圖片,既可以認為是狗,也可以認為是貓。
官網已給出數學推導後的公式:
L = max(x, 0) - x * z + log(1 + exp(-abs(x))),其中x可認為是logits,z可認為是labels
舉一個簡單的例子:
import keras.backend as K from tensorflow.python.ops import nn y_target = K.constant(value=[1]) y_output = K.constant(value=[1]) print("y_target: ", K.eval(y_target)) print("y_output: ", K.eval(y_output)) print("the loss is: ", K.eval(nn.sigmoid_cross_entropy_with_logits(labels=y_target, logits=y_output)))
結果為:
y_target: [1.] y_output: [1.] the loss is: [0.3132617]
可以把引數帶入公式驗證:max(1, 0) - 1 * 1 + log(1 + exp(-abs(1))) = ln(1 + e-1) = 0.3132617
而在keras上體現為binary_crossentropy,用途與上面的sigmoid_cross_entropy_with_logits是一樣的,但兩者有差別:
sigmoid_cross_entropy_with_logits還原了預計值和輸出值在數學公式中的差值,但不是一種概率差。上述例子中,輸出值和預計值明明一樣,概率差應該為0,但結果卻為0.3132617
而binary_crossentropy則先把輸出值進行概率包裝後,再帶入sigmoid_cross_entropy_with_logits數學公式中。
舉一個例子:
import keras.backend as K from tensorflow.python.ops import math_ops from tensorflow.python.ops import clip_ops from tensorflow.python.framework import ops y_target = K.constant(value=[1]) y_output = K.constant(value=[1]) print("y_target: ", K.eval(y_target)) print("y_output: ", K.eval(y_output)) epsilon_ = ops.convert_to_tensor(K.epsilon(), y_output.dtype.base_dtype) print("epsilon: ", K.eval(epsilon_)) output = clip_ops.clip_by_value(y_output, epsilon_, 1 - epsilon_) print("output: ", K.eval(output)) output = math_ops.log(output / (1 - output)) print("output: ", K.eval(output))
print("the loss is: ", K.eval(nn.sigmoid_cross_entropy_with_logits(labels=y_target, logits=output)))
結果為:
y_target: [1.] y_output: [1.] epsilon: 1e-07 output: [0.9999999] output: [15.942385] the loss is: [1.1920933e-07]
最後的結果1.1920933e-07相當於0.00000012,符合我們對預測值和輸出值差別不大的認知。因此可以理解keras的損失函式輸出值更加人性化。
2. softmax + 交叉熵函式
說明:可用於多元分類,如判斷一張圖片是否為貓;但如果圖片裡多個類別則是互斥的,比如一張圖片裡既包含狗,也包含貓,那我們也只能給唯一的標籤,要麼是狗,要麼是貓。
其數學公式為:L = ∑ -(y * lna)
舉個例子說明:
import keras.backend as K from tensorflow.python.ops import nn y_target = K.constant(value=[1, 2]) y_output = K.constant(value=[1, 2]) print("y_target: ", K.eval(y_target)) print("y_output: ", K.eval(y_output)) print("the loss is: ", K.eval(nn.softmax_cross_entropy_with_logits_v2(labels=y_target, logits=y_output)))
結果為:
y_target: [1. 2.] y_output: [1. 2.] the loss is: 1.939785
說明:y_output有兩個輸出值1和2,通過softmax函式轉化後,我們可知1的對應softmax值為0.268941422,而2的對應softmax值為0.731058581;同時1對應的預測值為1,2對應的預測值為2。將上述值帶入公式驗證:
L = ∑ -(y * lna)
= -(1 * ln (e/ (e + e2)) ) + -(2 * ln (e2 / (e + e2)))
= -(1* ln0.268941422) + -(2 * ln0.731058581)
= 1.939785
而在keras中,與此對應的是categorical_crossentropy,採用的演算法和上述基本一致,只是需要把y_output按分類值做概率轉換。
我們來舉例說明:
import keras.backend as K from tensorflow.python.ops import nn from tensorflow.python.ops import math_ops from tensorflow.python.ops import clip_ops from tensorflow.python.framework import ops y_target = K.constant(value=[1, 2]) y_output = K.constant(value=[1, 2]) print("y_target: ", K.eval(y_target)) print("y_output: ", K.eval(y_output)) output = y_output / math_ops.reduce_sum(y_output, -1, True) print("output: ", K.eval(output)) epsilon_ = ops.convert_to_tensor(K.epsilon(), output.dtype.base_dtype) output = clip_ops.clip_by_value(output, epsilon_, 1. - epsilon_) print("output: ", K.eval(output)) print("the loss is: ", K.eval(-math_ops.reduce_sum(y_target * math_ops.log(output), -1)))
結果為:
y_target: [1. 2.] y_output: [1. 2.] output: [0.33333334 0.6666667 ] output: [0.33333334 0.6666667 ] the loss is: 1.9095424
其計算公式為:
L = ∑ -(y * lna)
= -(1 * ln 0.33333334 ) + -(2 * ln 0.66666667)
= 1.9095424
3. sparse + softmax + 交叉熵函式:
說明:可用於多元分類,如判斷一張圖片是否為貓;但如果圖片裡多個類別則是互斥的,比如一張圖片裡既包含狗,也包含貓,那我們也只能給唯一的標籤,要麼是狗,要麼是貓。
加上sparse的區別在於:不加sparse給定的labels是允許有概率分佈的,如[0.3, 0.4, 0.2, 0.05, 0.05],而加sparse,則如其名sparse稀疏矩陣,概率只允許要麼存在,要麼不存在,如[0, 0, 0, 1, 0]
我們常見的mnist資料集、cifar-10資料集等都是這種型別。
其數學公式為:L = -y * ln a,其中a為概率為1的輸出值
依舊舉例說明:
import keras.backend as K from tensorflow.python.ops import nn y_target = K.constant(value=1, dtype='int32') y_output = K.constant(value=[1, 2]) print("y_target: ", K.eval(y_target)) print("y_output: ", K.eval(y_output)) print("the loss is: ", K.eval(nn.sparse_softmax_cross_entropy_with_logits(labels=y_target, logits=y_output)))
結果為:
y_target: 1 y_output: [1. 2.] the loss is: 0.31326166
說明:本例中,輸出值y_output為1和2,表示兩種分類,而y_target的值為1,表示為分類的index,也就是對應了輸出值2;更直白地說,輸出值1的概率為0,輸出值2的概率為1。
具體計算方式為:a = e2 / (e + e2) = 0.731058581
L = - ln a = 0.313261684
而在keras中,與此對應的為sparse_categorical_crossentropy,該函式會呼叫上述函式,最大的不同在於:1. 其引數y_output被設定為經過softmax之後的值;2. y_output還會被log處理下
舉個例子:
import keras.backend as K y_target = K.constant(value=1, dtype='int32') y_output = K.constant(value=[0.2, 0.2, 0.6]) print("y_target: ", K.eval(y_target)) print("y_output: ", K.eval(y_output)) print("the loss is: ", K.eval(K.sparse_categorical_crossentropy(y_target, y_output)))
結果為:
y_target: 1 y_output: [0.2 0.2 0.6] the loss is: [1.609438]
說明:本例中y_output的值已經假設按照softmax處理後的值:0.2,0.2和0.6
其計算方式為:
a = eln0.2/(eln0.2 + eln0.2+ eln0,6) = 0.2/(0.2 + 0.2 +0.6) = 0.2
L = - ln 0.2 = 1.609438
以上即是交叉熵函式作為損失函式的使用理由,及其在tensorflow和keras中的實現說明。
