求兩個頂點間的最短路徑

相關資料結構

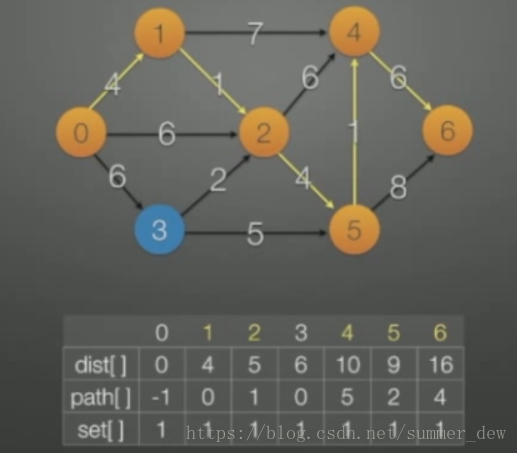
• dist[v]：起點到結點v的最短路徑的距離為dist[v]
• path[v]：起點到結點v的最短路徑path中，結點v的前一個結點為path[v] 【特殊值】path[v]=-1：起點到v的最短路徑中，v沒有前一個結點了
• set[v]：v已併入則set[v]=1

【結果解釋】以下所說最短路徑都是逆序，是path[v]往上找的結果

1. 起點0到結點6的最短路徑 path[6]=4，path[4]=5，path[5]=2，path[2]=1，path[1]=0，path[0]=-1停止 即0到6的最短路徑為：6->4->5->2->1->0
2. 起點0到結點5的最短路徑 path[5]=2，path[2]=1，path[1]=0，path[0]=-1停止 即0到5的最短路徑為：5->2->1->0
3. 0–>4的最短路徑 path[4]=5，path[5]=2，path[2]=1，path[1]=0，path[0]=-1停止 即0到6的最短路徑為：4->5->2->1->0
4. 0–>3的最短路徑 path[3]=0，path[0]=-1停止 即0到3的最短路徑為：3->0
5. 0–>2的最短路徑 path[2]=1，path[1]=0，path[0]=-1結束 即0到2的最短路徑為：2->1->0
6. 0–>1的最短路徑 path[1]=0，path[0]=-1結束 即0到1的最短路徑為：1->0

實現

【測試資料】 【結果】 【函式】

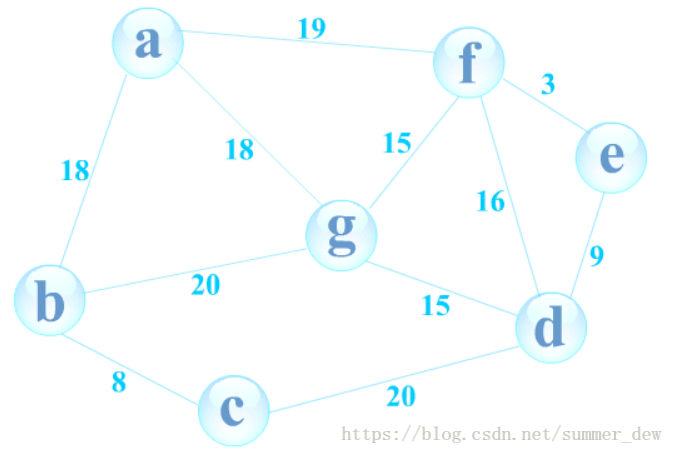
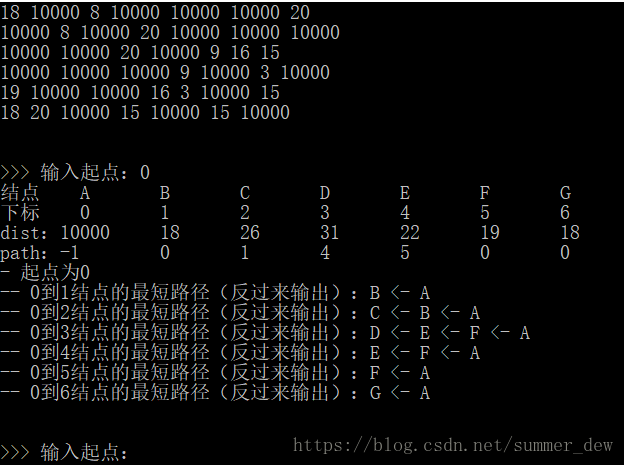
void Dijkstra(int n, int MGraph[][maxSize], int start, int dist[], int path[]) {
	int set[maxSize];
	int min,v;
	int i,j;
	
	//初始化
	for (i=0; i<n; i++) {
		dist[i]=MGraph[start][i];
		set[i]=0;
		if (MGraph[start][i]<INF)
			path[i]= start;
		else
			path[i]=-1;
	}
	set[start]
 
=1;path[start]=-1;

	//對剩餘的每個頂點進行處理
	for (i=0; i<n-1; ++i) {
		//選出與起點距離最近的點
		min=INF;
		for (j=0; j<n; j++) {
			if (set[j]==0 && dist[j]<min) {
				v=j;
				min=dist[j];
			}
		}
		set[v]=1;
	
		//對dist、path更新
		for (j=0; j<n; ++j) {
			if (set[j]==0 && dist[v]+MGraph[v][j]<dist[j]) {
				dist[j]=dist[v]+MGraph[v][j];
				path[j]=v;
			}
		}
	}
}

完整程式碼

#include<stdio.h>
#include<stdlib.h>

#define maxSize 10
#define INF 100000

void Dijkstra(int n, int MGraph[][maxSize], int start, int dist[], int path[]) {
	int set[maxSize];
	int min,v;
	int i,j;
	
	//初始化
	for (i=0; i<n; i++) {
		dist[i]=MGraph[start][i];
		set[i]=0;
		if (MGraph[start][i]<INF)
			path[i]= start;
		else
			path[i]=-1;
	}
	set[start]=1;path[start]=-1;

	//對剩餘的每個頂點進行處理
	for (i=0; i<n-1; ++i) {
		//選出與起點距離最近的點
		min=INF;
		for (j=0; j<n; j++) {
			if (set[j]==0 && dist[j]<min) {
				v=j;
				min=dist[j];
			}
		}
		set[v]=1;
	
		//對dist、path更新
		for (j=0; j<n; ++j) {
			if (set[j]==0 && dist[v]+MGraph[v][j]<dist[j]) {
				dist[j]=dist[v]+MGraph[v][j];
				path[j]=v;
			}
		}
	}
}

int MGraph[maxSize][maxSize]; //鄰接矩陣
char vertex[maxSize];
int main() {
/*
7
ABCDEFG
10000 18 10000 10000 10000 19 18
18 10000 8 10000 10000 10000 20
10000 8 10000 20 10000 10000 10000
10000 10000 20 10000 9 16 15
10000 10000 10000 9 10000 3 10000
19 10000 10000 16 3 10000 15
18 20 10000 15 10000 15 10000
0
*/
	int n;
	int i,j;
	char tmp[maxSize+5];
	int start,end;
	int dist[maxSize],path[maxSize];

	scanf("%d", &n); //結點數
	scanf("%s", tmp); //結點資訊
	for (i=0; i<n; i++)
		vertex[i] = tmp[i];
	for (i=0; i<n; i++) { //矩陣
		for (j=0; j<n; j++) {
			scanf("%d", &MGraph[i][j]);
		}
	}
	while (1) {
		printf("\n\n>>> 輸入起點：");
		scanf("%d" , &start); //輸入兩個測試的頂點，求v->w的最短路徑
		Dijkstra(n, MGraph, start, dist, path);

		printf("結點\t");
		for (i=0; i<n; i++) {
			printf("%c\t", vertex[i]);
		}
		printf("\n下標\t");
		for (i=0; i<n; i++) {
			printf("%d\t", i);
		}
		printf("\ndist：");
		for (i=0; i<n; i++) {
			printf("%d\t", dist[i]);
		}
		printf("\npath：");
		for (i=0; i<n; i++) {
			printf("%d\t", path[i]);
		}
		printf("\n- 起點為%d\n", start);
		for (end=1; end<n; end++) {
			printf("-- %d到%d結點的最短路徑（反過來輸出）：", start, end);
			for (i=end; path[i]!=-1; i=path[i]) {
				printf("%c <- ", vertex[i]);
			}
			printf("%c\n", vertex[i]);
		}
	}

	return 0;
}