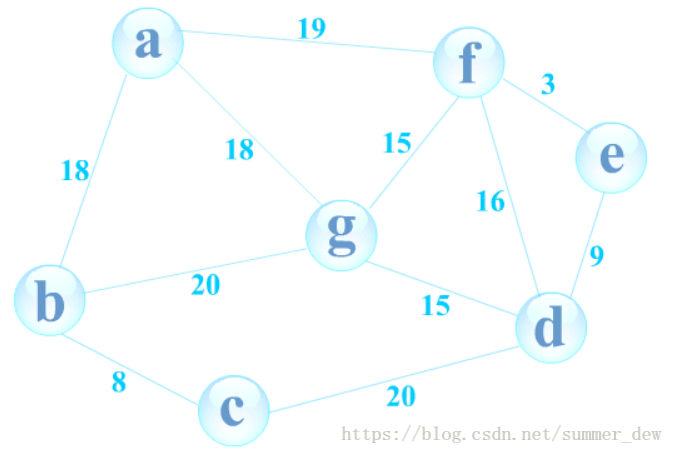
[圖] 6.3.1 Floyd演算法|佛洛依德
阿新 • • 發佈:2018-12-15
文章目錄
測試資料
結果
實現
void PrintPath(int u, int v, int path[][maxSize]) {
int mid;
if (path[u][v]==-1) {
//直接輸出,沒有中間點
printf("<%c,%c> ", vertexs[u], vertexs[v]);
} else { //有中間點
mid = path[u][v];
PrintPath(u, mid, path);
PrintPath(mid, v, path);
}
}
void Floyd(int n, int MGraph[ 舉例:每一步執行
【工作原理】
完整程式碼
#include<stdio.h>
#include<stdlib.h>
#define maxSize 10
#define INF 100
int MGraph[maxSize][maxSize]; //鄰接矩陣
char vertexs[maxSize]; //結點資訊
void PrintPath(int u, int v,