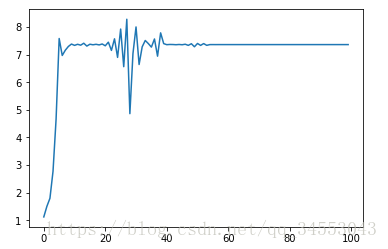
深度學習總結二:優化器
阿新 • • 發佈:2018-12-15
對應程式碼
梯度下降
附梯度下降w變化曲線用於對比
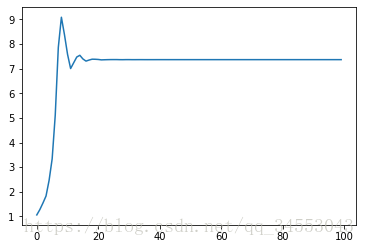
momentum
動量法,原理在於一個方向的速度可以積累,而且越積累越大;通過不同訓練樣本求得梯度時,在最優的方向的梯度,始終都會增大最優方向上的速度。因此,可以減少許多震盪。 對用程式碼:
self.w_update = self.gamma * self.w_update + (1 - self.gamma) * w_grad
Ada
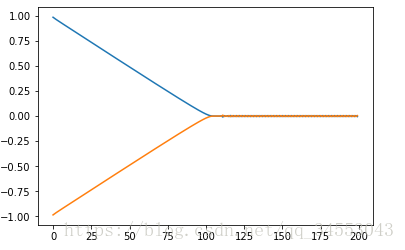
假設存在w1和w2,且兩者更新速度不一致。如下圖:
self.s += 
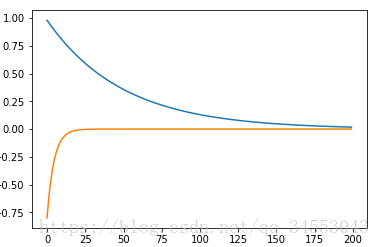
RMSProp
RMSProp原理:測試初期因為加了s_correct所以擬合速度會加快,用動量的流平均思想,到了一定時間,總的里程開始不變,解決Ada後期效率低迷問題。 對應程式碼:
self.s = self.beta * self.s + (1 - self.beta) * (w_grad**2)
s_correct = self. Adam
集合前面幾個演算法的優點 對應程式碼:
self.v = self.gamma * self.v + (1 - self.gamma) * w_grad
v_correct = self.v / (1 - self.gamma ** (i+1))
self.s = self.beta * self.s + (1 - self.beta) * (w_grad**2)
s_correct = self.s/(1 - self.