【NOIP2018Day1T2】【洛谷P5020】貨幣系統
問題描述
在網友的國度中共有 n 種不同面額的貨幣,第 i 種貨幣的面額為 a[i],你可以假設每一種貨幣都有無窮多張。為了方便,我們把貨幣種數為 n、面額陣列為 a[1..n] 的貨幣系統記作 (n,a)。
在一個完善的貨幣系統中,每一個非負整數的金額 x 都應該可以被表示出,即對每一個非負整數 x,都存在 n 個非負整數 t[i] 滿足 a[i]×t[i] 的和為 x。然而, 在網友的國度中,貨幣系統可能是不完善的,即可能存在金額 x 不能被該貨幣系統表示出。例如在貨幣系統 n=3, a=[2,5,9] 中,金額 1,3 就無法被表示出來。
兩個貨幣系統 (n,a) 和 (m,b) 是等價的,當且僅當對於任意非負整數 x,它要麼均可以被兩個貨幣系統表示出,要麼不能被其中任何一個表示出。
現在網友們打算簡化一下貨幣系統。他們希望找到一個貨幣系統 (m,b),滿足 (m,b) 與原來的貨幣系統 (n,a)等價,且 m 儘可能的小。他們希望你來協助完成這個艱鉅的任務:找到最小的 m。
輸入格式
輸入檔案的第一行包含一個整數 T,表示資料的組數。
接下來按照如下格式分別給出 T 組資料。 每組資料的第一行包含一個正整數 n。接下來一行包含 n 個由空格隔開的正整數 a[i]。
輸出格式
輸入檔案的第一行包含一個整數 T,表示資料的組數。
接下來按照如下格式分別給出 T 組資料。 每組資料的第一行包含一個正整數 n。接下來一行包含 n 個由空格隔開的正整數 a[i]。
樣例輸入
2
4
3 19 10 6
5
11 29 13 19 17
樣例輸出
2
5
提示
在第一組資料中,貨幣系統 (2,[3,10]) 和給出的貨幣系統 (n,a) 等價,並可以驗證不存在 m<2 的等價的貨幣系統,因此答案為 2。 在第二組資料中,可以驗證不存在 m<n 的等價的貨幣系統,因此答案為 5。
資料範圍
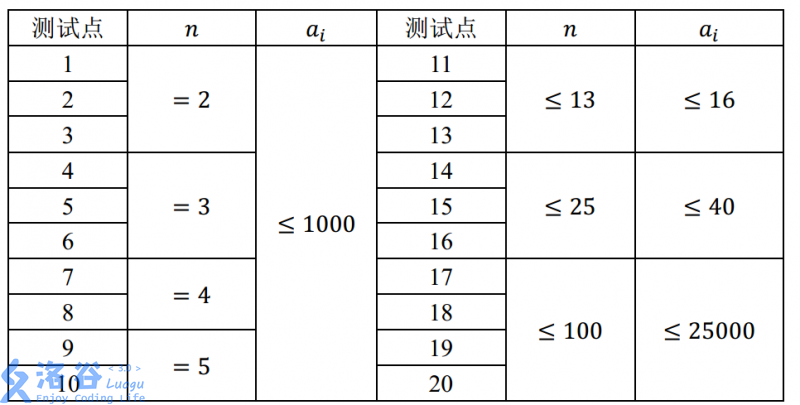
題解
研究一下樣例,發現新貨幣系統是舊貨幣系統的子集。於是大膽猜想:新貨幣系統一定是舊貨幣系統刪掉幾種面額的貨幣,並且被刪掉的面額可以被沒被刪掉的面額表示出來。
(遵循大膽猜想不用證明原則的大佬自動跳過這段)
證明:反證法
反正就是這樣
證明完畢
如果以上結論不成立,無非存在以下兩種情況:
1、新貨幣系統中存在舊貨幣系統所沒有的面額,記為a[i],a[i]不能被舊貨幣系統表示出來
2、新貨幣系統中存在舊貨幣系統所沒有的面額,記為a[j], a[j]能夠被舊貨幣系統表示出來
對於第一種情況,顯然新貨幣系統可以表示出舊貨幣系統所表示不出的面額,因為a[i]本身就是一種舊貨幣系統所表示不出的面額,於是這種情況不成立。
對於第二種情況,顯然a[j]是多餘的,因為a[j]能夠被表示出來,所以需要用到a[j]時可以用表示出a[j]的這些面額代替,所以a[j]可以刪掉,於是這種情況也不成立。
所以,上述結論:新貨幣系統一定是舊貨幣系統刪掉幾種面額的貨幣,並且被刪掉的面額可以被沒被刪掉的面額表示出來成立。
那麼我們只需要求給定貨幣系統最多可以刪掉多少種面額。
設f[i]表示面額為i能否被表示出來,則
f[i]=f[i]|f[j](1<=j<k,a[k]<i)
在動規迴圈時順便計算f[i]==false && i∈a的個數,用總數減去f[i]==false && i∈a的個數,就是答案
時間複雜度 5*107
1 #include <algorithm> 2 #include <cstring> 3 #include <cstdio> 4 int T,n,m,a[105]; 5 bool f[25005]; 6 int main() 7 { 8 9 int i,j,k; 10 scanf("%d",&T); 11 while (T--) 12 { 13 scanf("%d",&n); 14 for (i=1;i<=n;i++) scanf("%d",&a[i]); 15 m=n; 16 std::sort(a+1,a+n+1); 17 memset(f,0,sizeof(f)); 18 f[a[1]]=1; k=1; 19 for (i=a[1]+1;i<=a[n];i++) 20 { 21 for (j=1;j<=k && !f[i];j++) 22 f[i]=f[i]|f[i-a[j]]; 23 if (i==a[k+1]) 24 { 25 k++; 26 if (f[i]) m--; 27 else f[i]=1; 28 } 29 } 30 printf("%d\n",m); 31 } 32 return 0; 33 }
