一、題目描述

In the video game Fallout 4, the quest “Road to Freedom” requires players to reach a metal dial called the “Freedom Trail Ring”, and use the dial to spell a specific keyword in order to open the door.

Given a string ring, which represents the code engraved on the outer ring and another string key

Initially, the first character of the ring is aligned at 12:00 direction. You need to spell all the characters in the string key one by one by rotating the ring clockwise or anticlockwise to make each character of the string key

At the stage of rotating the ring to spell the key character key[i]:

1. You can rotate the ring clockwise or anticlockwise one place, which counts as 1 step. The final purpose of the rotation is to align one of the string ring’s characters at the 12:00 direction, where this character must equal to the character key[i]
   .
2. If the character key[i] has been aligned at the 12:00 direction, you need to press the center button to spell, which also counts as 1 step. After the pressing, you could begin to spell the next character in the key (next stage), otherwise, you’ve finished all the spelling.

Example:

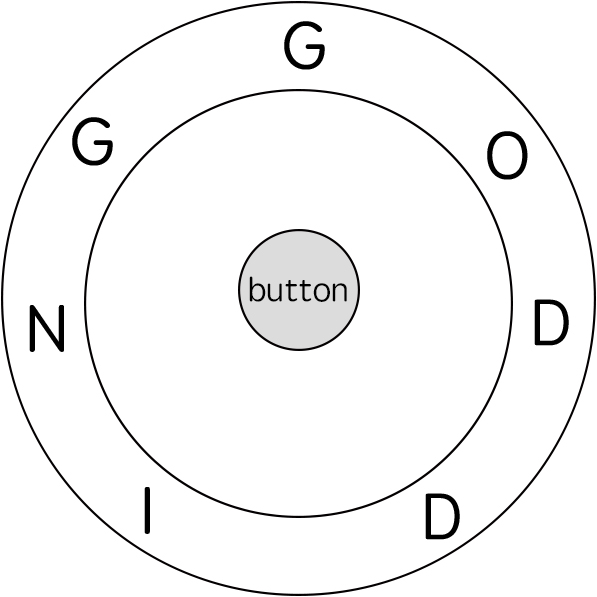
Input: ring = “godding”, key = “gd” Output: 4 Explanation: For the first key character ‘g’, since it is already in place, we just need 1 step to spell this character. For the second key character ‘d’, we need to rotate the ring “godding” anticlockwise by two steps to make it become “ddinggo”. Also, we need 1 more step for spelling. So the final output is 4.

Note:

1. Length of both ring and key will be in range 1 to 100.
2. There are only lowercase letters in both strings and might be some duplcate characters in both strings.
3. It’s guaranteed that string key could always be spelled by rotating the string ring.

二、題目分析

  根據題意，我們需要使用給出的 ring 字串拼出目標 key 字串，求出所需的操作步數。雖然按題目所說，按下按鈕即 spell 也算一個操作步數，但這部分總的步數就是 key.size() ，在最後加上即可，所以以下討論就忽略這個步驟。

  顧名思義，我們可以將 ring 字串看成一個簡單的環形圖，從一個字元轉到其他字元所需操作步數即為它們之間的距離，這裡用 $a_ib_j$ 表示 ring 中其中一個 a 字元到其中一個 b 字元的距離；並使用 $abc$ 表示拼成 "abc" 字串所需的最小運算元。   為了方便說明，這裡暫且使用字串 "abcd" 作為 key。考慮到最初的起點 ring[0] ，用 X 來代表，則 key 為 Xabcd 。

  先來看 key 的前兩個字元 Xa，若我們要求拼成它的最小運算元，那麼很簡單，只要取 $Xa = min( Xa_0, Xa_1, Xa_2, ..., Xa_n )$ 即可。   若我們再加上第三個字元 b ，在 ring 中有n個字元 b 的情況下，我們分兩步操作，①對於每一個“終點” $b_i$ ，求出從 X 出發到達該位置的 b 字元的距離，②再從它們之中選出一個最小的即可。在步驟①中我們要使用到 $Xa_0, Xa_1, ..., Xa_n$ 的資料，即到 $b_i$ 的距離為 $min( Xa_0 + a_0b_i, Xa_1 + a_1b_i, Xa_2 + a_2b_i, ..., Xa_n + a_nb_i )$，表示為 $Xab_i$ ，最後在這些最小值之中再求它們的最小值即可，即 $Xab = min( Xab_0, Xab_1, ..., Xab_n )$ 。   同理，若再加上第四個字元 c ，①對於每一個“終點” $c_i$ ，求出從 X 出發到達該位置的 c 字元的距離，②再從它們之中選出一個最小的即可。而在步驟①中同樣要用到 $Xab_0, Xab_1, ..., Xab_n$ 的資料，即到 $c_i$ 的距離為 $Xabc_i = min( Xab_0 + b_0c_i, Xab_1 + b_1c_i, Xab_2 + b_2c_i, ..., Xab_n + b_nc_i )$ 。   最後一個字元也是相同步驟，不再贅述。最終我們就可求得需要的 $Xabcd$ 。

  從以上分析可看出，這是一個自底向上的動態規劃問題。對於其他字串，也是相同的步驟求解。

三、具體實現

  按照分析，總的複雜度為$O(NL^2)$ ，其中 $N$ 為 key 的長度，$L$ 為 ring 的長度。   使用雜湊表 unordered_map 儲存 ring 中各個字母的下標（同個字母的不同位置），使用 vector<unordered_map<int, int>> 儲存類似 $Xa_0, Xa_1, ..., Xa_n, Xab_0, Xab_1, ..., Xab_n$ 這些資料。

class Solution
{
  public:
    int findRotateSteps( string ring, string key )
    {
        int **distance = new int*[ring.size()];
        for ( size_t i = 0; i < ring.size(); ++i )
            distance[i] = new int[ring.size()]();

        for ( int i = 0; i < ring.size(); ++i ) {
            for ( int j = 0; j < ring.size(); ++j ) {
                distance[i][j] = abs( j - i );
                if ( distance[i][j] > ring.size() / 2 )
                    distance[i][j] = ring.size() - distance[i][j];
            }
        }

        unordered_map<char, vector<int>> indexTable;
        for ( size_t i = 0; i < ring.size(); ++i )
            indexTable[ring.at( i )].push_back( i );

        vector<unordered_map<int, int>> result( key.size() );
        for ( int n : indexTable.at( key.at( 0 ) ) ) {
            result[0][n] = distance[0][n];
        }

        int minStep = INT_MAX;

        for ( size_t i = 1; i < key.size(); ++i ) {
            for ( int n : indexTable.at( key.at( i ) ) ) {

                int thisMin = INT_MAX;
                for ( auto p : result.at( i - 1 ) ) {
                    thisMin = min( thisMin, p.second + distance[p.first][n] );
                }
                result[i][n] = thisMin;

                if ( i == key.size() - 1 )
                    minStep = min( minStep, thisMin );

            }
        }

        for ( size_t i = 0; i < ring.size(); ++i )
            delete [] distance[i];
        delete [] distance;

        return minStep + key.size();
    }
};