Get the code: To follow along, all the code is also available as an iPython notebook on Github.

在這篇文章中，我們將從頭開始實現一個簡單的3層神經網路。我們不會得到所需的所有數學，但我會嘗試直觀地解釋我們正在做什麼。我還會指出資源，讓您瞭解詳細資訊。

在這裡，我假設您熟悉基本的微積分和機器學習概念，例如：你知道什麼是分類和正規化。理想情況下，您還可以瞭解梯度下降等優化技術的工作原理。但即使你不熟悉上述任何一篇文章，這篇文章仍然會變得有趣;）

但為什麼要從頭開始實施神經網路呢？即使您計劃將來使用像PyBrain這樣的神經網路庫，從頭開始實施網路至少一次也是非常有價值的練習。它可以幫助您瞭解神經網路的工作原理，這對於設計有效模型至關重要。

需要注意的一點是，這裡的程式碼示例並不是非常有效。它們意味著易於理解。在即將發表的文章中，我將探討如何使用Theano編寫有效的神經網路實現。 （更新：現已推出）

生成資料集

讓我們從生成我們可以使用的資料集開始。幸運的是，scikit-learn有一些有用的資料集生成器，因此我們不需要自己編寫程式碼。我們將使用make_moons函式。

# Generate a dataset and plot it
np.random.seed(0)
X, y = sklearn.datasets.make_moons(200, noise=0.20)
plt.scatter(X[:,0], X[:,1], s=40, c=y, cmap=plt.cm.Spectral)
 

我們生成的資料集有兩個類，繪製為紅色和藍色點。您可以將藍點視為男性患者，將紅點視為女性患者，x軸和y軸為醫學測量。

我們的目標是訓練機器學習分類器，該分類器在給定x和y座標的情況下預測正確的類（女性的男性）。請注意，資料不是線性可分的，我們不能繪製分隔兩個類的直線。這意味著線性分類器（如Logistic迴歸）將無法擬合數據，除非您手工設計適用於給定資料集的非線性要素（如多項式）。

事實上，這是神經網路的主要優勢之一。您無需擔心功能工程。神經網路的隱藏層將為您學習功能。

事實上，這是神經網路的主要優勢之一。您無需擔心功能工程。神經網路的隱藏層將為您學習功能。

Logistic迴歸

為了證明這一點，讓我們訓練一個Logistic迴歸分類器。它的輸入是x和y值，輸出是預測的類（0或1）。為了讓我們的生活更輕鬆，我們使用scikit-learn中的Logistic迴歸類。

# Train the logistic rgeression classifier

clf = sklearn.linear_model.LogisticRegressionCV()

clf.fit(X, y)


# Plot the decision boundary

plot_decision_boundary(lambda x: clf.predict(x))

plt.title("Logistic Regression")

該圖顯示了Logistic迴歸分類器學習的決策邊界。它使用直線將資料儘可能好地分離，但它無法捕獲資料的“月亮形狀”。

訓練神經網路

現在讓我們構建一個3層神經網路，其中包含一個輸入層，一個隱藏層和一個輸出層。輸入層中的節點數由我們的資料的維數確定.2。類似地，輸出層中的節點數由我們擁有的類的數量決定，也是2.（因為我們只有2個類實際上只有一個輸出節點可以預測為0或1，但是有2個可以讓以後更容易將網路擴充套件到更多的類）。網路的輸入將是x和y座標，其輸出將是兩個概

率，一個用於0級（“女性”），一個用於1級（“男性”）。它看起來像這樣：

我們可以選擇隱藏層的維度（節點數）。我們在隱藏層中放置的節點越多，我們能夠適應的功能就越複雜。但更高的維度需要付出代價。首先，需要更多的計算來進行預測並學習網路引數。更多引數也意味著我們更容易過度擬合數據。

如何選擇隱藏層的大小？雖然有一些一般的指導方針和建議，但它總是取決於您的具體問題，而更多的是藝術而不是科學。稍後我們將使用隱藏中的節點數來檢視它是如何影響我們的輸出的。

我們還需要為隱藏層選擇一個啟用函式。啟用功能將層的輸入轉換為其輸出。非線性啟用函式允許我們擬合非線性假設。啟用函式的常見chocies是tanh，sigmoid函式或ReLU。我們將使用tanh，它在許多場景中表現都很好。這些函式的一個很好的屬性是它們的派生可以使用原始函式值來計算。例如： tanh x的導數是1-  tanh ^ 2 x。這很有用，因為它允許我們計算一次tanh x並稍後重新使用它的值來獲得導數。

因為我們希望我們的網路輸出概率，所以輸出層的啟用函式將是softmax，這只是將原始分數轉換為概率的一種方式。如果您熟悉邏輯函式，您可以將softmax視為對多個類的推廣。

我們的網路如何進行預測

我們的網路使用前向傳播進行預測，這只是一堆矩陣乘法和我們在上面定義的啟用函式的應用。如果x是我們網路的二維輸入，那麼我們計算我們的預測（也是二維的），如下所示：

z_i是層i的輸入，a_i是應用啟用函式後的層i的輸出。 W_1，b_1，W_2，b_2是我們網路的引數，我們需要從我們的培訓資料中學習。您可以將它們視為在網路層之間轉換資料的矩陣。觀察上面的矩陣乘法，我們可以計算出這些矩陣的維數。如果我們為隱藏圖層使用500個節點，那麼。現在，如果我們增加隱藏層的大小，您就會明白為什麼我們有更多引數。

學習引數

學習網路引數意味著找到最小化訓練資料誤差的引數（W_1，b_1，W_2，b_2）。但是我們如何定義錯誤呢？我們將測量我們的錯誤的函式稱為損失函式。 softmax輸出的常見選擇是分類交叉熵損失（也稱為負對數似然）。如果我們有N個訓練樣例和C類，那麼關於真實標籤y的預測的損失由下式給出：

公式看起來很複雜，但它真正做的就是總結我們的訓練樣例，如果我們預測了不正確的類，就會增加損失。兩個概率分佈y（正確的標籤）和\ hat {y}（我們的預測）越遠，我們的損失就越大。通過找到最小化損失的引數，我們最大化了訓練資料的可能性。

我們可以使用梯度下降來找到最小值，我將實現最普遍的梯度下降版本，也稱為具有固定學習率的批量梯度下降。諸如SGD（隨機梯度下降）或小批量梯度下降之類的變化通常在實踐中表現更好。因此，如果你是認真的，你會想要使用其中一種，理想情況下你也會隨著時間的推移而衰減學習率。

作為輸入，梯度下降需要相對於我們的引數的損失函式的梯度（導數的向量）：。為了計算這些梯度，我們使用著名的反向傳播演算法，這是一種從輸出開始有效計算梯度的方法。我不會詳細介紹反向傳播的工作原理，但是網上有許多優秀的解釋(here or here) .

應用反向傳播公式，我們發現以下內容（相信我）：

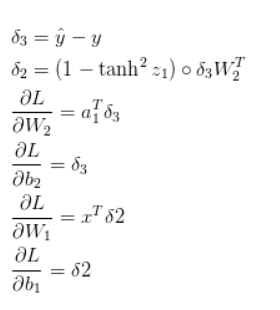
實現

現在我們已準備好實施。我們首先為梯度下降定義一些有用的變數和引數：

num_examples = len(X) # training set size

nn_input_dim = 2 # input layer dimensionality

nn_output_dim = 2 # output layer dimensionality


# Gradient descent parameters (I picked these by hand)

epsilon = 0.01 # learning rate for gradient descent

reg_lambda = 0.01 # regularization strength

首先讓我們實現上面定義的損失函式。我們用它來評估我們模型的表現：

# Helper function to evaluate the total loss on the dataset

def calculate_loss(model):

    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']

    # Forward propagation to calculate our predictions

    z1 = X.dot(W1) + b1

    a1 = np.tanh(z1)

    z2 = a1.dot(W2) + b2

    exp_scores = np.exp(z2)

    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

    # Calculating the loss

    corect_logprobs = -np.log(probs[range(num_examples), y])

    data_loss = np.sum(corect_logprobs)

    # Add regulatization term to loss (optional)

    data_loss += reg_lambda/2 * (np.sum(np.square(W1)) + np.sum(np.square(W2)))

    return 1./num_examples * data_loss

我們還實現了一個輔助函式來計算網路的輸出。它按照上面的定義進行前向傳播，並返回具有最高概率的類。

# Helper function to predict an output (0 or 1)

def predict(model, x):

    W1, b1, W2, b2 = model['W1'], model['b1'], model['W2'], model['b2']

    # Forward propagation

    z1 = x.dot(W1) + b1

    a1 = np.tanh(z1)

    z2 = a1.dot(W2) + b2

    exp_scores = np.exp(z2)

    probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)

    return np.argmax(probs, axis=1)

最後，這裡有訓練神經網路的功能。它使用我們在上面找到的反向傳播導數實現批量梯度下降。

# This function learns parameters for the neural network and returns the model.

# - nn_hdim: Number of nodes in the hidden layer

# - num_passes: Number of passes through the training data for gradient descent

# - print_loss: If True, print the loss every 1000 iterations

def build_model(nn_hdim, num_passes=20000, print_loss=False):

     

    # Initialize the parameters to random values. We need to learn these.

    np.random.seed(0)

    W1 = np.random.randn(nn_input_dim, nn_hdim) / np.sqrt(nn_input_dim)

    b1 = np.zeros((1, nn_hdim))

    W2 = np.random.randn(nn_hdim, nn_output_dim) / np.sqrt(nn_hdim)

    b2 = np.zeros((1, nn_output_dim))


    # This is what we return at the end

    model = {}

     

    # Gradient descent. For each batch...

    for i in xrange(0, num_passes):


        # Forward propagation

        z1 = X.dot(W1) + b1

        a1 = np.tanh(z1)

        z2 = a1.dot(W2) + b2

        exp_scores = np.exp(z2)

        probs = exp_scores / np.sum(exp_scores, axis=1, keepdims=True)


        # Backpropagation

        delta3 = probs

        delta3[range(num_examples), y] -= 1

        dW2 = (a1.T).dot(delta3)

        db2 = np.sum(delta3, axis=0, keepdims=True)

        delta2 = delta3.dot(W2.T) * (1 - np.power(a1, 2))

        dW1 = np.dot(X.T, delta2)

        db1 = np.sum(delta2, axis=0)


        # Add regularization terms (b1 and b2 don't have regularization terms)

        dW2 += reg_lambda * W2

        dW1 += reg_lambda * W1


        # Gradient descent parameter update

        W1 += -epsilon * dW1

        b1 += -epsilon * db1

        W2 += -epsilon * dW2

        b2 += -epsilon * db2

         

        # Assign new parameters to the model

        model = { 'W1': W1, 'b1': b1, 'W2': W2, 'b2': b2}

         

        # Optionally print the loss.

        # This is expensive because it uses the whole dataset, so we don't want to do it too often.

        if print_loss and i % 1000 == 0:

          print "Loss after iteration %i: %f" %(i, calculate_loss(model))

     

    return model

具有大小為3的隱藏層的網路

讓我們看看如果我們訓練隱藏層大小為3的網路會發生什麼。

# Build a model with a 3-dimensional hidden layer

model = build_model(3, print_loss=True)


# Plot the decision boundary

plot_decision_boundary(lambda x: predict(model, x))

plt.title("Decision Boundary for hidden layer size 3")

好極了！這看起來很不錯。我們的神經網路能夠找到一個成功分離類的決策邊界。

改變隱藏的圖層大小

在上面的示例中，我們選擇了隱藏的圖層大小3.讓我們現在瞭解隱藏圖層大小的變化如何影響結果。

plt.figure(figsize=(16, 32))

hidden_layer_dimensions = [1, 2, 3, 4, 5, 20, 50]

for i, nn_hdim in enumerate(hidden_layer_dimensions):

    plt.subplot(5, 2, i+1)

    plt.title('Hidden Layer size %d' % nn_hdim)

    model = build_model(nn_hdim)

    plot_decision_boundary(lambda x: predict(model, x))

plt.show()

我們可以看到隱藏的低維度層很好地捕捉了我們資料的總體趨勢。較高的尺寸易於過度擬合。它們“記憶”資料而不是擬合一般形狀。如果我們在一個單獨的測試集上評估我們的模型（你應該！），由於更好的泛化，具有較小隱藏層大小的模型可能會表現得更好。我們可以用更強的正則化來抵消過度擬合，但為隱藏層選擇正確的尺寸是一種更“經濟”的解決方案

練習 

以下是您可以嘗試更熟悉程式碼的一些事項：

1、使用minibatch梯度下降（更多資訊），而不是批量梯度下降，來訓練網路。 Minibatch梯度下降通常在實踐中表現更好。

2、我們使用固定學習率進行梯度下降。實現梯度下降學習率的退火計劃（更多資訊）。

3、我們為隱藏層使用了tanh啟用函式。嘗試其他啟用功能（一些在上面提到）。請注意，更改啟用功能還意味著更改反向傳播導數。

4、將網路從兩個類擴充套件到三個類。您需要為此生成適當的資料集。

5、將網路擴充套件到四層。試驗圖層大小。新增另一個隱藏層意味著您需要調整前向傳播和後向傳播程式碼。