這是Python之禪和他朋友們在知識星球的第4題：用Python實現斐波那契數列

斐波那契數列（Fibonacci）最早由印度數學家Gopala提出，而第一個真正研究斐波那契數列的是義大利數學家 Leonardo Fibonacci，斐波那契數列的定義很簡單，用數學函式可表示為：

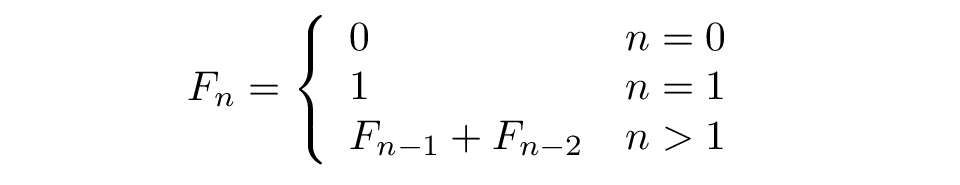
數列從0和1開始，之後的數由前兩個數相加而得出，例如斐波那契數列的前10個數是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34。

用 Python 實現斐波那契數列常見的寫法有三種，各演算法的執行效率也有很大差別，在面試中也會偶爾會被問到，通常面試的時候不是讓你簡單的用遞迴寫寫就完了，還會問你時間複雜度怎樣，空間複雜度怎樣，有沒有可改進的地方。

遞迴法

所謂遞迴就是指函式的定義中使用了函式自身的方法

def fib_recur(n):
    assert n >= 0
    if n in (0, 1):
        return n
    return fib_recur(n - 1) + fib_recur(n - 2)

for i in range(20):
    print(fib_recur(i), end=" ")

>>> 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 

遞迴是一種程式碼最簡潔的方法，但它是效率非常低，因為會出現大量的重複計算，時間複雜度是：O(1.618 ^ n)，1.618是黃金分割。同時受限於 Python 中遞迴的最大深度是 1000，所以用遞迴來求解並不是一種可取的辦法。

遞推法

遞推法就是從0和1開始，前兩項相加逐個求出第3、第4個數，直到求出第n個數的值

def fib_loop(n):
    a, b = 0, 1
    for i in range(n):
        a, b = b, a + b
    return a

for i in range(20):
    print(fib_loop(i), end=" ")

>>> 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 

這種演算法的時間複雜是O(n)，呈線性增長，如果資料量巨大，速度越到後面會越慢。

上面兩種方式都是使用分而治之的思想，就是把一個大的問題化小，然後利用小問題的求解得到目標問題的答案。

矩陣法

《線性代數》是大學計算機專業低年級的課程，這門課教的就是矩陣，那時候覺得這東西學起來很枯燥，沒什麼用處，工作後你才發現搞機器學習、資料分析、資料建模時大有用處，書到用時方恨少。其實矩陣的本質就是線性方程式。

斐波那契數列中兩個相鄰的項分別為：F(n) 和 F(n - 1)，如果把這兩個數當作一個2行1列的矩陣可表示為：

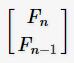
因為 F(n) = F(n-1)+F(n-2)，所以就有：

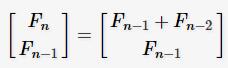
通過反推，其實它是兩個矩陣的乘積得來的

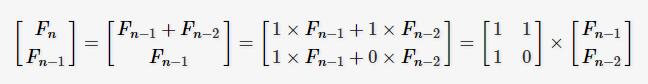
依此類推：

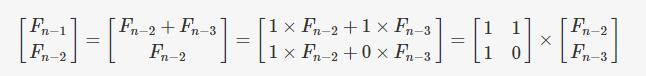
最後可推出：

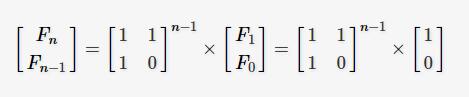
因此想要求出F(n)的值，只要能求出右邊矩陣的n-1次方的值，最後求得兩矩陣乘積，取新矩陣的第一行的第一列的值即可，比如n=3時，

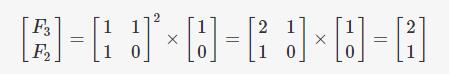
​可以得知F(3)的值2，F(2)的值為1，因為冪運算可以使用二分加速，所以矩陣法的時間複雜度為 O(log n)

我們可以用科學計算包 numpy 來實現矩陣法：

import numpy

def fib_matr(n):
    return (numpy.matrix([[1, 1], [1, 0]]) ** (n - 1) * numpy.matrix([[1], [0]]))[0, 0]

for i in range(20):
    print(int(fib_matr(i)), end=" ")

>>> 0 1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987 1597 2584 4181 

3中不同的演算法效率對比：

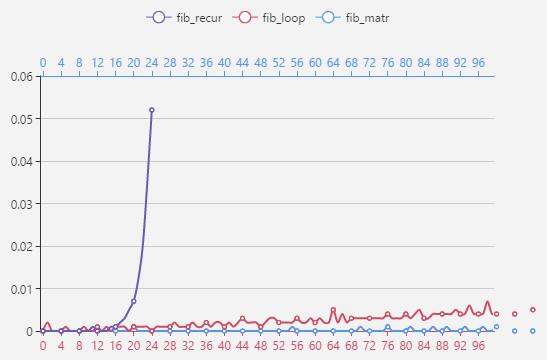
從上面圖可以看出遞迴法效率驚人的低，矩陣法在資料量比較大的時候才突顯出它的優勢，遞推法隨著資料的變大，所花的時間也越來越大。

參考連結：

• https://www.ted.com/talks/arthur_benjamin_the_magic_of_fibonacci_numbers?language=zh-cn#t-364274
• https://www.zhihu.com/question/28062458
• https://www.nayuki.io/page/fast-fibonacci-algorithms
• http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html

關注公眾號「Python之禪」（id：vttalk）獲取最新文章