題目

In this problem, a rooted tree is a directed graph such that, there is exactly one node (the root) for which all other nodes are descendants of this node, plus every node has exactly one parent, except for the root node which has no parents.

The given input is a directed graph that started as a rooted tree with N nodes (with distinct values 1, 2, …, N), with one additional directed edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.

The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] that represents a directed edge connecting nodes u and v, where u is a parent of child v.

Return an edge that can be removed so that the resulting graph is a rooted tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array.

Example 1:

Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given directed graph will be like this:
  1
 / \
v   v
2-->3

Example 2:

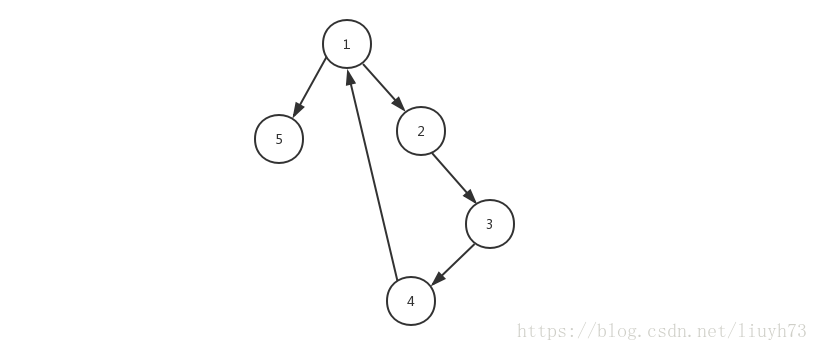
Input: [[1,2], [2,3], [3,4], [4,1], [1,5]]
Output: [4,1]
Explanation: The given directed graph will be like this:
5 <- 1 -> 2
     ^    |
     |    v
 

     4 <- 3

Note: The size of the input 2D-array will be between 3 and 1000. Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.

思路與解法

這道題目與684. Redundant Connection題目大致相同，都是從原圖中刪除一條邊，使得原圖轉化為一顆樹，所以輸入的圖一定是連通圖。不過，該圖中的樹邊為有向邊。所以，原來的思路不能夠直接照搬下來，而要做一些調整。 首先，我們可以大致將輸入資料分為如下兩種情況：

1. 所有節點的入度都為1
2. 存在某個節點的入度為2 以上兩種情況便包含了輸入資料的所有可能，因為不可能存在某個節點的入度大於2的情況。如果入度大於2，則說明該節點存在三個父親節點（可能相同），刪除一條邊之後，該節點仍然還有兩個父親節點，則不滿足題目條件，無法構成一顆有向樹。 對於第一個圖中所描述的情況，我們仍然可以用並查集的思想來進行判別，程式碼與684. Redundant Connection方法二相同，不在詳細介紹。 對於第二個圖中所描述的情況，我們可以任意去掉入度為2的節點的一條入邊，假設為edge，然後從某個入度為0的節點利用BFS遍歷該有向圖，如果所有節點被訪問了一次，則證明刪除掉edge後，形成了一顆有向樹；否則，如果BFS結束後存在某些節點沒有被訪問到，則剩餘節點形成了環，說明刪除edge並沒有形成有向樹，此時應該刪除另外一條入邊。

程式碼實現

此演算法我才用go語言實現：

func findRedundantDirectedConnection(edges [][]int) []int {
   /*
    * graph 儲存反向圖（類似於鄰接矩陣），用於獲得入度為2的節點的其中1條入邊，另外一條在輸入時進行儲存
    * graph 儲存正向圖（類似於鄰接表），用於遍歷該圖
    * node_count 儲存節點數（等於邊數）
    * in_degree 統計每個節點入度
    * double_in_degree 儲存入度為2的節點
    * candidate 儲存候選的邊（用於刪除），即為入度為2的節點的其中1條入邊
    */
    graph := make(map[int]int)
    graph2 := make(map[int][]int)
    nodes_count := len(edges)
    in_degree := make([]int, nodes_count+1)
    double_in_degree := -1
    candidate := -1
    /* 初始化graph和graph2，統計入度，並且獲得double_in_degree和candidate */
    for _, edge := range edges {
        if in_degree[edge[1]] > 0 {
            double_in_degree = edge[1]
            candidate = edge[0]
        } else {
            graph2[edge[0]] = append(graph2[edge[0]], edge[1])
            graph[edge[1]] = edge[0]
            in_degree[edge[1]]++
        }
    }
	/* 對應於第一個圖中的情況 並查集 */
    if double_in_degree == -1 {
        parents := make([]int ,len(edges)+1)
        for _, edge := range edges {
            parent0 := findParent(edge[0], parents)
            parent1 := findParent(edge[1], parents)

            if parent0 == parent1 {
                return edge
            }
            parents[parent1] = parent0
        }
    } else {
        /* 對應於第二個圖中的情況 BFS便利圖*/
        queue := make([]int, 0)
        visited := make([]int, 0)
		
        for i:=1; i<=nodes_count; i++ {
            if in_degree[i] == 0 {
                queue = append(queue, i)
                visited = append(visited, i)
            }
        }
        /* 如果存在2個及以上的入度為0的節點，則candidate並不滿足題目要求（因為即使刪除該邊，也不能形成一個有向樹） */
        if len(queue) > 1 {
            return []int{graph[double_in_degree], double_in_degree}
        }

        for len(queue)!=0 {
            head := queue[0]
            queue = queue[1:]
            for _, next := range graph2[head] {
                in_degree[next]--
                if in_degree[next] ==0 {
                    queue = append(queue, next)
                    visited = append(visited, next)
                }
            }
        }
        /* 遍歷完整個圖，形成一棵有向樹 */
        if len(visited) == nodes_count {
            return []int{candidate, double_in_degree}
        }
        return []int{graph[double_in_degree], double_in_degree}
    }
    return []int{}
}

func findParent(node int, parents []int) int {
    if parents[node] == 0 {
        return node
    }
    return findParent(parents[node], parents)
}

評測結果

從上圖可以看出，程式碼的執行效率還是很高的。但是，由於整個圖儲存了兩遍，所以所耗費的空間有些多，希望以後可以進行改進。