線性排序演算法

計數排序

假設：有n個數的集合，而且n個數的範圍都在0~k(k = O(n))之間。

執行時間：Θ(n+k)

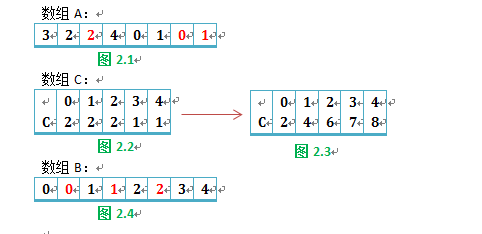
待排序陣列A如圖2.1所示，需要輔助陣列B(儲存最後排序結果)，陣列C(儲存元素的個數)。基於上述的假設，陣列C的大小為k，C[i]表示陣列A中元素i(0 <= i < k)的個數(如圖2.2所示)，為了保證計數排序的穩定性，陣列C變化為圖2.3，C[i]表示小於或者等於i的個數。程式碼如下：

   1: /*

   2:     輸入：待排序陣列A,儲存排序後的陣列B，陣列A的大小，陣列C的大小

   3:     功能：計數排序

   4: */

   5: void CountingSort(int A[], int B[], int len, int k)
 

   6: {

   7:     int *CountArr = new int[k];

   8:     int i;

   9:     for (i = 0; i < k; i++)

  10:     {

  11:         CountArr[i] = 0;

  12:     }

  13:  

  14:     for (i = 0; i < len; i++)

  15:     {

  16:         CountArr[A[i]]++;                

  17:     }

  18:  

  19:     for (i = 1; i < k; i++)
 

  20:     {

  21:         CountArr[i] += CountArr[i-1];

  22:     }

  23:  

  24:     // 從右至左保證演算法的穩定性

  25:     for (i = len-1; i >=0; i--)

  26:     {

  27:         B[CountArr[A[i]]-1] = A[i];

  28:         CountArr[A[i]]--;

  29:     }

  30: }

9-12行和19-22行的執行時間Θ(k)，14-17行和25-29行的執行時間為Θ(n)，所以總的執行時間為Θ(2(n+k)) = Θ(n+k)。

基數排序

基數排序：將所有待比較數值(正整數)統一為同樣的數位長度，數位較短的數前面補零。然後，從最低位開始，依次進行一次排序。這樣從最低位排序一直到最高位排序完成以後， 數列就變成一個有序序列。

基數排序分為兩種LSD和MSD。

LSD(Least significant digital)：最低有效位優先，即從右向左開始排序。

MSD(Most significant digital)：最高有效位優先，即從左往右開始排序。

以下是LSD方式的基數排序的虛擬碼

   1: RadixSort(A,d)

   2:     for i <- 1 to d

   3:         用穩定的排序演算法排列陣列A中元素的第i位

如圖3：先牌個位，然後十位，最後百位。為陣列的某一位排序的時候一定需要穩定的演算法。

執行時間為Θ(d(n+k))。在基數排序中排列陣列各位的演算法是計數排序所以執行時間為Θ(n+k)，又d是陣列中數的最大位數。

桶排序

桶排序：將陣列分到有限個桶子內，然後再對桶子裡面的序列進行排序，執行時間Θ(n)。桶排序基於一個假設：輸入的資料由隨機過程構成，否則在最壞情況下都分配到一個桶子裡面，如果又不滿足計數排序的假設要求，那麼只能使用基於比較的排序演算法進行排序，執行時間就退化到Ω(nlogn)。

排序演算法穩定性

排序演算法穩定性：假設待排序序列中有兩個元素相等，而且在排序前和排序後兩個相等的元素的相對位置不變，即有 a = b，排序前a在b前面，那麼排序後，a還是要在b前面。排序演算法的穩定性是要看具體的演算法實現，比如一般情況下，直接選擇排序，快速排序，希爾排序，堆排序都不是穩定排序演算法，基數排序，計數排序，歸併排序，插入排序，氣泡排序都是穩定排序演算法。

快速排序：A = {2， 2， 1}，排序後A = {1，2，2}。

希爾排序：A = {1，2，5，4，4，7}，排序後（k = 2）；A = {1， 2， 4， 4， 5， 7} 。

堆排序：A = {2，2，1}，排序後A = {1，2， 2}。

直接選擇排序： A = {4， 4， 2， 5},排序後 A = {2，4， 4， 5}。

以上舉例都不滿足穩定性。