迴圈神經網路(Recurrent Neural Network, RNN)
1. 前向傳播
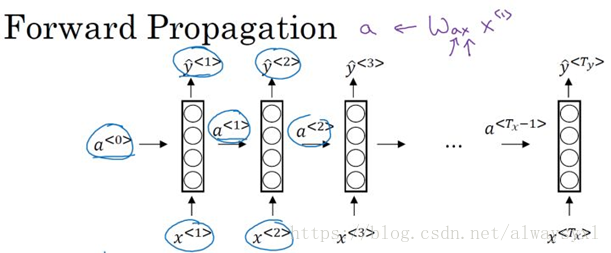
Note
- 一般而言,初始啟用向量為:a<0>=0
- 通常,g(a)選擇tanh函式(tanh函式梯度消失的問題會用其他方式解決),有時也會選用relu函式。
- y^<t>=g(y)(Wyaa<t>+by)如果是二分類問題,使用sigmoid函式,如果是多分類問題,可以使用softmax函式。
2. 損失函式
為了進行反向傳播計算,使用梯度下降等方法來更新RNN的引數,我們需要定義一個損失函式,如下: L(y^,y)=∑t=1TyL<t>(y^<t>,y<t>)=∑t=1Ty−(y<t>log(y^<t>)+(1−y<t>)log(1−y^<t>))
3. BPTT
RNN的反向傳播將在後續部分有專門的介紹。
相關推薦
迴圈神經網路(Recurrent Neural Network, RNN)
1. 前向傳播 at=g(a)(Waaa<t−1>+Waxx<t>+ba)a^{t}=g^{(a)}(W_{aa}a^{<t-1>}+W_{ax}x^{<t&a
DeepLearning.ai作業:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)(1)
title: ‘DeepLearning.ai作業:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)(1)’ id: dl-ai-5-1h1 tags: dl.ai homework categories: AI Deep
DeepLearning.ai筆記:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)
title: ‘DeepLearning.ai筆記:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)’ id: dl-ai-5-1 tags: dl.ai categories: AI Deep Learning date: 2
DeepLearning.ai作業:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)(2)
title: ‘DeepLearning.ai作業:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)(2)’ id: dl-ai-5-1h2 tags: dl.ai homework categories: AI Deep
DeepLearning.ai作業:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)(3)
title: ‘DeepLearning.ai作業:(5-1)-- 迴圈神經網路(Recurrent Neural Networks)(3)’ id: dl-ai-5-1h3 tags: dl.ai homework categories: AI Deep
深度神經網路(Deep Neural Network)
dZ[l]=dA[l]∗g[l]′(Z[l])dW[l]=1mdZ[l]⋅A[l−1]db[l]=1mnp.sum(dZ[l],axis=1,keepdims=True)dA[l−1]=W[l]T⋅dZ[l]
從迴圈神經網路(RNN)到LSTM網路
通常,資料的存在形式有語音、文字、影象、視訊等。因為我的研究方向主要是影象識別,所以很少用有“記憶性”的深度網路。懷著對迴圈神經網路的興趣,在看懂了有關它的理論後,我又看了Github上提供的tensorflow實現,覺得收穫很大,故在這裡把我的理解記錄下來,也希望對大家能有所幫助。
基於PTB資料集實現RNN-LSTM迴圈神經網路(智慧填詞)
本篇直入主題,做一篇學習的記錄,在學習RNN的時候,跟著教程敲了一個案例 分為處理方法檔案,神經網路模型檔案,訓練方法檔案,測試檔案 所有的操作和重要內容都在程式碼中作了詳細的註釋 一、目標神經網路模型 二、資料集 PT
迴圈神經網路(RNN)原理通俗解釋
1.RNN怎麼來的? 2.RNN的網路結構及原理 3.RNN的改進1:雙向RNN 4.RNN的改進2:深層雙向RNN 4.1 Pyramidal RNN
序列模型(5)-----雙向神經網路(BRNN)和深層迴圈神經網路(Deep RNN)
一、雙向迴圈神經網路BRNN 採用BRNN原因: 雙向RNN,即可以從過去的時間點獲取記憶,又可以從未來的時間點獲取資訊。為什麼要獲取未來的資訊呢? 判斷下面句子中Teddy是否是人名,如果只從前面兩個詞是無法得知Teddy是否是人名,如果能有後面的資訊就很好判斷了,這就需要用的雙向迴圈神經網路。
吳恩達序列模型學習筆記--迴圈神經網路(RNN)
1. 序列模型的應用 序列模型能解決哪些激動人心的問題呢? 語音識別:將輸入的語音訊號直接輸出相應的語音文字資訊。無論是語音訊號還是文字資訊均是序列資料。 音樂生成:生成音樂樂譜。只有輸出的音樂樂譜是序列資料,輸入可以是空或者一個整數。 情感分類:將輸入的評論句子轉換
迴圈神經網路(一般RNN)推導
本文章的例子來自於WILDML vanillaRNN是相比於LSTMs和GRUs簡單的迴圈神經網路,可以說是最簡單的RNN。 RNN結構 RNN的一個特點是所有的隱層共享引數(U,V,W),整個網路只用這一套引數。 RNN前向傳導 st=tan
對迴圈神經網路(RNN)中time step的理解
微信公眾號 1. 傳統的迴圈神經網路 傳統的神經網路可以看作只有兩個time step。如果輸入是“Hello”(第一個time step),它會預測“World”(第二個time step),但是它無法預測更多的time step。
迴圈神經網路(RNN)
1.NN & RNN 在神經網路從原理到實現一文中已經比較詳細地介紹了神經網路,下面用一張圖直觀地比較NN與RNN地不同。從圖1中可以看出,RNN比NN多了指向自己的環,即圖1中的7,8,9,
04-迴圈神經網路(RNN)和LSTM
RNN(Recurrent NeuralNetwork)和LSTM(Long Short Term Memory)RNN(Recurrent NeuralNetwork)RNN:存在隨著時間的流逝,訊號會不斷的衰弱(梯度消失)LSTM(Long Short Term Memo
深度學習【8】基於迴圈神經網路(RNN)的端到端(end-to-end)對話系統
注:本篇部落格主要內容來自:A Neural Conversational Model,這篇論文。 http://blog.csdn.net/linmingan/article/details/51077837 與傳統的基於資料庫匹配的對話\翻譯系統不一樣
大話迴圈神經網路(RNN)
—— 原文釋出於本人的微信公眾號“大資料與人工智慧Lab”(BigdataAILab),歡迎關注。 卷積神經網路CNN在影象識別中有著強大、廣泛的應用,但有一些場景用CNN卻無法得到有效地解決,例如:語音識別,要按順序處理每一幀的聲音資訊,有些結果需要根據上下文進行識別;自然
深度學習:迴圈神經網路(RNN)的變體LSTM、GRU
訪問請移步至,這裡有能“擊穿”平行宇宙的亂序並行位元組流… 假設我們試著去預測“I grew up in France… I speak fluent French”最後的詞French。當前的資訊建議下一個詞可能是一種語言的名字,但是如果我們需要弄清楚是什麼
機器學習之迴圈神經網路(十)
摘要: 多層反饋RNN(Recurrent neural Network、迴圈神經網路)神經網路是一種節點定向連線成環的人工神經網路。這種網路的內部狀態可以展示動態時序行為。不同於前饋神經網路的是,RNN可以利用它內部的記憶來處理任意時序的輸入序列,這讓
DeepLearning.ai筆記:(1-4)-- 深層神經網路(Deep neural networks)
這一週主要講了深層的神經網路搭建。 深層神經網路的符號表示 在深層的神經網路中, LL表示神經網路的層數 L=4L=4 n[l]n[l]表示第ll層的神經網路個數 W[l]:(n[l],nl−1)W[l]:(n[l],nl−1) dW[l
