參考文獻： http://blog.sina.com.cn/s/blog_ac7218750101giyf.html

https://blog.csdn.net/saltriver/article/details/80547245

https://ww2.mathworks.cn/help/images/ref/hough.html

霍夫變換

霍夫變換是1972年提出來的，最開始就是用來在影象中過檢測直線，後來擴充套件能檢測圓、曲線等。

直線的霍夫變換就是 把xy空間的直線 換成成 另一空間的點。就是直線和點的互換。

我們在初中數學中瞭解到，一條直線可以用如下的方程來表示：y=kx+b，k是直線的斜率，

我們轉換下變成：b=-kx+y。我們是不是也可以把（k，b）看作另外一個空間中的點？這就是k-b引數空間。 這樣，我們就把一條x-y直線用一個（k，b）的點表示出來了。

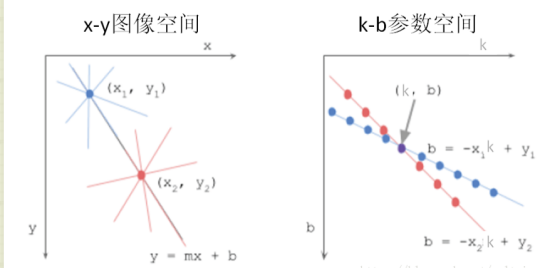
我們看到，在x-y影象空間中的一個點，變成了k-b引數空間中的一條直線，而x-y影象空間中的2點連成的直線，變成了k-b引數空間中的一個交點。

如果x-y影象空間中有很多點在k-b空間中相交於一點，那麼這個交點就是我們要檢測的直線。這就是霍夫變換檢測直線的基本原理。

當然，有一個問題需要注意，影象空間中如果一條直線是垂直的，那麼斜率k是沒有定義的（或者說無窮大）。為了避免這個問題，霍夫變換採用了另一個引數空間：距離

我們在中學中學過，平面上的一個點也可以用距離-角度來定義，也就是極座標。那麼在影象中，每一個點都可以用距離和角度來表達：

但是，使用距離-角度後，點（x，y）與距離，角度的關係變成了：

ρ=xcosθ+ysinθ

於是，在新的距離-角度引數空間中，影象中的一個點變成了一個正弦曲線，而不是k-b引數空間中的直線了。這些正弦曲線的交點就是影象空間中我們要檢測的直線了。

Matlab霍夫變換的函式詳解

[H, theta, rho] = hough(BW,ParameterName, ParameterValue)

BW：二值圖

ParameterName：'RhoResolution'或'Theta'

RhoResolution-指定在累計陣列中（檢測極值）的檢測間隔？預設為1

Theta-指定檢測的角度範圍（不超過-90~90度）以及間隔，例如-90:0.5:89.5，預設-90:1:89

H：累計陣列

Theta：H對應的θ，實際上H的大小就是Rho×Theta

Rho：H對應的ρ

 這兩個引數值的注意，RhoResolution太大覆蓋不到極值點，檢測到一些不對應直線的次極值，

峰值提取

peaks = houghpeaks(H,numpeaks)

peaks = houghpeaks(...,param1, val1, param2, val2)

H：累計陣列；

Numpeaks：指定需要檢測的峰值個數；

Param1：可以是'Threshold'或'NHoodSize'

'Threshold'-指定峰值的域值，預設是0.5*max(H(:))

'NHoodSize'-是個二維向量[m,n]，檢測到一個峰值後，將峰值周圍[m,n]內元素置零。

畫直線段

lines = houghlines(BW,theta, rho, peaks)

lines = houghlines(...,param1, val1, param2, val2)

BW：二值圖

Theta、rho、peaks：分別來自函式hough和houghpeaks

Lines：結構陣列，大小等於檢測到的直線段數，每個單元包含

Point1、point2：線段的端點

Theta、rho：線段的theta和rho

待續。。。。