該部落格所需程式碼和資原始檔可以到Github中進行下載。

霍夫變換本質上是座標變換，如下圖1，左半部分表示直線的xy空間，直線方程為$y=mx+c$，其中斜率為m，截距為c。右半部分表示將直線從xy空間變換到mc空間，取直線在xy空間上的四點1,2,3,4，在mc空間就是不同斜率和截距的四條直線。

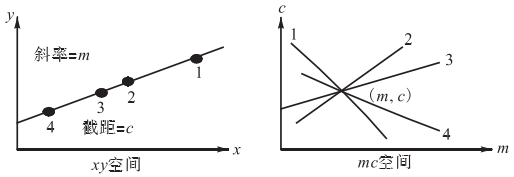
圖1 直線座標系變換

那麼，在mc空間中四條直線的交點處的m值和c值就對應xy空間中直線的m和c。同理，對圖片中的直線來說，將直線中的每個點都變換到變換後空間，找出多條直線相交的點就可以找出變換前空間的直線。

圖1是為了更好理解座標變換的概念，但是在實際應用中是將xy空間變換到極座標系，方程為$\rho$

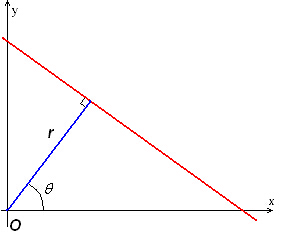
圖2 直線的極座標系引數

其中r，即$\rho$為原點到直線的垂直距離，$\theta$為與x軸的夾角。從上述極座標方程可以看出，將該直線變換到$\rho\theta$座標系後將是一系列不同初相、幅度，但是週期均為$2\pi$的正弦曲線，所有正弦曲線交點處的$\rho和\theta$將代表xy空間中的這條直線。

下圖3為測試影象，是一張簡單但是有代表性的影象。

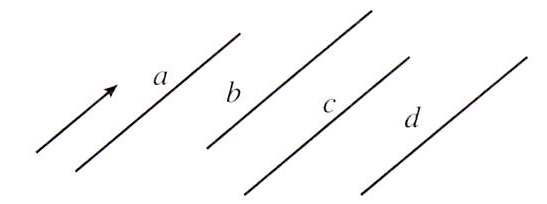
圖3 測試影象

以下程式碼先根據canny運算元找出圖片的邊緣，將圖片邊緣經過霍夫變換，變換到$\rho$

img  = imread('line.jpg');
subplot(221), imshow(img), title('original image');
img_gray = rgb2gray(img);
% the canny edge of image
BW = edge(img_gray,'canny');
subplot(223), imshow(BW), title('image edge');
% the theta and rho of transformed space
[H,Theta,Rho] = hough(BW);
subplot(222), imshow(H,[],'XData',Theta,'YData',Rho,'InitialMagnification','fit'),...
    title('rho\_theta space and peaks');
xlabel('\theta'), ylabel('\rho');
axis on, axis normal, hold on;
% label the top 5 intersections
P  = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
x = Theta(P(:,2)); 
y = Rho(P(:,1));
plot(x,y,'*','color','r');
 

邊緣資訊和相應的霍夫變換結果如下圖4。

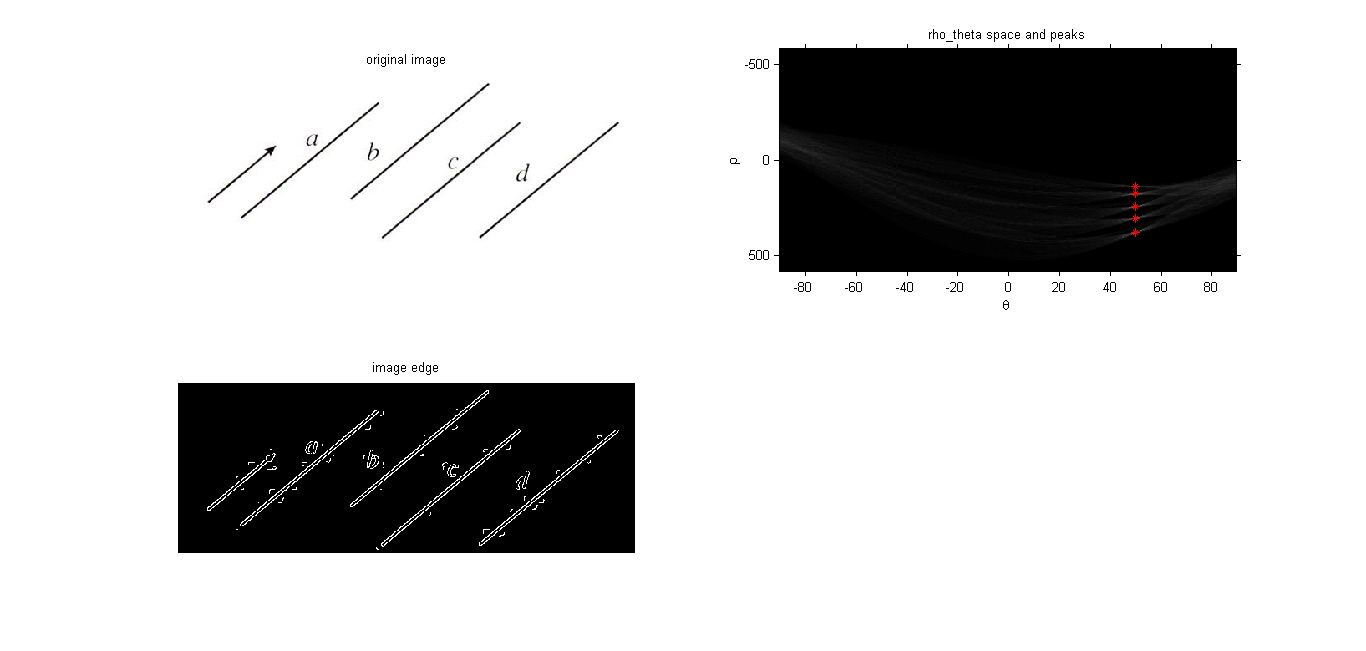
圖4 霍夫變換結果

上述程式碼找到了5條直線對應的$\rho和\theta$，通過如下程式碼進行反變換在原圖中標記出相應的直線。

% find lines and plot them
lines = houghlines(BW,Theta,Rho,P,'FillGap',5,'MinLength',7);
figure, imshow(img), hold on
max_len = 0;
for k = 1:length(lines)
 xy = [lines(k).point1; lines(k).point2];
 plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','r');
end

最終結果如下圖5。

圖5 霍夫變換最終結果

參考網址