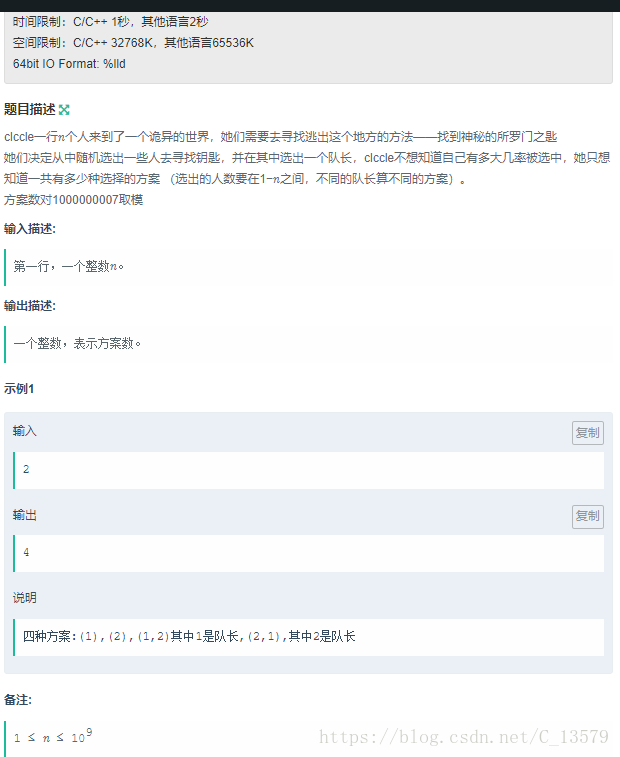
思路：題目公式為 ans=C(1,n)*1+C(2,n)*2+...+C(n-1,n)*(n-1)+C(n,n)*n

ans-n=C(1,n)*1+C(2,n)*2+...+C(n-1,n)*(n-1)

將右邊反向相加得 2*(ans-n)=(C(1,n)*1+C(n-1,n)*(n-1))+(C(2,n)*2+C(n-2,n)*(n-2)+...+(C(n-1,n)*(n-1)+C(1,n)*n)

又C(k,n)=C(n-k,n)

則 2*(ans-n)=C(1,n)*n+C(2,n)*n+...+C(n-1,n)*n=n*(C(1,n)+C(2,n)+...+C(n-1,n))

而C(1,n)+C(2,n)+...+C(n-1,n)+C(n,n)=(2^n)-1

C(1,n)+C(2,n)+...+C(n-1,n)=(2^n)-2;

則 2*(ans-n)=n*((2^n)-2)=n*(2^n)-2*n

所以 ans=n*(2^n)/2=n*(2^(n-1))

Code:

#include<iostream>
using namespace std;
typedef long long LL;

const int MOD=1000000007;
int n;

int main()
{
	ios::sync_with_stdio(false); 
	while(cin>>n){
		LL ans=n--,a=2;
		while(n){
			if(n&1)	ans=ans*a%MOD;
			n>>=1;
			a=a*a%MOD;
		}
		cout<<ans<<endl;
	}
	
	return 0;
}