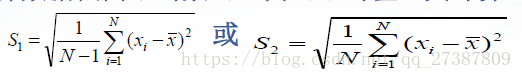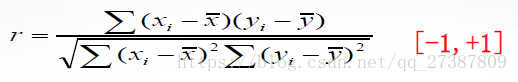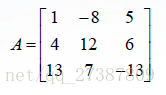MATLAB學習筆記——5.1 資料統計與分析
1、求矩陣的最大元素和最小元素
-
函式: max():求向量或矩陣的最大元素; min():求向量或矩陣的最小元素;
-
當引數為向量時,上述函有兩種呼叫格式: (1)y=max(X):返回向量 : X的最大值存y,如果 X中包含複數元素,則按模取最大值。 (2)[y,k ]=max(X):返回向量 X的最大值存入y,最大值元素的序號存入 k,如果 X中包含複數元素,則按模取最大值。
-
例5.1.1: 求向量x的最大元素,其中x=[-43,72,9,16,23,47]。
x=[-43,72,9,16,23,47];
y=max(x)
[y,k]=max(x)
命令列視窗:
>> x=[-43,72,9,16,23,47]; >> y=max(x) y = 72 >> [y,k]=max(x) y = 72 k = 2
-
當引數為矩陣時,函式有三種呼叫形式: (1)max(A):返回一個行向量,的第i個元素是矩陣A的第i列上的最大值。 (2)[Y,U]=max(A):返回行向量Y和U,Y向量記錄A中每列的最大值,U向量記錄每列最大值元素的行號。 (3)max(A,[],dim):dim取1或2。dim取1時,該函式的功能和max(A)完全相同;dim取2時,該函式返回一個列向量其第i個元素是A矩陣的第i行上的最大值。
-
思考:對矩陣按行求最大元素,僅使用第一種格式能夠做到嗎?
-
想法:連續使用兩次max()函式就能實現,第一次對矩陣A使用,返回每個列的最大值組成的向量,接著對這個陣列使用該函式,最後返回矩陣的最大值。(max(max(A)))
-
例5.1.2: 求矩陣A的每行及每列的最大元素,並求整個矩陣的最大元素。
A=[13,-56,78;25,63,-235;78,25,563;1,0,-1];
max(A)
max(A,[],2)
max(max(A))
命令列視窗:
>> A=[13,-56,78;25,63,-235;78,25,563;1,0,-1]; >> max(A) ans = 78 63 563 >> max(A,[],2) ans = 78 63 563 1 >> max(max(A)) ans = 563
- 思考:用什麼方法只調用一次max函式就能求得整個矩陣的最大值?
- 想法:先將A中所有元素堆疊成列向量,然後只需要使用一次max函式
max(A(:)
2、求矩陣的平均值 和中求矩陣的平均值 和中求矩陣的平均值 和中求矩陣的平均值
- 平均值:指算術,即每項資料之和除以。
- 中值:指在資料序列其的大小恰好處間元素。如果個為奇數,則取值為大小位於中間的元素;如果據個偶兩素的平均值。
- 在MATLAB 中,求平均值和的函式分別為: mean() :求算術平均值。 median() :求中值。
- 思考:有了平均值,為什麼還要中值?
- 想法:中值與平均值未必相等。
- 例5.1.3: 某學生宿舍的5位同學月生活費如向量x所示,其中,小明同學家境一般,請問他應該按什麼標準向父母主張生活費額度才較為合理。x=[1200,800,1500,1000,5000]
x=[1200,800,1500,1000,5000];
mean(x)
median(x)
執行結果:
>> x=[1200,800,1500,1000,5000];
>> mean(x)
ans =
1900
>> median(x)
ans =
1200
3、求和與求積
- sum():求和函式。
- prod():求積函式。
4、 累加和與累乘積
設U=(u1,u2,…,un)是一個向量,V、W是與U等長的另外兩個向量,並且
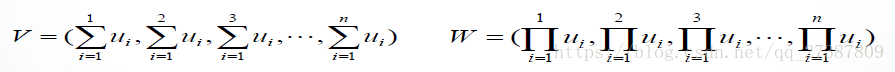
- cumsum():累加和函式。
- cumprod():累乘積函式。
- 例5.1.4 求向量X=[1,2,3,4,5,6,7,8,9,10]的積與累乘積。
>> X=[1,2,3,4,5,6,7,8,9,10];
>> y1=prod(X)
y1=
3628800
>> y2=cumprod(X)
y2=
y2 =
1 2 6 24 120 720 5040 40320 362880 3628800
5. 標準差與相關係數
- 標準差用於計算資料偏離平均數的距離的平均值,其計算公式為
- MATLAB中計算標準差的函式為std(),其呼叫格式為: (1)std(X):計算向量X的標準差。 (2)std(A):計算矩陣A的各列的標準差。 (3)std(A,flag,dim): flag取0或1,當flag=0時,按S1所列公式計算樣本標準方差;當flag=1時,按S2所列公式計算總體標準方差。在預設情況下,flag=0,dim=1。
- 例5.1.5 生成滿足正態分佈的50000*4隨機矩陣,用不同的形式求其各列之間的標準差。
>> x=randn(50000,4);
>> y1=std(x,0,1)
y1 =
0.9955 0.9979 1.0046 0.9990
>> y2=std(x,1,1)
y2 =
0.9955 0.9979 1.0046 0.9990
>> x1=x';
>> y3=std(x1,0,2);
>> y3'
ans =
0.9955 0.9979 1.0046 0.9990
>> y4=std(x1,1,2);
>> y4'
ans =
0.9955 0.9979 1.0046 0.9990
- 相關係數能夠反映兩組資料序列之間相互關係,其計算公式為
- 在MATLAB中,計算相關係數的函式為corrcoef(),其呼叫格式為: (1)corrcoef(A):返回由矩陣A所形成的一個相關係數矩陣,其中,第i行第j列的元素表示原矩陣A中第i列和第j列的相關係數。 (2)corrcoef(X,Y):在這裡,X,Y是向量,它們與corrcoef([X,Y])的作用一 樣,用於求X、Y向量之間的相關係數。
- 例5.1.6
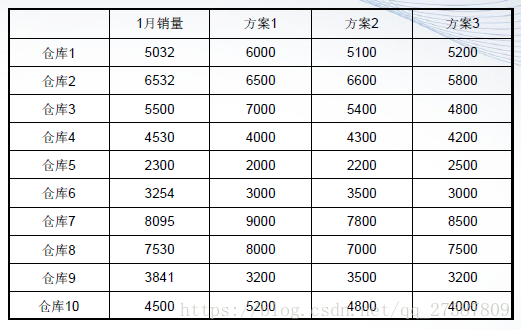
某新產品上市,在上市之前,公司物流部門把新產品分配到不同地區的10個倉庫進行銷售。產品上市一個月後,公司要對各種不同的分配方案進行評估,以便在下一次新產品上市時進行更準確的分配,避免由於分配不當而產生的積壓和斷貨。下表(見課件)是相關資料,請判斷那種分配方案最為合理。
>> A=[5032,6000,5100,5200;6532,6500,6600,5800;
5500,7000,5400,4800;4530,4000,4300,4200;
2300,2000,2200,2500;3254,3000,3500,3000;
8095,9000,7800,8500;7530,8000,7000,7500;
3841,3200,3500,3200;4500,5200,4800,4000];
>> corrcoef(A)
ans =
1.0000 0.9630 0.9906 0.9782
0.9630 1.0000 0.9694 0.9466
0.9906 0.9694 1.0000 0.9635
0.9782 0.9466 0.9635 1.0000
6、 排序
- 在MATLAB 中,排序函式為 sort() ,其呼叫格式為: (1)sort(X) :對向量 X按升序排列。 (2)[Y,I]=sort( A,dim,mode ),其中 dim 指明對 A的列還是行進排序。 mode 指明按升序還是降排,若取“ ascend” ,則按升序;若取“ descend” , 則按降序, 預設為升。輸出引數中Y是排序後的矩陣,而 I記錄 Y中的元素 在A中位置。
- 例5.1.7
對下列矩陣(見課件)做各種排序。
>> A=[1,-8,5;4,12,6;13,7,-13];
>> sort(A)
ans =
1 -8 -13
4 7 5
13 12 6
>> sort(A,2,'descend')
ans =
5 1 -8
12 6 4
13 7 -13
>> [X,I]=sort(A)
X =
1 -8 -13
4 7 5
13 12 6
I =
1 1 3
2 3 1
3 2 2
7、聯絡與討論
7.1 除NaN之外的其他數值元素求和
當向量元素的值暫時無法確定時,可以將其表示為NaN,求向量中除NaN之外的其他數值元素之和。例如A=[1:5, NaN, 10],A中除NaN之外的其他元素之和是25。寫出命令並上機驗證。
- 提示:考慮使用isnan函式,該函式的功能演示如下:
>> A=[1:5, NaN, 10]
A =
1 2 3 4 5 NaN 10
>> isnan(A)
ans =
1×7 logical 陣列
0 0 0 0 0 1 0
解決思路:
Step1 記錄矩陣的size資訊,並將矩陣化為列向量
Step2 通過innan函式找到零元素對應的位置的邏輯陣列
Step3 將Nan資料替換為0(這樣計算時就不影響結果了)
Step4 對向量求和,同時可以將向量恢復成原來的樣子
具體程式碼的實現:
%% Step0 生成隨機維數(0-9)的包含隨機NaN的矩陣a
A=fix(10*rand(fix(1+10*(rand())),fix(1+10*(rand()))));
[m,n]=size(A);
a=A(:);
criterion=1;
while criterion
nannum=round(rand(m*n,1));
nanposi=find(nannum);
criterion=isempty(nanposi);
end
a(nanposi)=NaN;
a=reshape(a,m,n);
disp 'a='
disp (a)
%% Step1 記錄矩陣的size資訊,並將矩陣化為列向量
[m,n]=size(a);
a=a(:);
%% Step2 通過innan函式找到零元素對應的位置的邏輯陣列
b=isnan(a);
%% Step3 將Nan資料替換為0(這樣計算時就不影響結果了)
a(b)=0;
%% Step4 對向量求和,同時可以將向量恢復成原來的樣子
ans1=sum(a);
a=reshape(a,m,n);
disp 'a''='
disp(a)
disp 'ans='
disp(ans1)
7.2 分析函式功能
若A為一個矩陣,試分析函式“max(A,[],2)”和“max(A,2)”各有什麼功能?請上機驗證。 實驗程式碼:
A=magic(5);
ans1=max(A,[],2);
ans2=max(A,2);
disp 'A='
disp(A)
disp 'max(A,[],2)='
disp(ans1)
disp 'max(A,2)='
disp(ans2)
C=max(A,B) returns an array the same size as A and B with the largest elements taken from A or B. The dimensions of A and B must match, or they may be scalar. 返回一個與A和B大小相同的陣列,其中最大元素取自A或B.A和B的維度必須匹配,或者它們可以是標量。
- 對於max(A,[],2)我很清楚,表示尋找A的每行的最大值,並生成列向量,
- 對於max(A,2),看一下執行結果,光看幫助文件還解決不了問題
一個執行結果:
A=
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
max(A,[],2)=
24
23
22
21
25
max(A,2)=
17 24 2 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
好像只有一點點地方不一樣,進一步驗證A與結果的差別
A==ans2
ans =
1 1 0 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
發現只有一個元素和原來不同,這個元素原來是1。 也就是說,
- C=max(A,B):
- 當一個為標量時,對於A中的每一個元素,與B進行比較,取最大值;
- 當都為矩陣,且維度匹配時,對於每一個元素進行比較,取最大值; 驗證:
a=[1 2 3 4 5 6 7 8 9];
b=[9 8 7 6 5 4 3 2 1];
c=max(a,b);
disp(c);
應該得到的結果為: 9 8 7 6 5 6 7 8 9 實際得到的結果為:
9 8 7 6 5 6 7 8 9
符合預期。 再驗證一下b為標量的情況:
a=magic(5);
b=20;
c=max(a,b);
disp(a);
disp(c);
結果為:
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
20 24 20 20 20
23 20 20 20 20
20 20 20 20 22
20 20 20 21 20
20 20 25 20 20
結果符合預期。
7.3 寫出操作命令
利用MATLAB提供的randn函式生成符合正態分佈的10×5隨機矩陣A,進行如下操作: (1)A各列元素的均值和標準方差。 (2)A的最大元素和最小元素。 (3)求A每行元素的和以及全部元素之和。 (4)分別對A的每列元素按升序、每行元素按降序排序。
- 思路:
Step0 生成符合正態分佈的10×5隨機矩陣A
Step1 A各列元素的均值和標準方差
Step2 A的最大元素和最小元素。
Step3 求A每行元素的和以及全部元素之和。
Step4 分別對A的每列元素按升序、每行元素按降序排序。
程式碼的實現:
%% Step0 生成符合正態分佈的10×5隨機矩陣A
A=randn(10,5)
%% Step1 A各列元素的均值和標準方差
mean=mean(A(:))
standard_deviation=std(A(:))
%% Step2 A的最大元素和最小元素。
max=max(A(:))
min=min(A(:))
%% Step3 求A每行元素的和以及全部元素之和。
sum_for_rows=sum(A,2)
sum_for_all=sum(A(:))
%% Step4 分別對A的每列元素按升序、每行元素按降序排序。
sorted=sort(sort(A,1,'ascend'),2,'descend')
- 正態分佈矩陣的生成:randn();