機器學習之聚類(二)
在機器學習和資料探勘中,我們經常需要知道個體間差異的大小,進而評價個體的相似性和類別。最常見的是資料分析中的相關分析,資料探勘中的分類和聚類演算法,如 K 最近鄰(KNN)和 K 均值(K-Means)等等。根據資料特性的不同,可以採用不同的度量方法。一般而言,定義一個距離函式 d(x,y), 需要滿足下面幾個準則:
1) d(x,x) = 0 // 到自己的距離為02) d(x,y) >= 0 // 距離非負3) d(x,y) = d(y,x) // 對稱性: 如果 A 到 B 距離是 a,那麼 B 到 A 的距離也應該是 a4) d(x,k)+ d(k,y) >= d(x,y) // 三角形法則: (兩邊之和大於第三邊)
這篇部落格主要介紹機器學習和資料探勘中一些常見的距離公式,包括:
- 閔可夫斯基距離
- 歐幾里得距離
- 曼哈頓距離
- 切比雪夫距離
- 馬氏距離
- 餘弦相似度
- 皮爾遜相關係數
- 漢明距離
- 傑卡德相似係數
- 編輯距離
- DTW 距離
- KL 散度
1. 閔可夫斯基距離
閔可夫斯基距離(Minkowski distance)是衡量數值點之間距離的一種非常常見的方法,假設數值點 P 和 Q 座標如下:
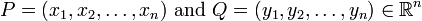
那麼,閔可夫斯基距離定義為:
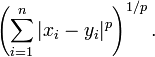
該距離最常用的 p 是 2 和 1, 前者是歐幾里得距離(Euclidean distance),後者是曼哈頓距離(Manhattan distance)。假設在曼哈頓街區乘坐計程車從 P 點到 Q 點,白色表示高樓大廈,灰色表示街道:
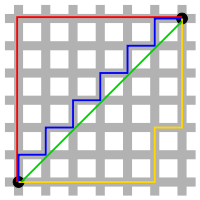
綠色的斜線表示歐幾里得距離,在現實中是不可能的。其他三條折線表示了曼哈頓距離,這三條折線的長度是相等的。
當 p 趨近於無窮大時,閔可夫斯基距離轉化成切比雪夫距離(Chebyshev distance):
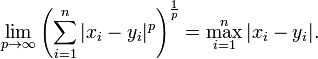
我們知道平面上到原點歐幾里得距離(p = 2)為 1 的點所組成的形狀是一個圓,當 p 取其他數值的時候呢?

注意,當 p < 1 時,閔可夫斯基距離不再符合三角形法則,舉個例子:當 p < 1, (0,0) 到 (1,1) 的距離等於 (1+1)^{1/p} > 2, 而 (0,1) 到這兩個點的距離都是 1。
閔可夫斯基距離比較直觀,但是它與資料的分佈無關,具有一定的侷限性,如果 x 方向的幅值遠遠大於 y 方向的值,這個距離公式就會過度放大 x 維度的作用。所以,在計算距離之前,我們可能還需要對資料進行 z-transform
: 該維度上的均值
: 該維度上的標準差
可以看到,上述處理開始體現資料的統計特性了。這種方法在假設資料各個維度不相關的情況下利用資料分佈的特性計算出不同的距離。如果維度相互之間資料相關(例如:身高較高的資訊很有可能會帶來體重較重的資訊,因為兩者是有關聯的),這時候就要用到馬氏距離(Mahalanobis distance)了。
2. 馬氏距離
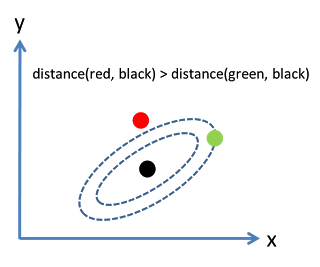
考慮下面這張圖,橢圓表示等高線,從歐幾里得的距離來算,綠黑距離大於紅黑距離,但是從馬氏距離,結果恰好相反:
馬氏距離實際上是利用 Cholesky transformation 來消除不同維度之間的相關性和尺度不同的性質。假設樣本點(列向量)之間的協方差對稱矩陣是 , 通過 Cholesky Decomposition(實際上是對稱矩陣 LU 分解的一種特殊形式,可參考之前的部落格)可以轉化為下三角矩陣和上三角矩陣的乘積:
。消除不同維度之間的相關性和尺度不同,只需要對樣本點 x 做如下處理:
。處理之後的歐幾里得距離就是原樣本的馬氏距離:為了書寫方便,這裡求馬氏距離的平方):
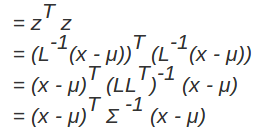
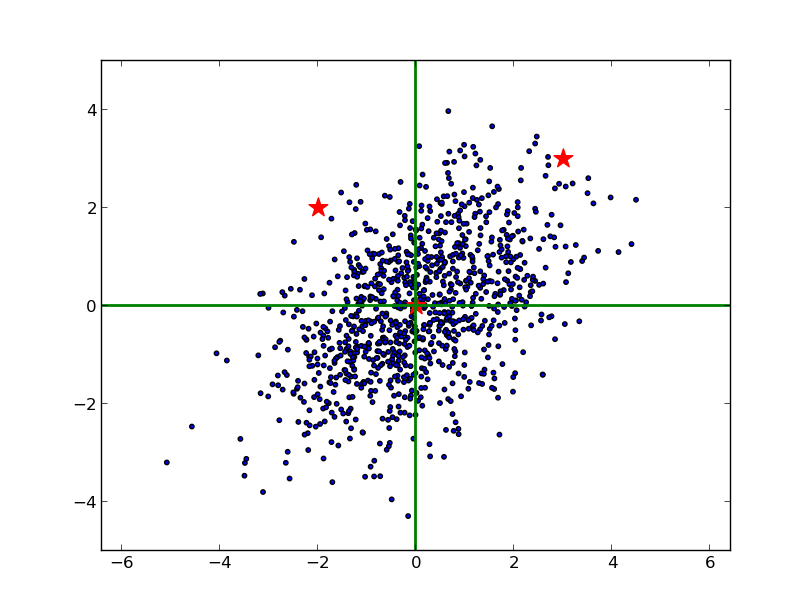
下圖藍色表示原樣本點的分佈,兩顆紅星座標分別是(3, 3),(2, -2):
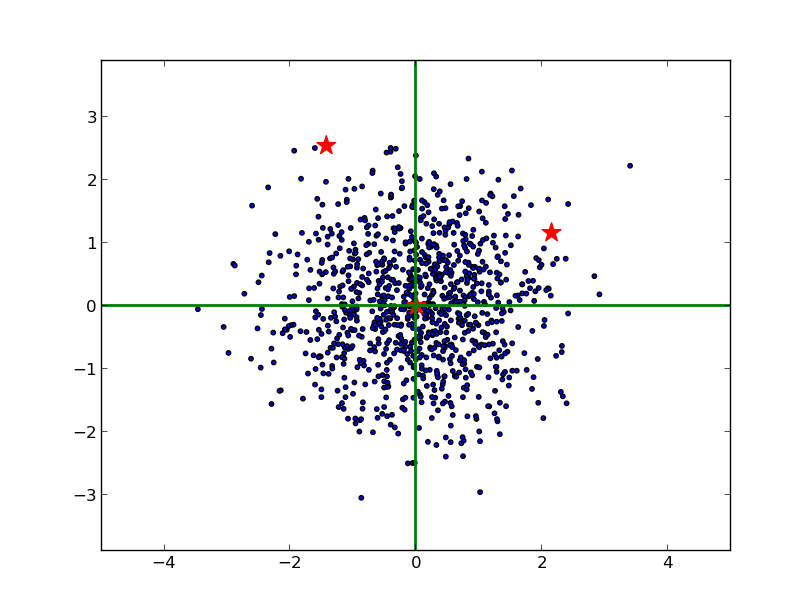
由於 x, y 方向的尺度不同,不能單純用歐幾里得的方法測量它們到原點的距離。並且,由於 x 和 y 是相關的(大致可以看出斜向右上),也不能簡單地在 x 和 y 方向上分別減去均值,除以標準差。最恰當的方法是對原始資料進行 Cholesky 變換,即求馬氏距離(可以看到,右邊的紅星離原點較近):
將上面兩個圖的繪製程式碼和求馬氏距離的程式碼貼在這裡,以備以後查閱:


1 # -*- coding=utf-8 -*- 2 3 # code related at: http://www.cnblogs.com/daniel-D/ 4 5 import numpy as np 6 import pylab as pl 7 import scipy.spatial.distance as dist 8 9 10 def plotSamples(x, y, z=None): 11 12 stars = np.matrix([[3., -2., 0.], [3., 2., 0.]]) 13 if z is not None: 14 x, y = z * np.matrix([x, y]) 15 stars = z * stars 16 17 pl.scatter(x, y, s=10) # 畫 gaussian 隨機點 18 pl.scatter(np.array(stars[0]), np.array(stars[1]), s=200, marker='*', color='r') # 畫三個指定點 19 pl.axhline(linewidth=2, color='g') # 畫 x 軸 20 pl.axvline(linewidth=2, color='g') # 畫 y 軸 21 22 pl.axis('equal') 23 pl.axis([-5, 5, -5, 5]) 24 pl.show() 25 26 27 # 產生高斯分佈的隨機點 28 mean = [0, 0] # 平均值 29 cov = [[2, 1], [1, 2]] # 協方差 30 x, y = np.random.multivariate_normal(mean, cov, 1000).T 31 plotSamples(x, y) 32 33 covMat = np.matrix(np.cov(x, y)) # 求 x 與 y 的協方差矩陣 34 Z = np.linalg.cholesky(covMat).I # 仿射矩陣 35 plotSamples(x, y, Z) 36 37 # 求馬氏距離 38 print '\n到原點的馬氏距離分別是:' 39 print dist.mahalanobis([0,0], [3,3], covMat.I), dist.mahalanobis([0,0], [-2,2], covMat.I) 40 41 # 求變換後的歐幾里得距離 42 dots = (Z * np.matrix([[3, -2, 0], [3, 2, 0]])).T 43 print '\n變換後到原點的歐幾里得距離分別是:' 44 print dist.minkowski([0, 0], np.array(dots[0]), 2), dist.minkowski([0, 0], np.array(dots[1]), 2)View Code
馬氏距離的變換和 PCA 分解的白化處理頗有異曲同工之妙,不同之處在於:就二維來看,PCA 是將資料主成分旋轉到 x 軸(正交矩陣的酉變換),再在尺度上縮放(對角矩陣),實現尺度相同。而馬氏距離的 L逆矩陣是一個下三角,先在 x 和 y 方向進行縮放,再在 y 方向進行錯切(想象矩形變平行四邊形),總體來說是一個沒有旋轉的仿射變換。
3. 向量內積
向量內積是線性代數裡最為常見的計算,實際上它還是一種有效並且直觀的相似性測量手段。向量內積的定義如下:
直觀的解釋是:如果 x 高的地方 y 也比較高, x 低的地方 y 也比較低,那麼整體的內積是偏大的,也就是說 x 和 y 是相似的。舉個例子,在一段長的序列訊號 A 中尋找哪一段與短序列訊號 a 最匹配,只需要將 a 從 A 訊號開頭逐個向後平移,每次平移做一次內積,內積最大的相似度最大。訊號處理中 DFT 和 DCT 也是基於這種內積運算計算出不同頻域內的訊號組分(DFT 和 DCT 是正交標準基,也可以看做投影)。向量和訊號都是離散值,如果是連續的函式值,比如求區間[-1, 1] 兩個函式之間的相似度,同樣也可以得到(係數)組分,這種方法可以應用於多項式逼近連續函式,也可以用到連續函式逼近離散樣本點(最小二乘問題,)中,扯得有點遠了- -!。
向量內積的結果是沒有界限的,一種解決辦法是除以長度之後再求內積,這就是應用十分廣泛的餘弦相似度(Cosine similarity):
餘弦相似度與向量的幅值無關,只與向量的方向相關,在文件相似度(TF-IDF)和圖片相似性(histogram)計算上都有它的身影。需要注意一點的是,餘弦相似度受到向量的平移影響,上式如果將 x 平移到 x+1, 餘弦值就會改變。怎樣才能實現平移不變性?這就是下面要說的皮爾遜相關係數(Pearson correlation),有時候也直接叫相關係數:
皮爾遜相關係數具有平移不變性和尺度不變性,計算出了兩個向量(維度)的相關性。不過,一般我們在談論相關係數的時候,將 x 與 y 對應位置的兩個數值看作一個樣本點,皮爾遜係數用來表示這些樣本點分佈的相關性。
由於皮爾遜係數具有的良好性質,在各個領域都應用廣泛,例如,在推薦系統根據為某一使用者查詢喜好相似的使用者,進而提供推薦,優點是可以不受每個使用者評分標準不同和觀看影片數量不一樣的影響。
4. 分類資料點間的距離
漢明距離(Hamming distance)是指,兩個等長字串s1與s2之間的漢明距離定義為將其中一個變為另外一個所需要作的最小替換次數。舉個維基百科上的例子:

還可以用簡單的匹配係數來表示兩點之間的相似度——匹配字元數/總字元數。
在一些情況下,某些特定的值相等並不能代表什麼。舉個例子,用 1 表示使用者看過該電影,用 0 表示使用者沒有看過,那麼使用者看電影的的資訊就可用 0,1 表示成一個序列。考慮到電影基數非常龐大,使用者看過的電影只佔其中非常小的一部分,如果兩個使用者都沒有看過某一部電影(兩個都是 0),並不能說明兩者相似。反而言之,如果兩個使用者都看過某一部電影(序列中都是 1),則說明使用者有很大的相似度。在這個例子中,序列中等於 1 所佔的權重應該遠遠大於 0 的權重,這就引出下面要說的傑卡德相似係數(Jaccard similarity)。
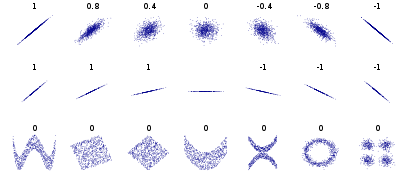
在上面的例子中,用 M11 表示兩個使用者都看過的電影數目,M10 表示使用者 A 看過,使用者 B 沒看過的電影數目,M01 表示使用者 A 沒看過,使用者 B 看過的電影數目,M00 表示兩個使用者都沒有看過的電影數目。Jaccard 相似性係數可以表示為:
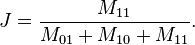
Jaccard similarity 還可以用集合的公式來表達,這裡就不多說了。
如果分類數值點是用樹形結構來表示的,它們的相似性可以用相同路徑的長度來表示,比如,“/product/spot/ballgame/basketball” 離“product/spot/ballgame/soccer/shoes” 的距離小於到 "/product/luxury/handbags" 的距離,以為前者相同父節點路徑更長。
5. 序列之間的距離
上一小節我們知道,漢明距離可以度量兩個長度相同的字串之間的相似度,如果要比較兩個不同長度的字串,不僅要進行替換,而且要進行插入與刪除的運算,在這種場合下,通常使用更加複雜的編輯距離(Edit distance, Levenshtein distance)等演算法。編輯距離是指兩個字串之間,由一個轉成另一個所需的最少編輯操作次數。許可的編輯操作包括將一個字元替換成另一個字元,插入一個字元,刪除一個字元。編輯距離求的是最少編輯次數,這是一個動態規劃的問題,有興趣的同學可以自己研究研究。
時間序列是序列之間距離的另外一個例子。DTW 距離(Dynamic Time Warp)是序列訊號在時間或者速度上不匹配的時候一種衡量相似度的方法。神馬意思?舉個例子,兩份原本一樣聲音樣本A、B都說了“你好”,A在時間上發生了扭曲,“你”這個音延長了幾秒。最後A:“你~~~好”,B:“你好”。DTW正是這樣一種可以用來匹配A、B之間的最短距離的演算法。
DTW 距離在保持訊號先後順序的限制下對時間訊號進行“膨脹”或者“收縮”,找到最優的匹配,與編輯距離相似,這其實也是一個動態規劃的問題:



1 #!/usr/bin/python2 2 # -*- coding:UTF-8 -*- 3 # code related at: http://blog.mckelv.in/articles/1453.html 4 5 import sys 6 7 distance = lambda a,b : 0 if a==b else 1 8 9 def dtw(sa,sb): 10 ''' 11 >>>dtw(u"幹啦今今今今今天天氣氣氣氣氣好好好好啊啊啊", u"今天天氣好好啊") 12 2 13 ''' 14 MAX_COST = 1<<32 15 #初始化一個len(sb) 行(i),len(sa)列(j)的二維矩陣 16 len_sa = len(sa) 17 len_sb = len(sb) 18 # BUG:這樣是錯誤的(淺拷貝): dtw_array = [[MAX_COST]*len(sa)]*len(sb) 19 dtw_array = [[MAX_COST for i in range(len_sa)] for j in range(len_sb)] 20 dtw_array[0][0] = distance(sa[0],sb[0]) 21 for i in xrange(0, len_sb): 22 for j in xrange(0, len_sa): 23 if i+j==0: 24 continue 25 nb = [] 26 if i > 0: nb.append(dtw_array[i-1][j]) 27 if j > 0: nb.append(dtw_array[i][j-1]) 28 if i > 0 and j > 0: nb.append(dtw_array[i-1][j-1]) 29 min_route = min(nb) 30 cost = distance(sa[j],sb[i]) 31 dtw_array[i][j] = cost + min_route 32 return dtw_array[len_sb-1][len_sa-1] 33 34 35 def main(argv): 36 s1 = u'幹啦今今今今今天天氣氣氣氣氣好好好好啊啊啊' 37 s2 = u'今天天氣好好啊' 38 d = dtw(s1, s2) 39 print d 40 return 0 41 42 if __name__ == '__main__': 43 sys.exit(main(sys.argv))View Code
6. 概率分佈之間的距離
前面我們談論的都是兩個數值點之間的距離,實際上兩個概率分佈之間的距離是可以測量的。在統計學裡面經常需要測量兩組樣本分佈之間的距離,進而判斷出它們是否出自同一個 population,常見的方法有卡方檢驗(Chi-Square)和 KL 散度( KL-Divergence),下面說一說 KL 散度吧。
先從資訊熵說起,假設一篇文章的標題叫做“黑洞到底吃什麼”,包含詞語分別是 {黑洞, 到底, 吃什麼}, 我們現在要根據一個詞語推測這篇文章的類別。哪個詞語給予我們的資訊最多?很容易就知道是“黑洞”,因為“黑洞”這個詞語在所有的文件中出現的概率太低啦,一旦出現,就表明這篇文章很可能是在講科普知識。而其他兩個詞語“到底”和“吃什麼”出現的概率很高,給予我們的資訊反而越少。如何用一個函式 h(x) 表示詞語給予的資訊量呢?第一,肯定是與 p(x) 相關,並且是負相關。第二,假設 x 和 y 是獨立的(黑洞和宇宙不相互獨立,談到黑洞必然會說宇宙),即 p(x,y) = p(x)p(y), 那麼獲得的資訊也是疊加的,即 h(x, y) = h(x) + h(y)。滿足這兩個條件的函式肯定是負對數形式:
對假設一個傳送者要將隨機變數 X 產生的一長串隨機值傳送給接收者, 接受者獲得的平均資訊量就是求它的數學期望:
這就是熵的概念。另外一個重要特點是,熵的大小與字元平均最短編碼長度是一樣的(shannon)。設有一個未知的分佈 p(x), 而 q(x) 是我們所獲得的一個對 p(x) 的近似,按照 q(x) 對該隨機變數的各個值進行編碼,平均長度比按照真實分佈的 p(x) 進行編碼要額外長一些,多出來的長度這就是 KL 散度(之所以不說距離,是因為不滿足對稱性和三角形法則),即:
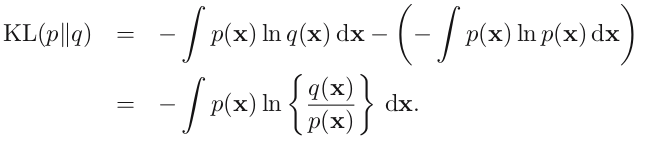
KL 散度又叫相對熵(relative entropy)。瞭解機器學習的童鞋應該都知道,在 Softmax 迴歸(或者 Logistic 迴歸),最後的輸出節點上的值表示這個樣本分到該類的概率,這就是一個概率分佈。對於一個帶有標籤的樣本,我們期望的概率分佈是:分到標籤類的概率是 1, 其他類概率是 0。但是理想很豐滿,現實很骨感,我們不可能得到完美的概率輸出,能做的就是儘量減小總樣本的 KL 散度之和(目標函式)。這就是 Softmax 迴歸或者 Logistic 迴歸中 Cost function 的優化過程啦。(PS:因為概率和為 1,一般的 logistic 二分類的圖只畫了一個輸出節點,隱藏了另外一個)
