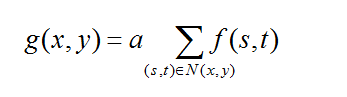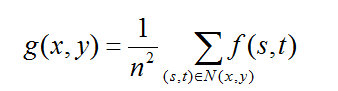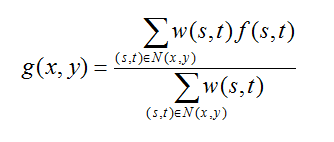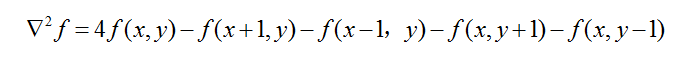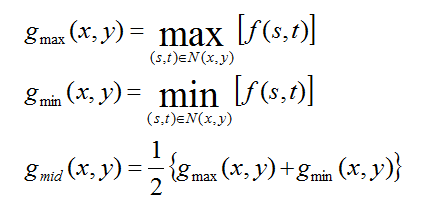一、學習心得： 在我學習基本濾波演算法原理的時候，因為剛接觸不是很理解演算法具體是怎樣實現的，不過在學習了影象形態學之後，發現濾波演算法其實很簡單。所以在此建議初學者在學習濾波演算法之前，可以先學習一下影象形態學，會達到事半功倍的效果。

二、對於濾波功能的理解： 濾波演算法，可以理解成一種過濾演算法，就像我們篩選產品時，把次品去除掉，只留下合格的產品。而在影象處理中的濾波演算法中，處理的物件是影象，除了去除掉影象中不想要的畫素點的值（如去除噪聲），還可以加強影象中我們需要研究一些內容（如邊緣提取）。

三、濾波演算法： 這裡所講的演算法都是針對影象空間的濾波演算法，其中模板，可以理解為影象形態學中的結構元素，是用來選取影象中的那些畫素點被用來操作的。空間濾波根據其功能劃分為平滑濾波和銳化濾波。平滑濾波：

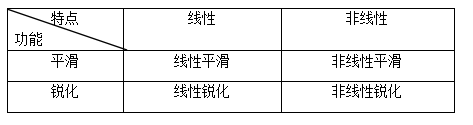
空間增強濾波技術分類：

1、線性平滑濾波

（1）方框濾波：用一個畫素的領域畫素值之和作為濾波結果，鄰域即模板所覆蓋的影象區域，此時模板的所有係數都為1.

（2）鄰域平均：是特殊大方框濾波，用一個畫素的領域平均畫素值作為濾波結果，即a為第一種情。

其中N(x,y)為模板歲覆蓋的影象的區域，n為模板的尺寸。

（3）加權平均：此時的模板係數不是1，而是具體的係數。一般認為距離模板中心的畫素應對濾波結果有較大的貢獻，所以可將接近模板中心的係數取得比模板周邊的係數。

（4）高斯平均：是一種特殊的加權平均，只不過模板中的係數由高斯分佈來確定的。

2、線性銳化濾波

（1）拉普拉斯運算元 拉普拉斯運算元是一種各向同性的二階微分運算元，利用微分系數來確定模板係數，然後再與影象進行卷積運算，從而實現銳化濾波。

根據拉普拉斯定義： 兩個分別沿X和Y方向的二階偏導均可藉助差分計算： 合併為：

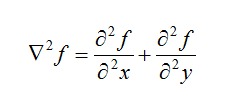
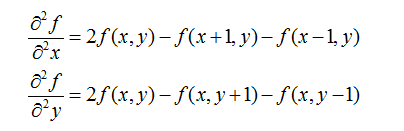
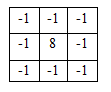
當模板為4-鄰域時 當模板為8-鄰域時

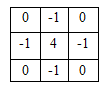
  以上兩種模板的係數之和為0，這是為了使經過模板運算的影象的均值不變。拉普拉斯運算元增強了影象中的灰度不連續區域，而減弱了影象中灰度值緩慢變化區域對比度，將這樣的結果疊加到原始影象中，就可以得到瑞華後的額影象。
 

• 1

（2）高頻提升濾波 影象的銳化效果可以通過疊加影象的微分結果得到，也可以通過減除影象積分結果得到。 設原始影象為f(x,y),平滑後的影象為g(x,y)：

非銳化掩模：h(x,y) = f(x,y)-g(x,y)

銳化影象：{ f(x,y)- g(x,y) } + f(x,y）

高頻提升濾波：把院士圖形乘以一個放大係數A，再減去平滑影象

可轉化為： 當A=1時，為非銳化掩模； 當A=2時，為非銳化掩模化。

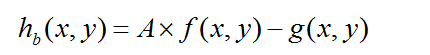
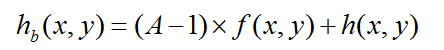
3、非線性平滑濾波

（1）中值濾波：對模板下對應的畫素值進行升序排序，選取中間值作為結果。 （2）與中值濾波類似的，還有最大值、最小值、中點濾波

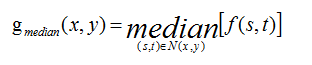
以上四種濾波也稱之為百分比濾波，百分比濾波基於模板的排序來工作，又叫作序統計濾波。