唯一路徑
Unique Paths
A robot is located at the top-left corner of a m x n grid (marked ‘Start’ in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).
How many possible unique paths are there?
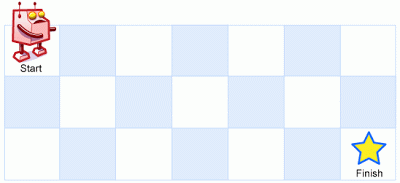
Above is a 3 x 7 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
題目大意
在一個m*n的表格中,從左上角的起點處走到右下角的終點處共有多少條不同的路徑。
在本題中,上圖中的表格是3*7的一個表格,有多少種不同的路徑。
思路
動態規劃思想
這是一個典型的入門級動態規劃問題,很容易想到動態規劃的思路。
二維陣列動態規劃
把問題中的m*n的表格翻譯成m*n的二維陣列,原理是除了第一行或者第一列的格子外,到其他格子路徑的走法是:每一個格子的可到達路徑數=左邊一個格子的可到達路徑數+上邊一個格子的可到達路徑數
一維陣列動態規劃
用一維陣列代替二維陣列,動態更新。時間複雜度為O(N^2),空間複雜度為O(N)。
組合數學思想
組合數學的思想是,從左上角的起點處走到右下角的終點處,只能向右走或者只能向下走,從行上看走過了m - 1行,從列上看走過了n - 1列,即可以理解為排列組合的問題,所以一共需要的步數中挑出m - 1個向下走,剩下的n - 1個就是向右走,其實就是從(m-1+n-1)裡挑選(n-1)或者(m-1)個,即:C(n,r),其中n = (m-1+n-1),r = (n-1)
n! / ( r! * (n - r)! )。
程式碼
動態規劃(二維陣列)
int uniquePaths(int m, int n) {
// 用vector定義int型別的二維陣列,並全部初始化為1
vector<vector<int > > dp(m, vector<int >(n, 1));
for(int i=1; i<m; i++)
{
for(int j=1; j<n; j++)
{
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}//for
}//for
return dp[m-1][n-1];
}
動態規劃(一維陣列)
int uniquePaths(int m, int n) {
// 用vector定義int型別的一維陣列,並全部初始化為1
vector<int > dp(n, 1);
for(int i=1; i<m; i++)
{
for(int j=1; j<n; j++)
{
// 用一維陣列模擬二維陣列,動態更新當前行
dp[j] += dp[j-1];
}//for
}//for
return dp[n-1];
}
組合數學(排列組合)
int uniquePaths(int m, int n)
{
long x = m+n-2;// 不用 long 會溢位,階乘求出來太大了
long y = min(m,n)-1;
long up = 1,down =1;// 最後求組合數的分子 / 分母
// if(m==1||n==1) return 1;
for(int i = 0;i<y ;i++)
{
up *= x--;
}
for(int i = y; i>0; i--)
{
down *= i;
}
return int(up/down);
}
以上。
版權宣告:本文為博主原創文章,轉載請註明出處。
個人部落格地址:https://yangyuanlin.club
歡迎來踩~~~~
