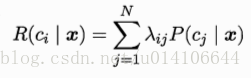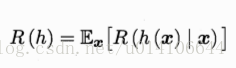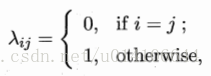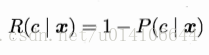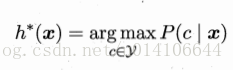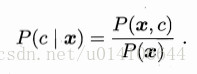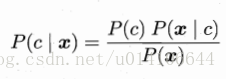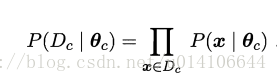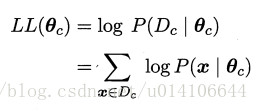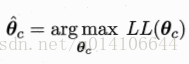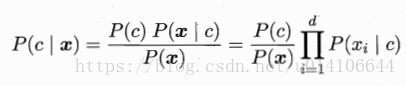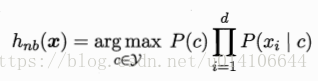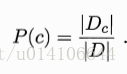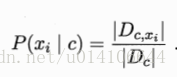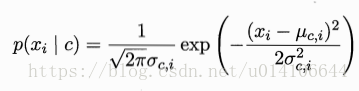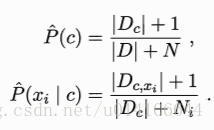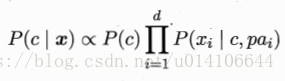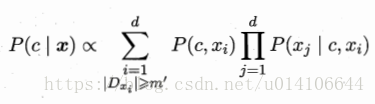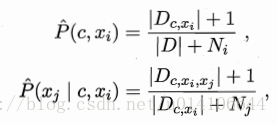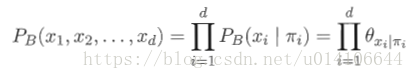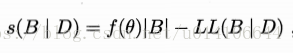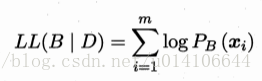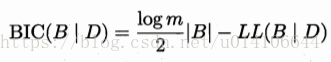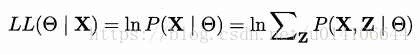機器學習演算法--貝葉斯分類器
1.貝葉斯理論
在已知相關概率下,基於概率和誤判損失來選擇最優的類別標記。
假設類別標記總數為N,即Y{c1,c2..cn}.rij表示將一個真實樣本為cj誤判為ci的損失,p(ci|x)表示樣本x分類為ci的概率,則有樣本x的條件風險:
尋找一個判定準則h,使得X---->Y,總體風險最小
貝葉斯判定準則:對於每個樣本x,若R(h(x)|x)最小,則總體風險R(h)也將最小。
h*為最優貝葉斯分類器,R(h*)為貝葉斯風險,對於每個樣本,選擇那個條件風險R(c|x)最小的類別標記
若最小化分類錯誤率,損失函式:
則樣本x的條件風險:
最小化分類錯誤率的最優貝葉斯分類器:
欲求P(c|x)的最大值,有
P(c)為樣本中各個類別的概率 P(x|c)是樣本在分類c下的特徵屬性分佈概率 P(x)是樣本x分佈概率,與類別標記無關。
P(c)表達了樣本中各個類別的比重,可以利用樣本中的類別數量頻率來進行估計;P(x|c)是樣本在已知分類為c的條件下,各個特徵屬性的聯合分佈,x為樣本特徵向量,一般多維,聯合概率難以求解和估計。
2.極大似然估計
估計類條件概率一般採用極大似然估計,即先假定具有某種確定的概率分佈形式,再基於訓練樣本對概率分佈引數進行估計。結果的準確依賴於假設的分佈是否接近於資料真實的分佈。
Dc表示訓練集中第c類樣本組成的集合,假定這些樣本獨立同分布,則引數oc對於Dc的似然估計為:
即求得引數oc,使得樣本所有可能出現的可能性最大
為了避免連乘造成下溢,取對數似然:
即引數似然估計的任務:
3.樸素貝葉斯分類器NBC
P(x|c)表示已知類別c下的屬性聯合分佈,x=(x1,x2...xd)為d喂向量,一般難於求解,NBC假設x的所有特徵屬性相互獨立,獨立的對於結果發生影響,基於條件屬性獨立性假設:
NBC分類屬性表示式,即
類先驗概率P(c) Dc表示訓練集D中c類樣本數
對於離散屬性: Dcxi表示第c類中第一個屬性值為xi的樣本數
對於連續屬性 假定 其中第c類樣本中第i個屬性取值的均值和方差(多維高斯分佈)
說明:
中心極限定理:樣本的平均值約等於總體的平均值。不管總體是什麼分佈,任意一個總體的樣本平均值都會圍繞在總體的整體平均值周圍,並且呈正態分佈。
拉普拉斯平滑:為避免訓練集中其他屬性被未出現的屬性而抹去,需要進行平滑,避免因訓練集樣本不充分而出現概率為0的情況
N表示訓練集D中可能的類別數,Ni表示第i個屬性可能的取值數
4.半樸素貝葉斯分類器SNBC
獨依賴估計(ODE)假設每個屬性依賴於類別之外最多僅依賴於一個其他屬性
pai為屬性xi的依賴屬性,稱為xi的父屬性。如何為每個屬性確定父屬性:
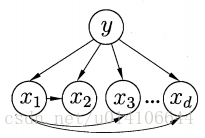
1.SPODE
假設所有屬性依賴於同一個超父屬性,通過交叉驗證來確定最優超父屬性
2.TAN
利用最大帶權生成樹演算法
(1)計算任意兩個屬性之前的條件互資訊
(2)以屬性為節點構建完全圖,權重為條件互資訊
(3)構建最大帶權生成樹
(4)加入類別屬性y,增加y到各個屬性的有向邊
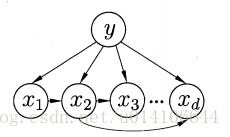
3.AODE
採用整合學習,將每個屬性作為父屬性來構建SPOED,然後選取那些足夠訓練資料的SPODE來整合學習
Dxi是第i個屬性上取值為xi的樣本集合,m`為閾值
Dcxi表示類別為c且第i個屬性為xi的樣本集合 N表示D中可能類別數 Ni表示第i個屬性可能取值數
Dcxixj 表示類別為c且第i屬性為xi,第j個屬性為xj的樣本集合
5.貝葉斯網
5.1結構
貝葉斯網由網路結構G和引數O組成 B=<G,O> G是一個有向無環圖 O描述這種依賴關係。
給定某個節點,貝葉斯網假定屬性與他的非後裔屬性獨立
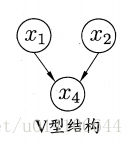
分析變數間的條件獨立性,有向分解,將有向圖變為無向圖:找出圖中所有V型結構,在兩個父節點之間新增一條無向邊,將圖中所有有向邊變為無向邊,變為道德圖
在道德圖中,變數x,y,能被屬性集合Z={zi}分開,則說明在Z的條件下,x和y獨立
5.2網路結構學習
評分函式:
其中|B|為貝葉斯網路的引數 f(O)為每個引數的編碼長度 LL(B|D)為貝葉斯網的對數似然
AIC f(O)=1
BIC f(O)=logm/2
從所有可能空間搜尋貝葉斯網是NP難問題,可以近似求解 1貪心法 逐漸增加邊的數量 2施加約束來不斷減少邊的數量。
5.3推斷
吉布斯取樣演算法:
Q={Q1,Q2..Qn}待查詢的變數
E={E1,E2...Ek}證據變數 取值e={e1,e2...ek}
計算P(Q=q|E=e) q={q1,q2..qn}待查詢變數的一組取值
吉布斯取樣演算法:
6.EM演算法
未觀測變數為隱變數 X已觀測變數 Z隱變數 O引數
對引數O進行最大似然估計
計算Z期望來最大化已觀測資料的邊際似然
E步:以當前引數的估計值來計算對數似然的期望值
M步:尋找使E中對數似然最大的引數值