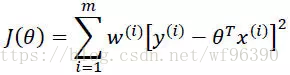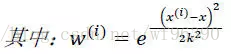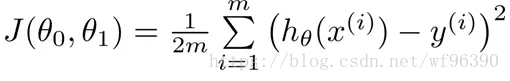什麼是機器學習

作為機器學習領域的先驅，Arthur Samuel在 IBM Journal of Research and Development期刊上發表了一篇名為《Some Studies in Machine Learning Using the Game of Checkers》的論文中，將機器學習非正式定義為：”在不直接針對問題進行程式設計的情況下，賦予計算機學習能力的一個研究領域。”

Tom Mitchell在他的《Machine Learning（中文版：電腦科學叢書:機器學習 ）》一書的序言開場白中給出了一個定義：

“機器學習這門學科所關注的問題是：計算機程式如何隨著經驗積累自動提高效能。”

“對於某類任務T和效能度量P，如果一個計算機程式在T上以P衡量的效能隨著經驗E而自我完善，那麼我們稱這個計算機程式在從經驗E學習。”

他沒有告訴機器應該怎麼下棋，機器可以自己不斷學習如何下棋，因此把這一過程帶入到定義中，我們知道：

E：機器不斷下棋的經歷 T：下棋 P：下棋的勝率

機器學習分類

1.監督學習（Supervised Learning）

有標準答案（有標籤）

• regression 迴歸問題（連續） 例：房價變化

• classification 分類問題（離散） 例：字元識別

2.非監督學習（Unsupervised Learning）

沒有標準答案（無標籤）

• K-means聚類

• PCA

3.強化學習/反饋學習（Reinforcement Learning）

你在訓練一隻狗，每次狗做了一些你滿意的事情，你就說一聲“Good boy” 然後獎勵它。每次狗做了something bad 你就說 "bad dog "，漸漸的，狗學會了做正確的事情來獲取獎勵。

強化學習與其他機器學習不同之處為：

• 沒有教師訊號，也沒有label。只有reward，其實reward就相當於label。
• 反饋有延時，不是能立即返回。
• 相當於輸入資料是序列資料。
• agent執行的動作會影響之後的資料。

常用的字母表示

m => training examples 訓練資料數目

x => input variables/features 輸入變數

y => output/target variable

(x, y) => training example

theta => parameters

               training set

                    |

           learning algorithm

                    |

input ->     h(hypothesis)     -> output

一元線性迴歸

迴歸分析（Regression Analysis)是確定兩種或兩種以上變數間相互依賴的定量關係的一種統計分析方法。在迴歸分析中，只包括一個自變數和一個因變數，且二者的關係可用一條直線近似表示，這種迴歸分析稱為一元線性迴歸分析。

舉個例子：可以根據房子的平米數來估算房價

一元線性方程公式： ，可以用作擬合函式

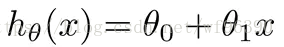
如何求解擬合函式可以使用最小二乘法，所謂最小二乘，其實也可以叫做最小平方和。就是讓目標物件和擬合物件的誤差最小。即通過最小化誤差的平方和，使得擬合物件無限接近目標物件，這就是最小二乘的核心思想。所以把擬合值和實際值的差求平方和，可以得到損失函式，最小化損失函式可以得到

求解方法 方法一：梯度下降 步長選擇：步長過小—收斂太慢 步長過大—無法收斂

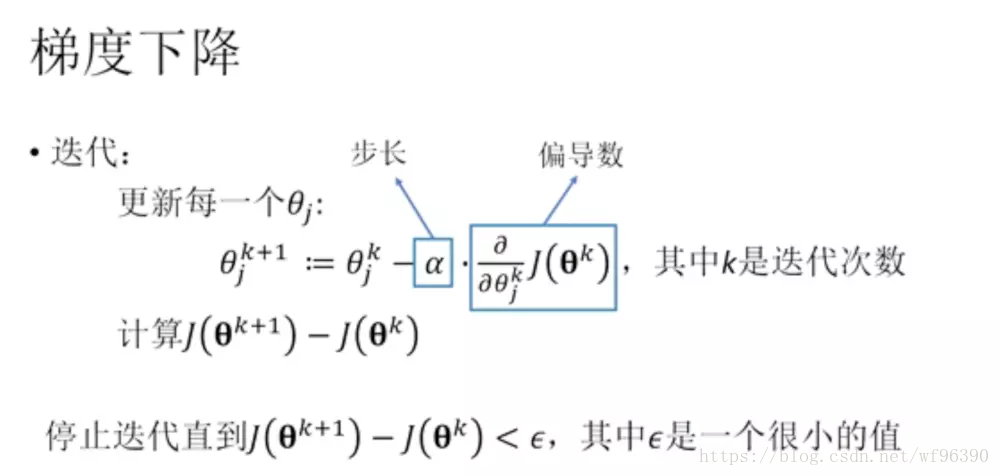
批量梯度下降（Batch gradient descent ） 全域性最優，資料量太大無法計算

隨機梯度下降（Stochastic gradient descent） 適合於低精度的任務

方法二：正規方程組

兩種方法比較： 欠擬合和過擬合 首先我們來看一個線性迴歸的問題，在下面的例子中，我們選取不同維度的特徵來對我們的資料進行擬合。

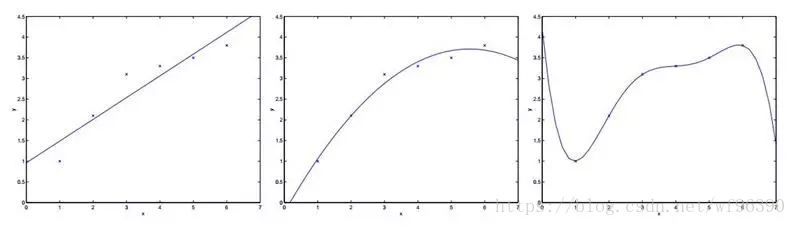
對於上面三個影象做如下解釋：

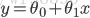
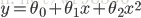
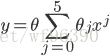
選取一個特徵x， 來擬合數據，可以看出來擬合情況並不是很好，有些資料誤差還是比較大。 針對第一個，我們增加了額外的特徵 ， ，這時我們可以看出情況就好了很多。 這個時候可能有疑問，是不是特徵選取的越多越好，維度越高越好呢？所以針對這個疑問，如最右邊圖，我們用5揭多項式使得資料點都在同一條曲線上，為 。此時它對於訓練集來說做到了很好的擬合效果，但是，我們不認為它是一個好的假設，因為它不能夠做到更好的預測。

針對上面的分析，我們認為第二個是一個很好的假設，而第一個圖我們稱之為欠擬合（underfitting），而最右邊的情況我們稱之為過擬合（overfitting）

區域性加權線性迴歸

對於線性迴歸演算法，一旦擬合出適合訓練資料的引數θi’s，儲存這些引數θi’s，對於之後的預測，不需要再使用原始訓練資料集，所以是引數學習演算法。

對於區域性加權線性迴歸演算法，每次進行預測都需要全部的訓練資料（每次進行的預測得到不同的引數θi’s），沒有固定的引數θi’s，所以是非引數演算法。 對於上述公式的理解是這樣的：x為某個預測點，x^((i))為樣本點，樣本點距離預測點越近，貢獻的誤差越大（權值越大），越遠則貢獻的誤差越小（權值越小）。關於預測點的選取，在我的程式碼中取的是樣本點。其中k是頻寬引數，控制w（鐘形函式）的寬窄程度，類似於高斯函式的標準差。