從自然數1,2,...,n中任取r個數的所有組合
阿新 • • 發佈:2018-12-17
【問題】利用遞迴方法找出從自然數1,2,…,n中任取r個數的所有組合
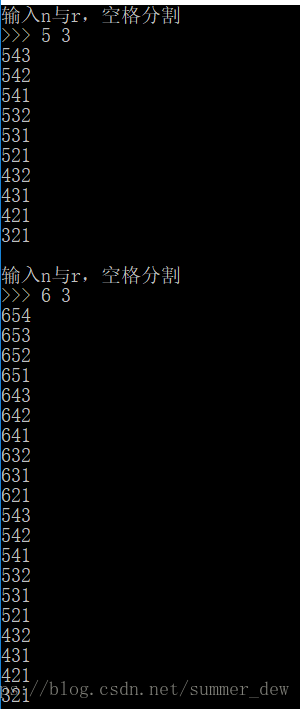
【例如】n=5,r=3,所有組合為:
方法一
【思路】
- 抽象問題:1,…,n中選r --> f(n,r)
- 從邊界n考慮,n要麼取,要麼不取 --> f(n,r) = f(n-1, r) + f(n-1, r-1)
- 退出條件:r==0時,就已經選完了
- 異常條件:n<r的時候
int a[50];
void f(int n,int r,int m) {
int i;
if (n<r) return ;
if (r==0) {
for (i=0; i<m; i++) printf("%d" 方法二
【程式碼】
// 從1-n的數字中選r個數字
// 目前選的一個放入a[m]位置中
void C(int n, int r, int a[], int m) {
int i;
if (r==0) { //選完了
//輸出
for (i=0; i<m; i++) printf("%d", a[i]);
printf("\n");
} else {
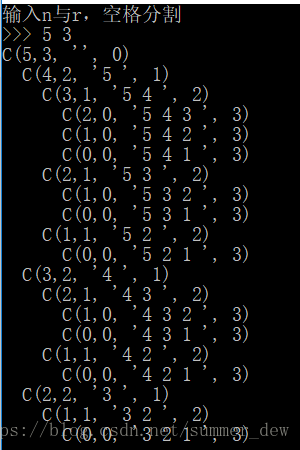
// 在[r,n]的範圍內選一個數字放入a[m] 【理解】用樹狀的形式輸出遞迴樹(先序)
樹狀的方式類似於這種https://blog.csdn.net/summer_dew/article/details/82937941
完整程式碼
方法一:
#include<stdio.h>
int a[50];
void f(int n,int r,int m) {
int i;
if (n<r) return ;
if (r==0) {
for (i=0; i<m; i++ 方法二:
#include<stdio.h>
// 從1-n的數字中選r個數字
// 目前選的一個放入a[m]位置中
void C(int n, int r, int a[], int m) {
int i;
// 以樹狀輸出遞迴樹
/*
for (i=0; i<m; i++) {
printf(" ");
}
printf( "C(%d,%d, '" , n,r);
for (i=0; i<m; i++) {
printf("%d ", a[i]);
}
printf("', %d)",m );
printf("\n");
*/
if (r==0) { // 選完了
// 輸出
for (i=0; i<m; i++) printf("%d", a[i]);
printf("\n");
} else {
// 在[r,n]的範圍內選一個數字放入a[m]
for (i=n; i>=r; i--) {
a[m] = i;
C(i-1, r-1, a, m+1);
}
}
}
int main() {
int n,r;
int a[50];
while (1) {
printf("輸入n與r,空格分割\n>>> ");
scanf("%d%d", &n, &r);
C(n, r, a, 0);
printf("\n");
}
return 0;
}