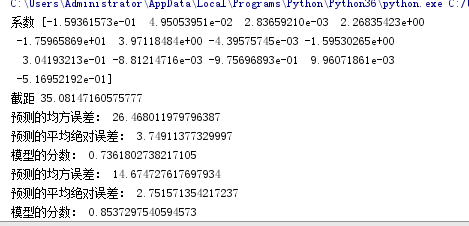
#一、boston房價預測
#匯入載入包
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# 讀取波士頓房價資料集
data = load_boston()

# 劃分資料集
x_train, x_test, y_train, y_test = train_test_split(data.data,data.target,test_size=0.2)

 
# 建立多元線性迴歸模型
mlr = LinearRegression()
mlr.fit(x_train,y_train)
print('係數',mlr.coef_,"\n截距",mlr.intercept_)

# 檢測模型好壞
from sklearn.metrics import regression
y_predict = mlr.predict(x_test)
# 計算模型的預測指標
print("預測的均方誤差：", regression.mean_squared_error(y_test,y_predict))
print("預測的平均絕對誤差：", regression.mean_absolute_error(y_test,y_predict))
 
# 列印模型的分數
print("模型的分數：",mlr.score(x_test, y_test))

# 多元多項式迴歸模型
# 多項式化
poly2 = PolynomialFeatures(degree=2)
x_poly_train = poly2.fit_transform(x_train)
x_poly_test = poly2.transform(x_test)

# 建立模型
mlrp = LinearRegression()
mlrp.fit(x_poly_train, y_train)

# 預測
y_predict2 = mlrp.predict(x_poly_test)
 
# 檢測模型好壞
# 計算模型的預測指標
print("預測的均方誤差：", regression.mean_squared_error(y_test,y_predict2))
print("預測的平均絕對誤差：", regression.mean_absolute_error(y_test,y_predict2))
# 列印模型的分數
print("模型的分數：",mlrp.score(x_poly_test, y_test))
#線性模型與非線性模型的效能比較：線性模型的圖形明顯比非線性模型的影象更加貼切形象，平滑的曲線更精確地將樣本點的分佈規律展現出來，極大地減少了誤差，效能更有優勢。