深度學習讀書筆記 第二章:線性代數
2.1 標量、向量、矩陣和張量
標量:scalar,是一個單獨的數
向量:vector,是一列有序的數.方括號包圍的縱列,每個元素有一個索引。
矩陣:matrix,二維陣列,每個元素由兩個索引組成。Aij處於i行j列。
張量:tensor,超過二維的陣列。
標量和矩陣的運算:
![]()
向量和矩陣的運算:將向量隱式的複製到很多位置的方式成為廣播(broadcasting)
![]()
2.2 矩陣和向量相乘
矩陣A、B、C有C=AB,
A(m*n)、B(n*p),則C(m*p)
矩陣乘積滿足分配律A*(B+C)=A*B+A*C
結合律A*(B*C)=A*B*C
但是不滿足交換律A*B≠B*A
2.3 單位矩陣和逆矩陣
單位矩陣In(identity matrix),沿主對角線元素是1,其餘位置元素都是0.
矩陣和它的逆矩陣相乘得到單位矩陣。
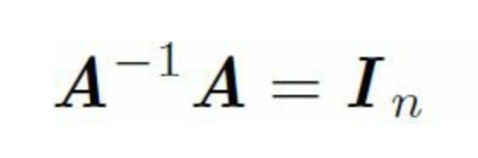
一個n維向量x和單位矩陣的乘積還是它本身x。
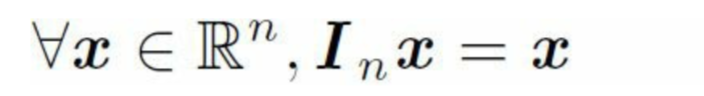
2.4 線性相關和生成子空間
A是矩陣,x是列 向量。對於Ax=b,(A:m*n, x:n維空間, b:m維空間)如果有解,向量的線性組合。如果要讓Ax=b有解,n≥m
加入A是一個3*2的矩陣 ,目標 b是3維的,而x只有2維,那麼只能得到三維空間的一個 二維平面,當且僅當b在這個二維平面上時,該方程有解。
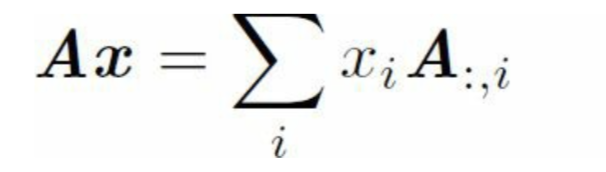
n≥m是必要條件,但不是充分條件,因為有的列向量是冗餘的,(如果兩個列向量相同,那麼他們表示的矩陣列空間是一樣的,這種冗餘稱為線性 相關)。如果一組向量中的任何一個列向量都不能表示成其他列向量的線性組合,就稱這組向量稱為線性無關。那麼,如果一個矩陣的列空間涵蓋Rm,那麼它至少有m個線性無關的列向量。
一組向量的生成子空間span,是原始向量線性組合後能抵達點的組合 。
矩陣可逆的條件:矩陣必須是一個方陣,m=n,所有列向量都是線性無關的。
2.5 範數 norm
機器學習中用範數來衡量向量的大小
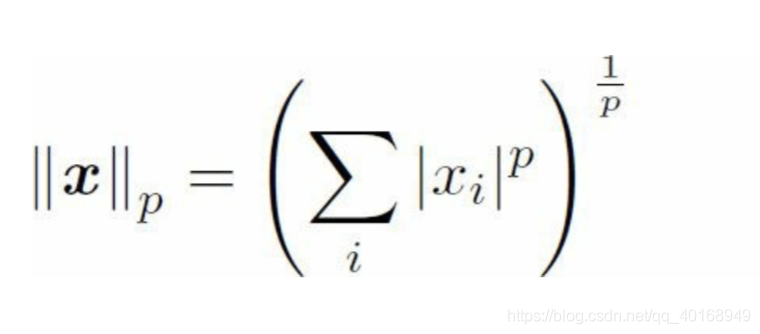
2範數又稱歐幾里得範數,表示原點到向量的距離。倒數與整個向量有關,但是在原點附近增長緩慢。在機器學習 應用中,區分 恰好是零和零附近很小的元素是很重要的,這時候1範數比較好用--斜率相同,與x增長速度相同。
有時候用非零元素的個數衡量向量的大小,因為非零元素縮放a倍並不會改變非零元素數目,因此常用1範數表示非零元素數目的替代函式。
最大範數(max norm)表示向量中具有最大幅度的元素絕對值。
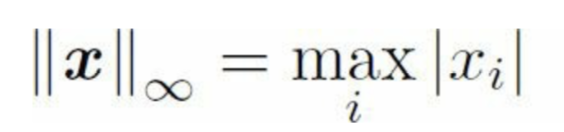
frobenius norm:針對矩陣而言 ,類比二範數。

2.6 特殊型別的矩陣和向量
對角矩陣(diagonal matrix)只有主對角線元素非零,區分於單位矩陣--對角線元素全1,其他位置全0.
並非所有對角矩陣都是方陣,非方陣的對角矩陣不存在逆矩陣。
對稱(symmetric)是矩陣轉制和自己相等的矩陣。某些不依賴引數順序的雙引數函式 生成元素時,會出現對稱矩陣,Aij=Aji.
2.7 特徵分解
將矩陣分解成一組特定的向量和特徵值。
