重溫資料結構(二)
嘿嘿嘿,哈哈哈(摩拳擦掌中)。
今天的工作做完了,讓我們開始繼續看《大話資料結構》。 ^ - ^
今天要看的是線性表。最簡單也最常用。它的英文名是List。
線性表:零個或多個數據元素的有限序列。
當線性表裡的元素為零個的時候,就稱為空表。
線性表主要分為順序儲存和鏈式儲存,先來看看簡單一點的順序儲存。
一.線性表的順序儲存
線性表的順序儲存:指的是用一段地址連續的儲存單元依次儲存線性表的資料元素。
下面來看看順序儲存的結構程式碼:
#define MAX_SIZE 100 //儲存空間初始分配量
typedef int ElemType; //ElemType 現定義為int 特別注意,length是表示當前線性表的長度,是可變的,但length不會超過data的最大長度。
下面就可以來看看基本的操作啦:
1.查詢操作
// 得到線性表L中第i個數據
void GetElem (SqList L , int i ,ElemType *e){
int currentLength = L.length;//當前線性表長度
if(currentLength == 0 注:預設線性表的長度從1開始,而預設的陣列下標從0開始,所以線性表中第i個數據對應陣列下標為i-1的資料。
2.插入操作
//線上性表中的第i個位置插入新元素e
void ListInsert(SqList *L , int i ,ElemType e){
int currentLength = L->length;
if(currentLength == MAX_SIZE || i < 1 注:把元素向後移的時候,從表尾開始,一直到陣列下標為i-1為止。插入新元素e後,記得將線性表長度+1。
2.刪除操作
//刪除線性表的第i個位置的元素
void ListDelete(SqList *L,int i,ElemType *e){
int currentLength = L->length;
if(currentLength == 0 || i > currentLength || i < 1){
//空表,越界
}else{
*e = L->data[i-1];//需要可用於儲存資料,不需要則去除
if(i < currentLength){//如果i不在表尾
for(int k = i -1; k < currentLength - 1; k++){
L->data[k] = L->data[k+1];//把刪除位置後的元素向前移動
}
L->length--;//線性表長度-1
}//end if
}//end if
}注:把元素向前移動的時候,從刪除位置i對應的下標i-1開始一直到表尾,然後把線性表的長度-1。
下面我們來分析一下線性表查詢插入刪除的時間複雜度。
查詢的時間複雜度
直接查詢到對應下標的資料,時間複雜度很明顯為O(1)。
插入和刪除的時間複雜度
最好的情況:插入和刪除的位置都在表尾,則不用進行元素的移動,時間複雜度為O(1)。
最壞的情況:插入和刪除的位置都在表首,則需要將整個表的元素向前移動或者向後西東,時間複雜度為O(n)。
平均的情況:插入和刪除需要移動n-i個元素,平均概率下,最終的移動次數就與最中間的元素的移動次數相等,為n-1/2 。根據上一章的大O階推導法,可得時間複雜度仍為O(n)。
最後來概括一下線性表的順序儲存結構的優缺點:
優點:
1.無須為表示表中元素之間的邏輯關係而增加額外的儲存空間(一開始就定義了最大的儲存空間)
2.可以快速地存取表中的任意位置的元素
缺點:
1.插入和刪除操作需要移動大量元素
2.當線性表長度變化較大時,難以確定儲存空間的容量
3.造成儲存空間的“碎片”(所謂碎片是指沒有用到的陣列空間)
今天就先到此為止啦,下班咯 ^ - ^ ————2016.7.29 18:00
下面給出測試程式碼:
//為了使結果顯而易見,將List輸出
void PrintList(SqList L){
cout<<"SqList: ";
for (int i =0; i< L.length; i++)
cout<<L.data[i] <<" ";
cout<<" length is "<<L.length<<endl;
}int main()
{
//線性表初始化
SqList L;
int n = 8;
for (int i =0; i< n; i++)
L.data[i] = i*i;
L.length = n;
PrintList(L);
//查詢第i個位置的元素
int e;
int i = 4;
GetElem(L,i,&e);
cout<<"get "<<i<<" is "<<e<<endl;
//在第i個位置插入e
i = 2;
e = 99;
ListInsert(&L,i, e);
cout<<"insert into "<<i<<" is "<<e<<endl;
PrintList(L);
//刪除第i個位置的元素
i = 3;
ListDelete(&L,i,&e);
cout<<"delete from "<<i<<" is "<<e<<endl;
PrintList(L);
return 0;
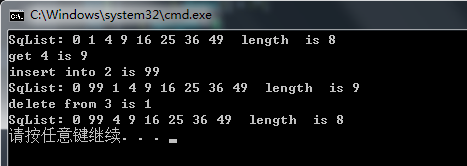
}下面給出測試程式碼的執行結果:
注:如果想下載完整程式碼的可以去我的資源頁下載。
二.線性表的鏈式儲存
首先我們需要知道一個名詞——結點,英文名Node,一個Node裡面包含了資料域和指標域,資料域用來儲存資料元素的資訊,指標域記憶體儲的資訊可以稱為指標或鏈,用來指示其直接後繼的資訊。
n個Node鏈結成一個連結串列,即為線性表的鏈式儲存結構,因為每個Node只包含一個指標域,又可以稱為單鏈表。
圖1是空連結串列,頭結點的後繼指標地址為null。
圖2是帶頭結點的單鏈表,其中頭結點的功能,以及和頭指標的區別我們會在下面仔細說明。一般使用線性表,都是指有頭結點的情況。
圖3是不帶頭結點的單鏈表。
頭指標:
1.線上性表的鏈式儲存結構中,頭指標是指連結串列指向第一個結點的指標,若連結串列有頭結點,則頭指標就是指向連結串列頭結點的指標。
2.頭指標具有標識作用,故常用頭指標冠以連結串列的名字。
3.無論連結串列是否為空,頭指標均不為空。頭指標是連結串列的必要元素。
頭結點:
1.頭結點是為了操作的統一與方便而設立的,放在第一個元素結點之前,其資料域一般無意義(當然有些情況下也可存放連結串列的長度、用做監視哨等等)。
2.有了頭結點後,對在第一個元素結點前插入結點和刪除第一個結點,其操作與對其它結點的操作統一了。
首元結點也就是第一個元素的結點,它是頭結點後邊的第一個結點。
3.頭結點不是連結串列所必需的。
加入頭結點有什麼好處呢?
加了頭結點之後,插入、刪除都是在後繼指標next上進行操作,不用動頭指標;
若不加頭結點的話,在第1個位置插入或者刪除第1個元素時,需要動的是頭指標。
例:在進行刪除操作時,L為頭指標,p指標指向被刪結點,q指標指向被刪結點的前驅,對於非空的單鏈表:
1.帶頭結點時
刪除第1個結點(q指向的是頭結點):q->next=p->next; free(p);
刪除第i個結點(i不等於1):q->next=p->next;free(p);
2.不帶頭結點時
刪除第1個結點時(q為空):L=p->next; free(p);
刪除第i個結點(i不等於1):q->next=p->next;free(p);
結論:帶頭結點時,不論刪除哪個位置上的結點,用到的程式碼都一樣;
不帶頭結點時,刪除第1個元素和刪除其它位置上的元素用到的程式碼不同,相對比較麻煩。
下面來看看鏈式儲存的結構程式碼:
typedef int ElemType; //ElemType 現定義為int
typedef struct Node{ //這個Node一定要寫
ElemType data; //儲存的資料
Node *next;//後繼指標
}Node;//別名為Node
typedef Node *LinkList; //定義LinkList注:data就是資料域,next就是指標域
下面就可以來看看基本的操作啦:
1.建立LinkList
//建立帶表頭結點的單鏈表 (從頭插入)
void CreateLsit(LinkList *L , int n){
LinkList p ;
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL ;//一個帶頭結點的單鏈表
for(int i = 0;i < n ; i++){
p = (LinkList) malloc (sizeof(Node));
p->data = i*i;
//從頭結點插入
p->next = (*L)->next;
(*L)->next = p;
}
}
思路:這個比較簡單,直接從頭結點插入就好了,插入的詳細操作在下面會講解。
//建立帶表頭結點的單鏈表(從尾插入)
void CreateLsit2(LinkList *L , int n){
LinkList p , r;
*L = (LinkList)malloc(sizeof(Node));
r = (*L);//尾指標等於頭指標
for(int i = 0;i < n ; i++){
p = (LinkList) malloc (sizeof(Node));
p->data = i*i;
//從尾部插入
r->next = p;
r = p;
}
r->next = NULL;//最後尾指標指向null
}思路:新建一個尾結點r,在開始的時候令r=(*L),插入的時候直接令r->next 等於新插入的結點p , 同時將r向後移動,在最後的時候令r->next = NULL;
2.查詢操作
//查詢LinkList中第i個數據
void GetElem(LinkList L,int i,ElemType *e){
LinkList p;
int j = 1;
p = L->next; //連結串列L指向的第一個結點
while( p && j < i){
p = p->next;
j++;
}//end while
if(!p || j > i){
//第i個元素為空,越界
}else{
*e = p->data;
}//end if
}思路:
1.建立一個新結點p,讓p指向連結串列的第一個結點,j作為當前位置,從1開始
2. 當p不為null,並且j<i時,遍歷連結串列,讓p的指標向後移動,j++
3. 如到連結串列末尾p為空,則說明第i個元素不存在
4. 否則,講結點的資料賦值給e
3.插入操作
//在第i個位置之前插入e
void ListInsert(LinkList *L , int i, ElemType e){
int j = 1;
LinkList p,s;
p = *L;
while(p && j < i){
p = p->next;
j++;
}
if(!p || j > i ){
//第i個位置,越界
}else{
s = (LinkList)malloc(sizeof(Node));
s->data = e;
s->next = p->next;
p->next = s;
}
} 思路:
1.建立一個新結點p,讓p指向連結串列的第一個結點,j作為當前位置,從1開始
2. 當p不為null,並且j<i時,遍歷連結串列,讓p的指標向後移動,j++
3. 如到連結串列末尾p為空,則說明第i個元素不存在
4. 否則,建立一個新結點s,將e賦值給s->data,然後就是單鏈表插入標準語句:s->next = p->next; p->next = s;
4.刪除操作
//刪除第i個元素
void ListDelete(LinkList *L , int i, ElemType *e){
int j = 1;
LinkList p,q;
p = *L;
while(p->next && j < i){
p = p->next;
j++;
}
if(!(p->next) || j > i ){
//第i個位置,越界
}else{
q = p->next; //q為臨時變數
p->next = q->next;
*e = q->data;
free(q);
}
} 思路:
1.建立一個新結點p,讓p指向連結串列的第一個結點,j作為當前位置,從1開始
2. 當p->next不為null,並且j<i時,遍歷連結串列,讓p的指標向後移動,j++
3. 如到連結串列末尾p為空,則說明第i個元素不存在
4. 否則,建立一個臨時結點q,令q=p->next,把q->data值賦給e,然後就是單鏈表刪除標準語句:p->next = q->next;最後把q結點用free釋放。
下面我們來分析一下線性表查詢插入刪除的時間複雜度。
查詢的時間複雜度
從頭結點開始找,一直到i位置結束,時間複雜度為O(n)。
插入和刪除的時間複雜度
從頭結點開始找,一直到i位置,再進行插入刪除操作,時間複雜度仍為O(n)。這樣看來,似乎鏈式儲存和順序儲存沒有在時間複雜度上沒有什麼區別。但如果我要在第i個位置同時插入多個元素,順序儲存每次的時間複雜度都是o(n),而鏈式儲存只有在查詢第i個位置的時候,時間複雜度為o(n),其餘的只需通過賦值和移動指標實現,時間複雜度都是o(1).
由此我們可得出結論:在刪除插入操作頻繁的時候,鏈式儲存的優勢就更明顯。
下面給出測試程式碼:
//輸出LinkList
void PrintList(LinkList L){
LinkList p = L->next;
cout<<"LinkList: ";
int j=0;
while (p){
cout<<p->data<<" ";
p=p->next;
j++;
}
cout<<" length is "<<j<<endl;
}int main(){
LinkList L,L1;
//從頭插入建立LinkList
CreateLsit(&L,10);
PrintList(L);
//從尾插入建立LinkList
CreateLsit2(&L1,10);
PrintList(L1);
//清楚表
ClearList(&L);
PrintList(L);
//插入
int i = 5;
int e = 99;
ListInsert(&L1,i,e);
cout<<"insert into "<<i<<" is "<<e<<endl;
PrintList(L1);
//查詢
GetElem(L1,i,&e);
cout<<"get "<<i<<" is "<<e<<endl;
//刪除
ListDelete(&L1,i,&e);
cout<<"delete from "<<i<<" is "<<e<<endl;
PrintList(L1);
return 0;
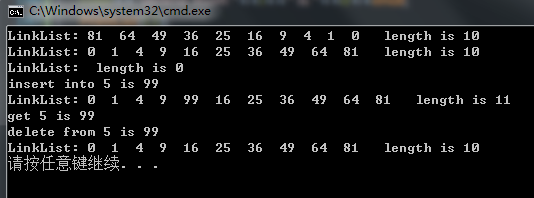
}下面給出測試程式碼的執行結果:
注:如果想下載完整程式碼的可以去我的資源頁下載。
Over ————2016.7.30 16:00