文章目錄

• 相機投影

相機投影

  本博文議題是影象形成過程，即三維世界的二維表示的形成，以及我們可以從中推斷出影象中出現的3D結構。

  從三維世界到二維影象的下降是我們失去一個維度的投影過程。 建模此過程的常用方法是通過中心投影(central projection)，其中來自空間點的光線從3D世界點通過空間中的固定點（投影中心）繪製。 該光線將與選擇作為影象平面的空間中的特定平面相交。 光線與影象平面的交點表示該點的影象。 如果3D結構位於平面上，則尺寸不會下降。

  該模型與相機的簡單模型一致，其中來自世界各點的光線穿過相機的鏡頭並照射在膠片或數字裝置上，產生該點的影象。 忽略焦點和鏡頭厚度等影響，合理的近似是所有光線都通過一個點，即鏡頭的中心。

  在將投影幾何應用於成像過程時，習慣上將世界建模為3D投影空間，等於$\rm IR^3$和無窮遠處的點。

  類似地，影象的模型是2D投影平面$\rm IP^2$。中心投影只是從$\rm IP^3$到$\rm IP^2$的對映。如果我們考慮用齊次座標$(\rm X,Y,Z,T)^T$寫的$\rm IP^3$中的點，並讓投影的中心是原點$(0,0,0,1)^T$，那麼我們看到的是固定的X，Y和Z的所有點$(\rm X,Y,Z,T)^T$，但是變化的T形成穿過投影的點中心的單個光線，因此全部對映到相同的點。因此，$($

  考慮到不同的投影中心和影象中的不同投影座標系，可以看出最一般的成像投影由秩為3的任意$3×4$矩陣表示，用於將在$\mathrm{I}$

  總之，投影相機對空間中的點的動作可以用齊次座標的線性對映表示

$\left( \begin{matrix} x \\ y \\ w \end{matrix} \right) =\rm P_{3\times 4} \left( \begin{matrix}\rm X \\ Y \\ Z \\ T \end{matrix}\right)$

  此外，如果所有點都位於一個平面上（我們可以選擇它作為平面 $\rm Z = 0$)，那麼線性對映會減少到

$\left( \begin{matrix} x \\ y \\ w \end{matrix} \right) = \rm H_{3\times 3} \left( \begin{matrix}\rm X \\ Y \\ T \end{matrix}\right)$

  這是一種射影變換。

相機作為點

  在中心投影中，$\rm IP^3$中的點被對映到$\rm IP^2$中的點，光線中的所有點穿過投影中心投射到影象中的相同點。

  出於影象投影的目的，可以將沿著這種光線的所有點視為相等。

  我們可以更進一步，並想象通過射影中心的光線代表影象點。因此，所有影象點的集合與通過相機中心的光線集相同。   如果我們通過它的前三個座標$(\rm X,Y,Z)^T$表示從$(0,0,0,1)^T$到點$(\rm X,Y,Z,T)^T$的光線，很容易對於任何常數$k$，光線$k(\rm X,Y,Z)^T$表示相同的光線。因此，光線本身由齊次座標表示。

  事實上，它們構成了二維光線空間。該組光線本身可以被認為是影象空間$\rm IP^2$的表示。

  在影象的這種表示中，所有重要的是相機中心，因為單獨確定形成影象的光線組。

  表示來自相同射影中心的影象形成的不同相機矩陣僅反映形成影象的一組光線的不同座標系。

  因此，從空間中的相同點拍攝的兩個影象是射影(projectively)等效的。

  只有當我們開始測量影象中的點時，才需要指定影象的特定座標系。只有這樣才有必要指定特定的相機矩陣。簡而言之，我們現在忽略的模視場（modulo field-of view），假定使用相同攝像機中心採集的所有影象都是等效的 - 它們可以通過射影變換相互對映，而無需任何關於3D點或攝像機中心位置的資訊。這些問題如圖1.1所示。

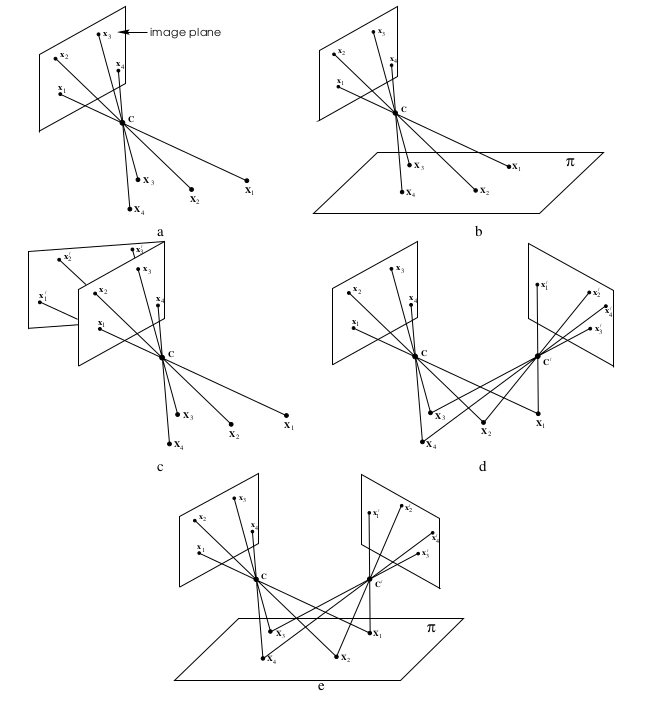
圖1 相機中心是必不可少的。 （a）影象形成：影象點$X_i$是平面與來自空間點$X_i$的光線通過相機中心C的交點。（b）如果空間點是共面的，則在世界和影象之間存在射影變換，${\mathbf {\rm x}_i} ={\rm H}_{3\times3}{\rm X}_i$ 。 （c）具有相同攝像機中心的所有影象通過射影變換相關，${\mathbf {\rm x'}_i} ={\rm H'}_{3\times3}{\rm X}_i$。 比較（b）和（c） - 在兩種情況下，都是通過中心的光線從一個平面對映到另一個平面。 在（b）中，對映在場景和影象平面之間，在（c）兩個影象平面之間。 （d）如果攝像機中心移動，那麼影象通常與射影變換無關，除非（e）所有空間點都是共面的。

校準相機

  為了充分理解影象與世界之間的歐幾里德關係，有必要表達它們的相對歐幾里德幾何。

  正如我們所看到的，3D世界的歐幾里德幾何是通過將$\mathcal{\rm IP}^2$中的特定平面指定為無窮遠處的平面,以及該平面中的特定二次曲線$\Omega$確定為絕對二次曲線來確定的。

  對於不在無窮遠平面上的攝像機，世界上無窮遠的平面一對一地對映到影象平面上。

  這是因為影象中的任何點都定義了空間中的光線，該光線在單個點中與無窮遠的平面相交。

  因此，世界上無窮遠的平面並沒有告訴我們關於影象的任何新內容。

  絕對二次曲線，無論是無窮遠平面上的二次曲線，都必須投影到影象中的二次曲線。 得到的影象曲線稱為絕對二次曲線的影象，或稱為IAC 。 如果影象中已知IAC的位置，則我們說相機已校準。

  在校準的相機中，可以確定從影象中的兩個點反投影的兩條光線之間的角度。我們已經看到，空間中兩條線之間的角度取決於它們相對於絕對二次曲線在無窮遠處與平面相交的位置。

  在校準的相機中，無窮遠處的平面和絕對二次曲線$\Omega_\infty$一對一地投影到影象平面和IAC上，表示為$\omega$。兩個影象點和$\omega$之間的投影關係恰好等於背投影光線與無窮遠平面的交點之間的關係，以及$\Omega_\infty$。因此，知道IAC，可以通過影象中的直接測量來測量光線之間的角度。因此，對於校準的相機，可以測量光線之間的角度，計算由影象塊表示的視場或確定影象中的橢圓是否向後投射到二次曲線。稍後，我們將看到它有助於我們確定重建場景的歐幾里德結構。

繪畫的3D重建

  使用射影幾何技術，在許多情況下可以從單個影象重建場景。 如果不對成像場景做出一些假設，就無法做到這一點。

通過單幅圖片重建一般是基於對場景結構的一些分析

   典型的技術涉及分析諸如平行線和消失點(vanishing points,也叫滅點)之類的特徵以確定場景的仿射結構，例如通過確定影象中觀察到的平面的無窮遠線。 關於在場景中觀察到的角度的知識（或假設），尤其是正交線或平面，可以用於將仿射重建升級為歐幾里德。

  這種技術尚不可能是全自動的。 然而，射影幾何知識可以構建到允許由使用者引導的場景的單檢視重建的系統中。

  這些技術已被用於重建從舊主繪畫衍生的3D紋理對映圖形模型。 從文藝復興時期開始，製作了具有極其準確視角的繪畫。 在下圖中，示出了從這樣的繪畫進行的重建。

圖2。 單檢視重建。 （a）原畫 - 聖傑羅姆在他的研究中，1630年，Hendrick van Steenwijck（1580-1649），Joseph R. Ritman私人收藏，荷蘭阿姆斯特丹。 （b）（c）（d）從繪畫中建立的3D模型的檢視。 數字由Antonio Criminisi提供。