Knuth-Morris-Pratt Algorithm(KMP演算法)探賾索隱(一)
KMP是指Donald Knuth、 Vaughan Pratt和James H. Morris三個演算法牛人的合併簡稱,Donald Knuth就是那個寫《計算機程式設計藝術》的ACM圖靈獎得主。這個演算法是在線性時間複雜度下完成字串匹配任務,這個演算法太牛逼了,簡潔優美但十分太晦澀,充滿技巧性,給大神跪了。
問題定義:
字串匹配問題:在文字串S中尋找模式串W(單詞串)的位置。對應程式語言就是:在(文字)字元陣列中S[]中尋找模式字元陣列W[]的起始索引m。
暴力解法:
很容易想到一個樸素解法,演算法複雜度為O(mn),就是遍歷整個文字字串,檢查每個字元與模式串的首字元是否相同,如果相同則繼續比對模式串後面的字母,直到所有模式串字母比對完,如果遇到不匹配則跳出迴圈從模式串首字母開始從頭檢驗。程式碼參考連結https://blog.csdn.net/To_be_to_thought/article/details/84679263
基本概念:
![]() 的字首是子串
的字首是子串![]() ,
,![]() ,且
,且![]() ,我們就說
,我們就說![]() 開始於
開始於![]()
![]() 的字尾是子串
的字尾是子串![]() ,
,![]() ,且
,且![]() ,我們就說
,我們就說![]() 結束於
結束於![]()
這裡的字首和字尾是嚴格字首和嚴格字尾,不包括原字串本身。字串的邊緣串(a border of x)是x的一個子串r,且![]()
![]() ),也就是說x的邊緣串既是x的字首串,又是x的字尾串,並且b是邊緣的長度。
),也就是說x的邊緣串既是x的字首串,又是x的字尾串,並且b是邊緣的長度。
例如:![]() 表示空串。
表示空串。
![]()
![]()
則x的邊緣串有![]() ,邊緣串
,邊緣串![]() 長度為0,邊緣串
長度為0,邊緣串![]() 長度為2。空串總是字串x的邊緣串,空串沒有邊緣串。在預處理階段,模式串的每個字首串的最長邊緣的長度是確定的。
長度為2。空串總是字串x的邊緣串,空串沒有邊緣串。在預處理階段,模式串的每個字首串的最長邊緣的長度是確定的。
重要定理:r和s都是字串x的邊緣串,並且r的長度小於s,則r也是s的邊緣串。
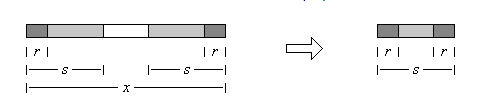
因此
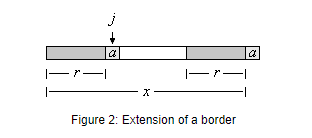
x為字串,a是字母表裡的一個字元,如果ra也是xa的邊緣串,x的一個邊緣串r可以通過a(一個字元)延伸。
下面舉個例子做做匹配實驗:
文字串S: ABC ABCDAB ABCDABCDABDE

模式串W: ABCDABD
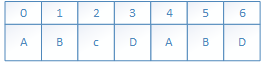
前三次比對如圖:

按照樸素的思想應該進行如下調整再比對:
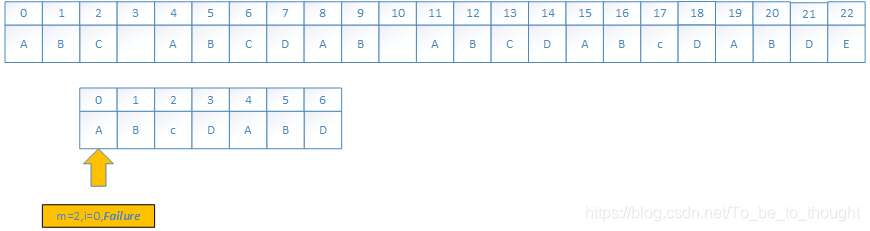


再轉到下一步:

但因為已經比對過S[8]和S[9]的資訊,可以利用這個資訊直接將新的比對任務的起點移到如下圖:

當S[10]和W[2]發生失配時,直接將新的比對任務移動到S[11],下圖:

當S[17]和W[6]發生失配時,直接將新的比對任務移動到S[15],如下圖:
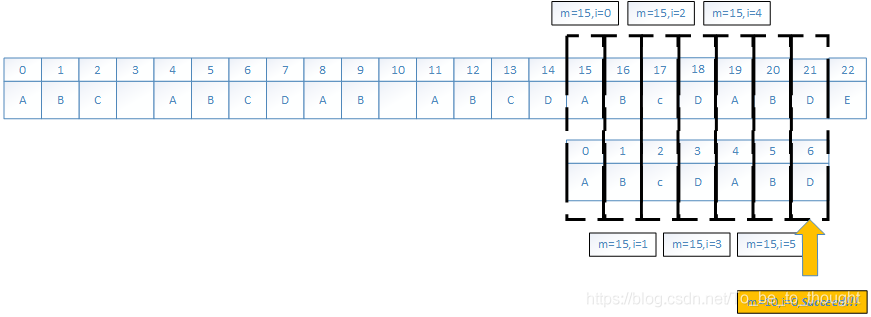
按照以時間換空間的思想,應該在失配時將字串的資訊記錄下來,下面來看看next陣列到底存的是什麼資訊?
我們現在假設存在部分匹配表(partial match table)陣列T[],這個表用於告訴我們:當前匹配失敗時如何尋找預匹配起點。如果有一個以S[m]為起點(S[m+k-1])的比對任務在S[m+i]和W[i]失配時,下一個可能的比對任務可能以S[m+i-T[i]]為起點,尤其是下一個可能的位置一定在比m大的索引上(因為T[i]<i),並且我們不需要檢驗S[m+i-T[i]]到S[m+i-1]的字串是否相等,因為T[i]表明:在模式串中W[0:i-1]組成的子串的字首和字尾最長公共串長度為T[i]。
舉個例子:

下面把這個例子構造部分匹配表的演算法流程描述一下(如圖):
| i |
j |
j |
… |
… |
i |
j |
b[i] |
| 0 |
-1 |
|
|
|
0 |
|
-1 |
| 0 |
-1 |
|
|
|
1 |
0 |
0 |
| 1 |
0 |
-1 |
|
|
2 |
0 |
0 |
| 2 |
0 |
|
|
|
3 |
1 |
1 |
| 3 |
1 |
|
|
|
4 |
2 |
2 |
| 4 |
2 |
|
|
|
5 |
3 |
3 |
| 5 |
3 |
1 |
0 |
|
6 |
1 |
1 |
演算法開始 :i=0,j=-1,b[i=0]=-1
i=0<6,(j=-1<0不符合內迴圈條件) j=0,i=1,b[i=1]=j=0
i=1< 6,(j = 0, p[i] != p[j]) j = b[0] = -1 (j=-1<0跳出迴圈) i=2 , j=0 b[2]=j=0
i=2<6 ( j=0>=0 , p[2]=p[0] 跳出迴圈) i=3,j=1,b[3]=j=1
i=3<6, (j=1,p[i=3]=p[j=1]跳出迴圈) i=4 , j=2 , b[i=4]=j=2
i=4<6 , (j=2>=0, p[i=4]=p[j=2] 跳出迴圈) i= 5, j=3, b[i=5]=j= 3
i=5<6 (j=3>=0,p[i=5]=!p[j=3] ) j=b[j=3]=1 (j=1>=0,p[i=5]!=p[j=1] ) j=b[j=1]=0 (j=0>=0,p[i=5]=p[j=0]跳出迴圈) i=6, j=1 , b[i=6]=1
i=6結束迴圈
在進行運算時我們發現這個b[i=0]=-1的-1設定的恰到好處,會比b[0]=0好很多!!!
下篇敬請期待!!!
參考文獻:
https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm
http://www.inf.fh-flensburg.de/lang/algorithmen/pattern/kmpen.htm
