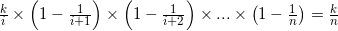給定一個單鏈表，隨機選擇連結串列的一個節點，並返回相應的節點值。保證每個節點被選的概率一樣。

進階: 如果連結串列十分大且長度未知，如何解決這個問題？你能否使用常數級空間複雜度實現？

示例:

// 初始化一個單鏈表 [1,2,3].
ListNode head = new ListNode(1);
head.next = new ListNode(2);
head.next.next = new ListNode(3);
Solution solution = new Solution(head);

// getRandom()方法應隨機返回1,2,3中的一個，保證每個元素被返回的概率相等。
solution.getRandom();

思路：首先這道題的限定是：水庫抽樣Reservoir Sampling，水庫抽樣的原理是在原資料集很大的情況下比如n，但是我們事先不知道n，求從中取k個數且保證每個數的取得概率相同，均為k/n。

方法：初始化陣列長度為k，對於前k個數，放入陣列不做處理。

           對於第k+1個數，需要與陣列中某個數（假設為x）交換的概率為k/(k+1)，那麼可以證明對每個數直到處理到n個數，每個數仍然在陣列中的概率相同，均為k/n。

          假設以第i個數為例，第i個數第i次放入陣列的概率為k/i，對於數i+1，第i個數不被換出的情況等於=（1-第i個數被換出來的概率）=（1-（第i+1個數的取得概率隨機替換）*第i個數被選擇的概率）=（1-k/(i+1)*(1/k)）=1-1/(i+1)，同理第i+2個數進來也是這麼分析，直到第n個數，所以第i個數最後依然在陣列中的概率為：

具體分析：對於這道題，我們取k=1，n為不知道的大數。那麼我們的思路如下：

Init : a reservoir with the size： k
 
for i= k+1 to N        //k=1
 
    M=random(1, i);
 
    if( M < k)
 
     SWAP the Mth value and ith value
 
end for

參考程式碼：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
	/** @param head The linked list's head.
		Note that the head is guaranteed to be not null, so it contains at least one node. */
	Solution(ListNode* head) {
		this->head = head;
	}

	/** Returns a random node's value. */
	int getRandom() {
		int res = head->val;
		ListNode* next = head->next;
		int i = 2;
		while (next) {
			int div = rand() % i;
			if (div == 0) res = next->val;
			i++;
			next = next->next;
		}
		return res;
	}
private:
	ListNode* head;
};

/**
 * Your Solution object will be instantiated and called as such:
 * Solution obj = new Solution(head);
 * int param_1 = obj.getRandom();
 */