半導體隨機儲存器晶片內整合有記憶功能的儲存矩陣，譯碼驅動電路和讀/寫電路等等。 下面介紹幾個重要的概念： 讀寫電路：包括讀出放大器和寫入電路，用來完成讀/寫操作。 地址線：單向輸入，其位數與晶片的容量有關 片選線：確定哪個晶片被選中（用來選擇晶片） 資料線：雙向輸入，其位數與晶片可讀出或者寫入的位數有關，也與晶片容量有關。

儲存容量

通常我們將儲存容量表示為： 字數 X 位數，比如 64K X8位，其含義為，以8位構成一個字，一共有64個字。這個概念要相當熟悉，後面理解題目很有用。 下面我們來看一道例題：

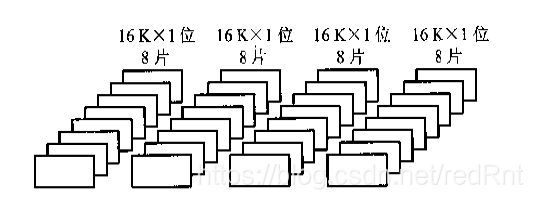
一個64K x 8位的儲存器，可以由（）個16k x1位的儲存晶片構成？

分析：64K x 8位，說明該儲存器是以8位構成一個字，因此，每讀出一個字，需要選中8片16k x1位的儲存晶片，而一片能表示16k，因此一共需要64/16 = 4片，根據組合的原理，一共需要4x8 = 32片。

半導體隨機存取器，習慣上多稱為RAM，按其儲存資訊原理不同，可以分為靜態RAM（SRAM）和動態RAM（DRAM）。

SRAM

SRAM儲存原件所使用的mos管多，佔用矽片面積大，整合度低，但是採用觸發器工作原理儲存資訊，因此即使資訊讀出之後，它仍然保持原狀，不需要再生，但是電源掉電時，原存有的資訊就會消失，因此它屬於易失性儲存器。因為這個比較的簡單，因此就簡單介紹一下就好： 工作原理：觸發器 優點：

1. 能長久儲存資訊
2. 速度快，工作穩定
3. 無需重新整理
4. 無需讀後再生

缺點：功耗大，整合度低，價格高。 典型應用：cache

DRAM（這個是重點）

與SDRAM相比，DRAM所用的mos管少，佔矽面積小，因而功耗小，整合度高但是因為採用了電容儲存電荷的原理來寄存資訊，會發生漏電現象，所以要保持狀態不變，需要定時重新整理，因為讀操作會使得狀態發生改變，故需要讀後再生。且速度比SRAM慢。但是由於其功耗小，整合度高，被廣泛應用於計算機中。 典型應用：主存

儲存記憶原理（瞭解）

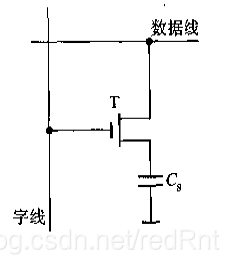定義：存“0”：C中沒有電荷，存“1”：C中有電荷 讀入的時候，T中的高電平使得T通導，如果此時C有電荷，那麼資料線就會產生電流，視為讀出1.否則視為讀出0 寫入的時候，若為高電平，則經過T對C充電，充電後有電荷，於是存1，若為低電平，C經過T時放電，C中沒有電荷，於是存0.

DRAM的重新整理

問：為什麼要對DRAM進行重新整理？如何進行重新整理？ 由於動態儲存器的原理是容儲存電荷的原理，且訪問儲存單元是隨機的，有可能某些儲存單元長期得不到訪問，其儲存單元內原資訊就會慢慢消失（原因）。重新整理的過程實質上是將原資訊讀出，再由重新整理放大器形成原資訊並重新寫入的再生過程，稱為讀後再生。 下面介紹一下重新整理過程中要用到的名詞。

• 重新整理週期：在規定的時間內，對DRAM全部基本單元進行一次重新整理（即兩次重新整理之間的相隔時間），一般為ms級別，2ms。
• 死時間：重新整理時，某段時間需要暫停讀寫操作，這段時間由於外界不能對儲存器進行操作，因此稱為死時間。
• 存取週期：DRAM完成一次讀寫操作所需要的最短時間
• 死時間率：

DRAM常見的重新整理方式有三種：集中重新整理，分散重新整理，非同步重新整理 重新整理的過程為：以行為單位，讀出一行中全部單元的資料嗎，經過訊號放大後，同時寫回。讀出時候一定斷開儲存器的輸出。

集中重新整理

做法：在重新整理週期內，對全部儲存單元集中一段時間進行重新整理（逐行進行），此時必須停止讀寫操作。 看看下面的例題：

設對128 x 128矩陣的儲存晶片進行重新整理，若存取週期為0.5us，重新整理週期為2ms，採用集中重新整理的方式，那麼對128行集中重新整理，一共需要（）us？死時間率為（）%？

分析：重新整理一遍的時間 = 存取週期 x行數，於是可以求得重新整理時間。在重新整理時間內，不能進行讀寫操作，因此死時間就是重新整理的那段時間，佔用的存取週期數值上等於行數。利用計算公式算出死時間率為32.%。所以很容易得到： 但是這種做法有個極其不好的缺點：對於經常要進行讀入讀出的程式，要陷入大量的等待時間，CPU的工作效率不高。

分散重新整理

做法：對每行儲存單元的重新整理分佈到每個存取週期內完成，其中吧機器的存取週期（記為tc），分成兩個部分，前半段的tm用來記錄讀寫，後半段（tr）用來重新整理，即tc = tm +tr。如圖：

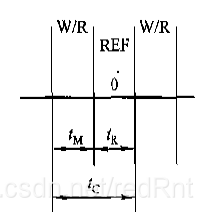
若讀寫週期 tc = 0.5us ，那麼存取週期tc = （0.5+0.5）us = 1us 現在沿用上面的題目：

設對128 x 128矩陣的儲存晶片進行重新整理，若存取週期為1us，重新整理週期為2ms，採用分散重新整理的方式，那麼對128行分散重新整理，一共需要（）us？死時間率為（）%？

分析：因為在讀寫操作之後，立刻重新整理，那麼每讀取操作一次，就會重新整理一次，重新整理128行就需要 1us x 128 = 128 us。由於重新整理是在讀寫操作過後直接完成的，所以不存在死時間。也就是死時間率為0. 缺點：這樣無異於加長了存取週期，會使系統執行速度降低，重新整理操作也過於頻繁。

非同步重新整理

做法：在重新整理週期內對所有行各重新整理一次，即每隔（重新整理週期/總行數）us，重新整理一次。這種方式是前面兩種方式的結合，既能縮短死時間，又能充分利用重新整理週期，提高重新整理頻率。 題目同上：

設對128 x 128矩陣的儲存晶片進行重新整理，若存取週期為0.5us，重新整理週期為2ms，採用非同步重新整理的方式，那麼對128行非同步重新整理，一共需要（）us？死時間率為（）%？

每隔（2ms/128） = 15.6us重新整理一次，每一次重新整理，死時間都是存取週期內的時間為0.5us，對於該行來說，下一次輪到它重新整理還是間隔了2ms，所以死時間率為 1/4000.(2ms 裡面有4000個存取週期)。所以; 1/4000 << 3.2% 若將DRAM的非同步重新整理安排在CPU對指令的譯碼階段（此階段CPU訪問儲存器），那麼也就不存在死區。