一、多項式加法運算

那麼，在計算機中是如何實現的呢？ 採用不帶頭結點的單向連結串列，按照指數遞減的順序排列各項

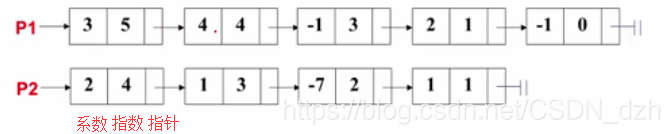
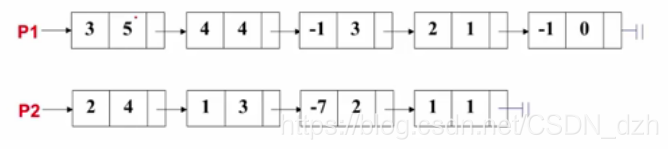
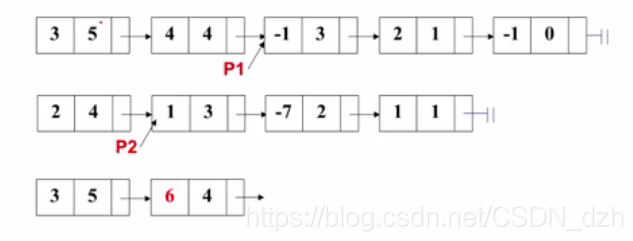
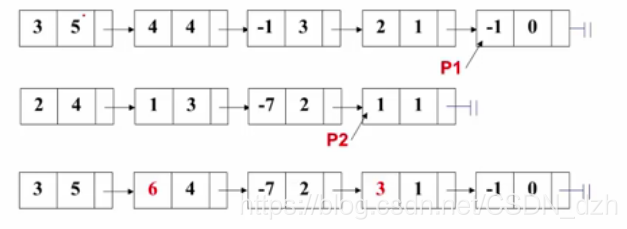
1. 演算法思路 兩個指標p1和p2分別指向這兩個多項式第一個結點，不斷迴圈：

• p1->expon == p2->expon : 係數相加，若結果不為0，則作為結果多項式對應項的係數。同時p1和p2部分分別指向下一項
• p1->expon > p2->expon : 將p1的當前項存入結果多項式，並使p1指向下一項
• p1->expon < p2->expon : 將p2的當前項存入結果多項式，並使p2指向下一項 當某一多項式處理完時，將另一個多項式的所有結點依次複製到結果多項式中去。
  

void Attach(int c, int e, Polynomial *pRear) {
	Polynomial P;
	P = (Polynomial)malloc(sizeof(struct PolyNode));
	P->coef = c;	// 對新結點賦值
	P->expon = e;
	P->link = NULL;
	(*pRear)->link = P;
	*pRear = P;		// 修改pRear值
}

Polynomial PolyAdd(Polynomial p1, Polynomial p2) {
	Polynomial front,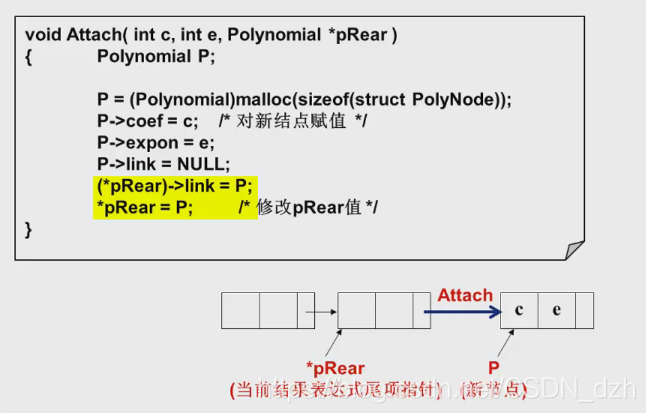
 
 rear, temp;
	int sum;
	rear = (Polynomial)malloc(sizeof(struct PolyNode));
	front = rear;		// 由front記錄結果多項式連結串列頭結點
	while (p1 && p2) {	// 當兩個多項式都有非零項待處理時
		switch (Compare(p1->expon, p2->expon)) {
		case 1:
			Attach(p1->coef, p1->expon, &rear);
			p1 = p1->link;
			break;
		case
 
 -1:
			Attach(p2->coef, p2->expon, &rear);
			p2 = p2->link;
			break;
		case 0:
			sum = p1->coef + p2->coef;
			if (sum)
				Attach(sum, p1->expon, &rear);
			p1 = p1->link;
			p2 = p2->link;
			break;	
		}
	}
	// 將未處理完的另一個多項式的所有結點依次複製到結果多項式中去
	for (; p1; p1 = p1->link){
		Attach(p1->coef, p1->expon, &rear);
	}
	for (; p2; p2 = p2->link){
		Attach(p2->coef, p2->expon, &rear);
	}
	rear->link = NULL;
	temp = front;
	front = front->link;	// 令front指向結果多項式的第一個非零項
	free(temp);
	return front;
}

二、多項式的乘法和加法運算

求解思路：

1. 多項式表示

• 資料結構設計 其中連結串列的頭用p1來指向這個結點，然後每個結點都有一個指標指向下一個結點，每個結點裡面都包含兩個關鍵的資訊，就是係數和指數

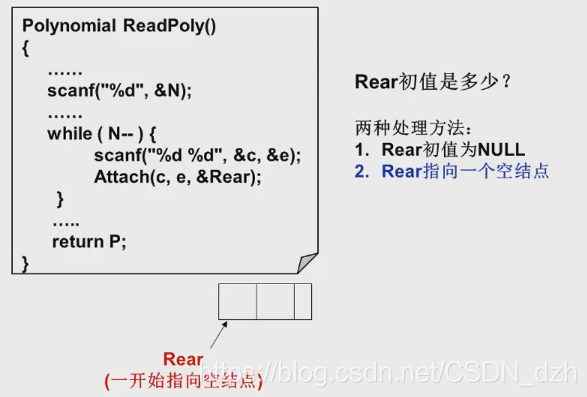
2. 程式框架
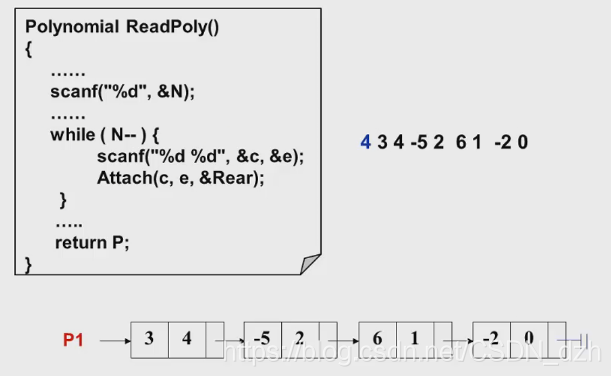
3. 讀多項式 Attach函式已在上面給出
4. 加法實現
5. 乘法實現
6. 多項式輸出